
Weekend Mathematics/コロキウム室/NO.119
| NO.1006 | 2001.8.16. | yokodon | 恒等式の解き方(2) |
数値代入法と係数比較法ですが、どちらでも良いのではないかと思います。
整式の場合は、高々2次までならどちらでやっても大差ないのではないかと思いま
す(ある程度習熟した者の見解かも知れませんが;尤も、未習者相手の教育現場では
そうとばかりも言ってはいられないことは重々承知しておりまして、上記の「大差な
いのではないか」は、あくまで教育上の配慮を多少度外視した数学的見地からの考え
です)。
ご紹介の例題の場合、[2][3][4]の各式は“全ての実数 x,y に関して[1]
が成り立つための必要条件”です。
“全ての実数 x,y に関して[1]が成り立つ”ならば“ある実数 x,y に対して[1
]が成り立つ”ことが必要であるという論理のもとで、3つの式が導かれているわけ
です。3元2次連立方程式の解として求まる(a,b,c)の値の組は、くだんの必要条
件であり、従って、十分性の確認を i) および ii) で行っているわけです。
#『逆は必ずしも真ならず』の典型例と言って良いのではないでしょうか?
求まった答え“(a,b,c)=(-5,-1,1)”は、“全ての実数 x,y に関して[1]が
成り立つための必要十分条件”ということになります。この“必要条件、十分条件と
いう単語をきちんと使う”という方針で、如何でしょうか?
数値代入法は「必要性と十分性を分けて考えるやり方」、係数比較法は「必要十分
条件をいっぺんに求めるやり方(大仰に『同値変形』と言っても良いでしょう)」と
いうことで、数学でよく言われる『同じ結論を違う見地から導く』ことの出来る具体
例と見ることが出来るのではないでしょうか。よって、“どちらでも良い”と結論致
したいと思います。
蛇足。平面上や空間上の点の軌跡及び線分・曲線の掃過領域を求める問題や、微分
の応用で関数の極値や変曲点の判定をする問題などでも、議論の逆をたどることや命
題の必要性・十分性の考察を求められる問題は多々ありますよね?(例えば、動くパ
ラメータを含む2直線の交点の軌跡や、3次関数が極値を持つための係数に関する条
件など)

| NO.1007 | 2001.8.18. | 8305 | 標準偏差(1) |
仕事で「標準偏差値」という言葉が出てきたのですがこの計算式がわからず、
相手の方に聞く事もできずに悩んでいます。

| NO.1008 | 2001.8.18. | Junko | 標準偏差(2) |
例えば、1クラス分の数学のテストの点など、ばらつきのあるデータを分析する際
に、そのばらつき具合をはかる尺度として、「標準偏差」という概念があります。
実際の計算には、まず平均値を求める必要があります。
これは普通の算術平均です。これをmとします。
各データとmとの差をとり、これを2乗し、これの平均値をとります。
これを分散(s2)といいます。
そしてこれの平方根sが、標準偏差となります。
例えば、3,6,4,5,8,9,10,4,5,6という10個のデータがあった
とします。
平均は6.0となります。
各データと平均値m=6との差は、
3,0,2,1,2,3,4,2,1,0となります。(プラスマイナス関係ありま
せん、次に2乗が控えていますから)
各データを2乗します。
9,0,4,1,4,9,16,4,1,0です。
これの平均値が、4.8になります。(これが分散)
そしてこれの平方根約2.2が標準偏差となります。
| xi | 3 | 6 | 4 | 5 | 8 | 9 | 10 | 4 | 5 | 6 |
|---|---|---|---|---|---|---|---|---|---|---|
| |xi-m| | 3 | 0 | 2 | 1 | 2 | 3 | 4 | 2 | 1 | 0 |
| |xi-m|2 | 9 | 0 | 4 | 1 | 4 | 9 | 16 | 4 | 1 | 0 |
因みに、平均ちょうどが偏差値50というのはご存知ですよね?
平均+標準偏差のデータが偏差値60、平均-標準偏差のデータが偏差値40です。
平均+標準偏差×2のデータが偏差値70、平均-標準偏差×2のデータが偏差値30です。
「標準偏差」ということばの持つ意味がおわかりいただけたでしょうか?
EXCEl等のソフトが使える状態でしたら、EXCELの関数で簡単に求めることもできます
ので、やってみてください。

| NO.1009 | 2001.8.20. | DDT | 微分(3) |
微分 その3(1行のはずだったテーラーの定理の証明と、強引なオチ)
まず平均値の定理です。
「その1」より、関数の1点の内部には直線が住んでるらしいということの、
有限の大きさでの正当化は、平均値の定理だと思えます。並べて書くと、
f(x+h0)=f(x)+h0・f'(x)
(h0→0で無限小の場合: 1点の内部)
f(x+h0)~f(x)+h0・f'(x)
(h0~0で有限の場合 : 1点まわりの線形化 = 1次のテーラー近似)
f(x+h0)=f(x)+h0・f'(x+h1) となる、0<|h1|<|h0|がある.
(h0が任意有限の場合 : 上記2モデルの数学的正当化で、平均値の定理)
この対応がもし正しいとすると、「その2」よりn次のテーラー級数は
n階の後退差分から曲がりなりにも得られるのですから、
それはn点まわりのn回の線形化に対応するはずであると信じ込みました。
よってn次のテーラーの定理は、平均値の定理をn回繰り返し使って証明すべきだという、
強迫観念に取り憑かれました。実際にやってみると次のようになります。
| f(x+h0) | =f(x)+h0・f(1)(x+h1) | となる0<|h1|<|h0|がある |
| =f(x)+h0・f(1)(x)+h0h1・f(2)(x+h2) | となる0<|h2|<|h1|<|h0|がある | |
| =f(x)+h0・f(1)(x)+h0h1・f(2)(x)+h0h1h2・f(3)(x+h3) | となる0<|h3|<|h2|<|h1|<|h0|がある | |
| ・・・ |
コーシーの平均値定理
関数fとg:R → Rが、閉区間[x,x+h0]で連続,
開区間(x,x+h0)で微分可能で、
g(x)=g(x+h0) かつ g(1)(x)=0ならば、
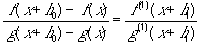
となる0<|h1|<|h0|が存在する。
ここでh(j)は、h:R → Rのj階微分を表す。
[証明]
X=g(x),Y=f(x)とパラメータ表示された関数Y=F(X)に対する平均値の定理と考えれば、
ふつうと同じに証明できる。定理の成立条件は、
通常の平均値の定理,テーラーの定理の成立条件と同等.
[証明終わり]
テーラーの定理は、ここから系として得られます。
要するに最初から、テーラー級数の形を、仮定してやればよかったのです。
「その1」「その2」で述べた経過で、曲がりなりにもテーラー級数の形は導けたので、
テーラー級数の形を最初から仮定することは、自分に対して一応許せました。
いきなりですが、オチを準備するため、急にフォントが小さくなります。
系-1(テーラーの定理)
関数f:R → Rが、閉区間[x,x+h0]でCn級,開区間(x,x+h0)で(n+1)回微分可能とする。
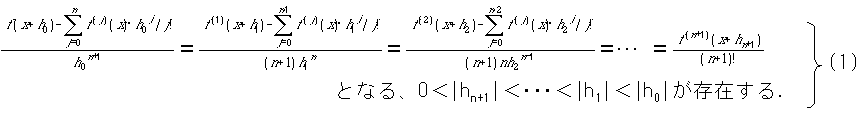
[証明]
式(1)の初項(左端)から、コーシーの平均値定理を(n+1)回繰り返し使えば、式(1)が得られる。
式(1)の初項と末項を直接等置すれば、テーラーの定理.
[証明終わり]
間違いではないと思うのですが、系-1に気づいた時に、
それが余りに自分の望み通りの証明だったので、すっかり嬉しくなってしまい、
テスト準備もどこえやら、呑みにでかけ、テストでは討ち死にしかけました。
ともあれ、次の副産物が得られます。
系-2
上記点列{|hn|}は、0<|hn|<・・・<|h1|<|h0|で
下に有界な減少列なので収束する.
そして次のことは言えそうです。
予想
関数f:R → Rが、適当な区間A⊂Rでテーラー展開可能ならば、lim(n→∞) |hn|=0.
log(1+x)のテーラー展開については、予想を確認したことがありますが、
一般の場合は未確認です。ところでオチです。
今回テーラーの定理を証明するために、昔のノートやテキスト
をあらためてひっくり返してみましたが、標準的なテーラーの定理の証明はどれもみな、
本当に1行で済んでいて本当にあせってしまいました。
それに対して式(1)の本当の実質は、本当にn行分です。
それが1行に見えるのは、フォントが小さいせいと、
省略記法・・・のせいでした。というわけで、強引なオチをつけたところで、
終わりにしたいと思います。

| NO.1010 | 2001.8.21. | BossF | 誕生日(3) |
問題2,4について
まず、N人いて誕生日が重なったり連続しない場合の数を考えに行きます。
番号がついたN個の●(これがN人の誕生日)と
366-N個の区別できない○(その他の日)の並べ方として考えます。
まず、●○のペアをN個作り、そのペアと残りの○366-2N個の順列の総数は
(366-2N+N)!/(366-2N)!=(366-N)!/(366-2N)!…①
これが大晦日生がいない場合の数です。
そこで、大晦日に●(すなわち元旦は○)の場合の数を考えます。
残りを①と同様に並べると
{364-(N-1)}!/{364-2(N-1)}!=(365-N)!/(366-2N)!…②
| ①+② | ={(366-N)!+(365-N)!}/(366-2N)! |
| =(367-N)(365-N)!/(366-2N)! | |
| =(367-N)(365-N)(364-N)…(366-2N+1)…③ |
| 1-350・348・347・346…333/366^17 | |
| = | 1-(350/366)(348/366)(347/366)…(333/366) |
| = | 0.699… |

| NO.1011 | 2001.8.21. | yokodon | 微分(4) (8/22,1:00一部修正) |
f(x+h0) の展開式で、数列{hn}を以下を満たすようにとります。
hn=h0/(n+1) n=1,2,...
このとき、
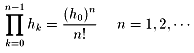
となって、形式的にはテーラー展開の式が出てきますね。
且つこのとき、数列{|hn|}は、狭義単調減少且つ下に有界です
(但し、h0 が0 でないとき)。
但し、この様にとった{hn}が、コーシーの平均値定理を満たすかどうかは別途
確認が必要でしょうけれど。
ただ、コーシーの平均値定理の反復で得られる各等式にそって、各々の |hn| を
順次上から押さえていくと、上記の形式的議論もあながちウソとは言えなさそうです。
既にご存じかも知れませんが、テーラー展開の式を導くだけなら、微分積分学基本
定理の反復で可能です。
実数 a,b(a<b とします)と任意の自然数 n に対して、実数上の関数 f が以下
を満たすものとします。
「区間 (a,b) 上で、f(n);n 次導関数…は連続且つ微分可能」
このとき、ある c ∈(a,b) とある r(≧0)が存在して、c-r ≦ x ≦ c+r なる x
において、以下の計算が可能です。
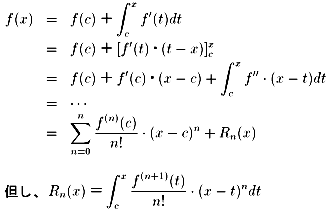
この形になることは、数学的帰納法を用いて示すことが出来ます。
そして、n →∞ で Rn →0 になれば、最右辺の級数は収束して、おなじみの形の
式を得ます。
r の値は、例えば以下のようにして求めることが出来ます。証明は、無限級数の収
束に関するダランベール条件から直ちに得られます(r の値には、0 や無限大も許す
ことにします)。
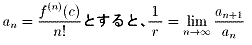
数学的な論理構成が微妙に不正確かも知れませんが、「曲線の中に直線が住んでい
る」という趣旨と著しくは反れないと思いますし、DDTさんの仰ることと上記とは
本質的に同じだろうと思います。

| NO.1012 | 2001.8.21. | Junko | 誕生日(4) |
問題1:17人いて,誕生日が同じ人が少なくとも1組いる確率は
1-366P17/36617ということで、
EXCELで計算してみたら、以下のようになりました。
=1-PERMUT(366,17)/366^17=0.3142882141・・・

| NO.1013 | 2001.8.21. | 水の流れ | 正七角形2(1) |
太郎さんは、第78回の応募問題の中で、正七角形の異なる2本の対角線の長さに、
次のような性質があることに気がつきました。
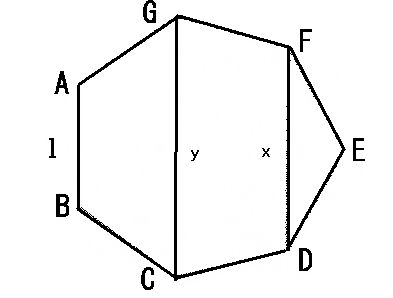
一辺の長さが1の正七角形ABCDEFGがあります。
図の中にある2つの対角線DFとCGの長さをxcm、ycmとするとき、
(y+x)2(y-x)=x2y が成り立つことを示してください。

| NO.1014 | 2001.8.22. | Junko | 正七角形2(2) |
第78回の応募問題の結果より、
1/x+1/y=1、つまり x+y=xy
証明すべき式「(y+x)2(y-x)=x2y」の両辺をx+y=xy>0で
割ることによって得られる、
「(y+x)(y-x)=x」を証明します。
第78回の応募問題の解答の中で、「水の流れ」
さんが解かれた方法でアプローチします。
つまり、半径Rの円に内接する正七角形を作り、1辺が1の中心角を2θとおく。
(ここで、θ=180゜/7 となる。)
すると、Rsin θ=1/2 ,x=2Rsin 2θ,y=2Rsin 3θとなります。
| (y+x)(y-x) | =2R(sin 3θ+sin 2θ)・2R(sin 3θ-sin 2θ) |
| =(2R)2・2sin(5/2)θcos(1/2)θ・2cos(5/2)θsin(1/2)θ | |
| =(2R)2・2sin(5/2)θcos(5/2)θ・2cos(1/2)θsin(1/2)θ | |
| =(2R)2・sin5θ・sinθ | |
| =2Rsin5θ・2Rsinθ | |
| =2Rsin2θ・2Rsinθ・・・(7θ=πより) | |
| =x・1 | |
| =x |
これは図形的には、どんな意味を持つのでしょうか?

 E-mail
E-mail
 戻る
戻る