Weekend Mathematics／コロキウム室／NO.107
| NO.911 | 2001.1.1. | Junko | 謹賀新年 |
あけましておめでとうございます。
今日から２１世紀、どんな時代になるのでしょうか？
こどもたちの将来が幸せなものであってほしいと願っています。
| NO.912 | 2001.1.5. | Junko | 箱の問題・その後（１） |
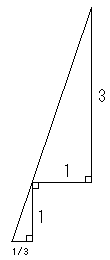
NO.48 箱の問題の発展問題で、
（３）３等分点を作る方法です。
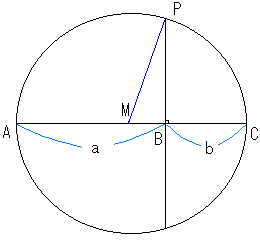
右の図をみてください。
基準になる長さを１とします。
直角をはさんで２辺の長さが１と３の直角三角形を作ります。
それを縮小した形で、1/3 という長さを得るわけです。
このやり方を拡張すれば、任意の自然数ｎに対して、
1/n という長さを作図することができると思います。
| NO.913 | 2001.1.6. | Chikako | ボ−ルの問題・その後（１） |
実は、先日友人から出された問題がずっと
解けずにいます。
問題というのは、 NO.11 ボ−ルの問題
によく似ているのですが、
「12個のボールがあって、その中の一つだけ、他のものと
重さが違います。（軽いか重いかわかりません。）天秤を3回だけ
使ってどれが違うのか見つけてください」
というものなのです。
NO.11 ボ−ルの問題では9個のバージョンでしたが、
12個でも3回で出来るものなのでしょうか？？？
| NO.914 | 2001.1.6. | Junko | 箱の問題・その後（２） |
NO.48 箱の問題の発展問題の
（１）
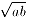を作図する方法について、
日本評論社の「数学１００の発見」から引用します。
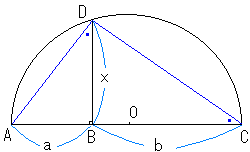
右の図のように、辺ACの中点Oを求め、そこを中心に半径がOAとなるような円を描きます。
点Bを通り、ACに垂直な辺が円と交わる点をDとします。
BD＝x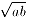＝となります。
なぜなら△ABDと△DBCが相似であることから、ab＝x２となるからです。
| NO.915 | 2001.1.7. | 高橋 道広 | 箱の問題・その後（３） |
NO.48 箱の問題の発展問題の
（１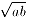）を作図する方法について私が考えたのは
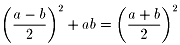
つまり、三平方の定理を使うことによって、求まるかなあと思ったものですが…
作り方は、次の通りです。（a>bとします）
一直線上にAB=a、BC=bとなる点ABCを取ります。ACの中点を求めてMとします。
MB=MC-BC=(a+b)/2-b=(a-b)/2
次に、Bを通るACに垂直な直線を引き、Mを中心に
半径MCで円を描き、交点をPとします。
すると、MP=(a+b)/2となり、三角形MBPで、上
に書いた三平方の定理が成立して、BP=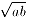となります。
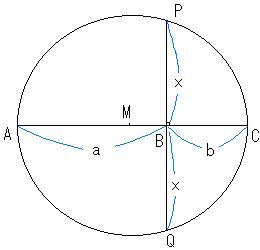
しかし、円を使ったほうが簡単ですね。
一直線上にAB=a、BC=bとなる点ABCを取ります。
ACの中点を求めてMとします。
Mを中心に、半径AMで円を描きます。
Bを通りACに垂直な直線とこの円の交点を
P,QとするとBP=BQ=Xとおけば、方べきの定理から、x2=ab
注）方べきの定理については、NO.44 ハスの問題へ
| NO.916 | 2001.1.7. | Junko | お年玉（２） |
子供がｎ人のときの分配方法をＰ(ｎ)通りとします。
子供が１人のときは、一万円か、五千円か、二千円か、もちろん３通りです。
Ｐ(１)＝３
子供が２人のときは、２人とも一万円か、五千円か、二千円の３通り。
または２人の内容が異なる場合は、その組み合わせが３Ｃ２＝３通りで、それぞれ分配の仕方が２通りだから、３×２＝６通り。
両者の合計で、Ｐ(２)＝９
これはちょうど、(ｘ＋ｙ＋ｚ)２の展開式を連想させます。
つまり、(ｘ＋ｙ＋ｚ)２＝ｘ２＋ｙ２＋ｚ２＋
２ｘｙ＋２ｙｚ＋２ｚｘ です。
この展開式の項の係数の合計を数えればいいのではないかと思うわけです。
同様にして、Ｐ(３)を考えてみます。
(ｘ＋ｙ＋ｚ)３＝ｘ３＋ｙ３＋ｚ３＋３ｘ２ｙ＋
３ｘ２ｚ＋３ｙ２ｚ＋３ｙ２ｘ
＋３ｚ２ｘ＋３ｚ２ｙ＋６ｘｙｚ
項数を数えるなら、展開などしなくても３３＝２７でいいわけですが、この中で不的確な項を除かなくてはなりません。
つまりｘに相当するのが、一万円のお年玉とするならばこれは３つしかないので、ｘの次数の上限は３。
同様にｙ、ｚに相当するのが、五千円、二千円のお年玉とするならば、これらの次数の上限は２とします。
この条件にある項だけ拾いだします。
そうすると、ｙ３、ｚ３が条件に合いませんのでこれを除外し、Ｐ(３)＝２５となります。
同様に次はＰ(４)です。
(ｘ＋ｙ＋ｚ)４＝４ｘ３ｙ＋４ｘ３ｚ＋６ｘ２ｙ２
＋ｙ２ｚ２＋６ｚ２ｘ２
＋１２ｘ２ｙｚ＋１２ｙ２ｘｚ＋１２ｚ２ｘｙ＋・・・
条件に合う項の係数の合計だけ数えます。
Ｐ(４)＝４・２＋６・３＋１２・３＝６２
Ｐ(５)です。
(ｘ＋ｙ＋ｚ)５＝１０ｘ３ｙ２＋１０ｘ３ｚ２＋２０ｘ３ｙｚ
＋３０ｘ２ｙ２ｚ＋３０ｙ２ｚ２ｘ＋３０ｚ２ｘ２ｙ＋・・・
条件に合う項の係数の合計だけ数えると、
Ｐ(５)＝１０・２＋２０＋３０・３＝１３０
Ｐ(６)です。
(ｘ＋ｙ＋ｚ)６＝６０ｘ３ｙ２ｚ＋６０ｘ３ｙｚ２＋９０ｘ２ｙ２ｚ２
＋・・・
条件に合う項の係数の合計だけ数えると、
Ｐ(６)＝６０・２＋９０＝２１０
Ｐ(７)です。
(ｘ＋ｙ＋ｚ)７＝２１０ｘ３ｙ２ｚ２
＋・・・
条件に合う項は１つだけで、
Ｐ(７)＝２１０
| NO.917 | 2001.1.9. | かつ | 箱の問題・その後（４） |
作図の問題で思い出したのですが、正17角形を作図できますか？
| NO.918 | 2001.1.9. | Junko | お年玉（３） |
NO.916で、(ｘ＋ｙ＋ｚ)６や(ｘ＋ｙ＋ｚ)７の展開を
あっさり書きましたが、これは自分で計算したものではありません。
「Mathematica」というソフトを使って、展開しました。
手計算でやるにはどうしたらいいか？
すべての展開をする必要はないわけで、必要な項の係数だけわかればいいわけです。
展開公式
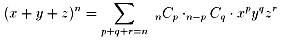
(ｘ＋ｙ＋ｚ)７の展開式におけるｘ３ｙ２ｚ２の係数を知りたい場合は、
ｎ＝７、ｐ＝３、ｑ＝２とすれば係数は、７Ｃ３・４Ｃ２＝２１０
という計算で得ることができます。
| NO.919 | 2001.1.9. | 浜田 明巳 | インドの数学事情 |
ＡＥＲＡ’０１．１．０８
雑誌ＡＥＲＡの上記号にインドの数学事情についての記事がありました。
考えさせる内容でした。タイトルは「数学が人生を決める国（インドＩＴ躍進の背景に英才教育）」。
インドの数学カリキュラムでは、日本と比べてすでに６年（小６）で
負の数、二乗、文字式、１次方程式、統計
７年（中１）で
指数、因数分解、三平方の定理、三角形の合同条件
８年（中２）で
平方根、三乗根、複利、株式、球の表面積と体積
９年（中３）で
集合、対数、三角関数、コンピュータのフローチャート
等を学習するようになっています。日本と比べて１年も２年も早い内容です。
１０年生と１２年生の終了時には進級・卒業試験が課せられ、
そこで各科目４割程度以上の成績を収めなくては進級、卒業が出来ない。
その卒業試験問題も日本の中堅工科系大学の入試レベルだそうです。
大学入試では、線形代数や微分方程式等の大学１、２年レベルの問題もあり、
大学院の入試にしてもおかしくないものもあるとか。
「インドで数学が重視されているのは、かつてゼロを発見したという国民的自負や
優秀な数学者が輩出しているという伝統もあるが、国力を高めるには高いレベルの技術者が必要であり、
数学があらゆる技術の基礎だという共通認識があるからだ。
高度な教育が行われ、激しい競争があるからこそ国際レベルで通用する技術者が育っていく。
カリキュラムをやさしくするなんて誰も考えない。」との話もありました。
ただし小学校の授業風景を見てみると、先生がいきなり複雑な計算式を黒板に書き、
早口で説明しながら、どんどん答を書いていく。順序だてて説明せず一気に高度な内容に入って
いくのです。「まとめて一度に教えた方がかえって理解しやすい。」という先生の言葉でしたが、
ついていけない子供達もいるようです。
「インドの教師たちの教え方はまだまだ洗練されているとはいえない。」とのことでした。
数学は貧困脱出の為の子供達の蜘蛛の糸なのです。
膨大な数の落ちこぼれを生みつつも詰め込み教育を強行し、
一人でも多くの数学エリートを育てようとするインド。
これは日本の、内容を削減し一人の落ちこぼれも出さない指導要領とはまったく
逆方向を向いています。しかし、文化的な違いもありどちらがいいとは言えないのでしょう。
インドでは「全員が理解でいる」カリキュラムなど絵空事に過ぎないというインド固有の
事情もあるのです。カースト制度による貧富の差が激しく、
上流階級はいくらでもお金をかけて教育を受けられるのに、
そうでない人達はほとんど授業にも出られない。
インドでは、コンピュータの教育がさかんで、世界中にインド人のコンピュータ技術者が
散らばっています。インドのスラム街に誰でもさわることが出来るコンピュータが
壁に埋め込まれていて、子供達は最初見よう見まねでさわっていたパソコンも、
あっという間に上達して、いろいろなことが出来るようになる。
インターネットでどんどん知識を吸収していくそうです。
スラム街ということを別にすると、実に羨ましい環境です。
古代インドの教えはコンピュータと親和性があり、実際サンスクリット語と
コンピュータのプログラム言語はよく似ているとのこと。
「コンピュータ工学はインド人の遺伝子の中に元々組み込まれている」
と結論づけていましたが、これは言い過ぎなのでしょうか？
世界に通用するエリートを育てる為に、英才教育を施し、
ついて行けない子供達を無視していいのか、教育内容削減の日本の現状がいいのか、
複雑な気がします。
| NO.920 | 2001.1.9. | 浜田 明巳 | インド工科大学入試問題 |
インド工科大学入試問題を紹介します。
E-mail
戻る