Weekend Mathematics／問題／問題44



４４．ハスの問題

睡蓮

湖に野生しているハスに関する問題です。
水面から１０インチつきでているハスの花がそよ風にゆれると、 ２１インチはなれた水面にふれる。
さて、水の深さはどのくらいですか？

はすの図
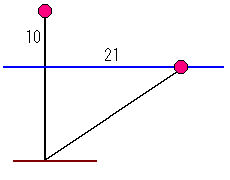
これはハスではなく、すいれんです。





問題の出典


サム・ロイドのパズル百科

マーチン・ガードナー編　田中勇訳

白揚社





答えと解説












答えと解説

解答・その１

（ペンネ−ム：RJCX）

お手上げです。花ってことは、花びらがつかえたって水面に触れるということでしょうか？
あの問題を自分ナリに解釈してやってみましたけど、さっぱりです。
水中部分を「X」インチと置きます。よって、１０インチ＋Xインチ・・・が長さです。
そこで、開き直ります。花の頂点が２１インチ離れた水面についたときを「ふれた」 としてしまえということです。
そう考えると、三角形が出来あがります。ここで、茎は水面と垂直に交わっていると します。
水中部分「X」、茎と垂直に交わっている点から２１インチ離れた所までの部分 「２１」、 そして、長さの「10＋X」の三つで三角形をつくります。
（←これの状態は、そよ風によって茎の付け根から倒された状態・・・いいのか（笑）！？）
　三平方の定理により、
X２＋２１２＝（10＋X）２
＝１００＋２０X＋X２
移項すると　　４４１＝２０X＋１００
２０X＝３４１　　　　　　X＝１７．０５　
という答えが出ました。というか、自分で問題作っちまったなぁ（核爆）



解答・その２

（ペンネ−ム：YUTAKA）

答えは341/20です。
計算過程は下記のとおりです。
まず、水深をxインチとすると、蓮の長さは(x＋10)インチで示されます。
そして、水面と蓮は垂直に交わっているので次のような式が成り立ちます。
(x+10)２=x２+21２となり、答えが算出できる。



解答・その３

（ペンネ−ム：GITANES）

水面下の蓮の長さをＸとおくと蓮の全長はX+10
三平方の定理により（X+10)２＝X２+21２
20X+100＝441となるのでX＝17.05



解答・その４

（ペンネ−ム：かぷち）

深さをＸインチとすると根の部分から花の部分までの長さは（Ｘ＋１０）インチと現される。
そよ風に揺れる前と水面と揺れて触れた水面とで囲まれた三角形に三平方の定理を用いて
Ｘ２＋21２=(X+10)２
これを解いて　　　X=17.05
答え 17.05インチ



解答・その５

（ペンネ−ム：ぱぶろ ）

はすの根は動かないものとし、 かつ、茎が途中で曲がらないものとすれば、花の動きは根を中心に半径Rの円を描くので

(A)　ハスの花が真ッすぐに立っているとき（水面に直交している）、 水の上に１０インチ花が出ている＝＞水の深さは　R-10インチ

(B)　風に流されて水面に花が着いた時＝＞２１インチ離れた位置で着水
　　根を中心に半径Rで描かれた円弧が水面と交差した。

(A),(B)から根を中心とした直角三角形が描ける
　　（A)から　垂線上の辺が　　　R - 10　インチ
　　（B)から　水平線上の辺が　２１　インチ　かつ、この時に斜辺がR。

これらの条件から　
　 　ハスの茎の長さが　R=２７．０５インチ、
　 　水の深さは　１７．０５インチ　として求まります。




解答・その６

（ペンネ−ム：マスター）

水の深さをｘとする。
(ｘ＋１０)2＝ｘ2＋212
２０ｘ＋１００＝４４１　　　　２０ｘ＝３４１　　ｘ＝１７．０５
　　　　　 答え１７．０５




解答・その７

（ペンネ−ム：Ryubi）

はすの図

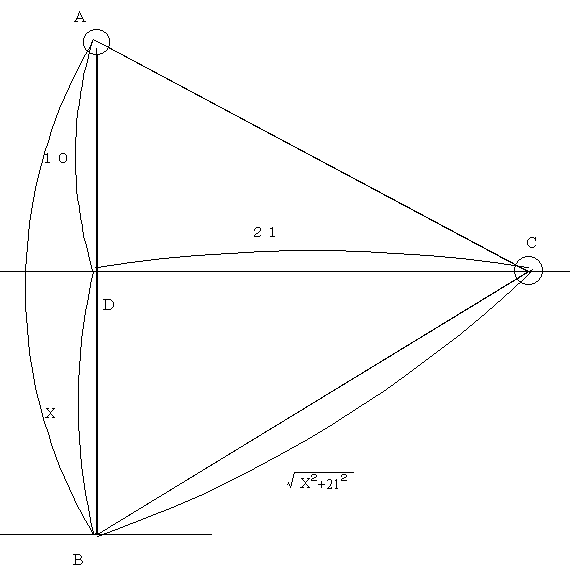
条件よりAB=CB,
三平方の定理より　CB２=X２+21２
(X+10)２=X２+21２
X２+20X+100=X２+441
∴X=341/20=17.05
Ans. 17.05インチ





解答・その８

（ペンネ−ム：もんさん ）

はすの図

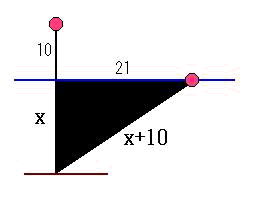
水の深さをＸインチとすると 図でできた三角形は直角三角形であるので 三平方の定理より
(Ｘ＋10)２＝Ｘ２＋21２
Ｘ２＋20Ｘ＋100＝Ｘ２＋441
20Ｘ＝441−100
Ｘ＝341/20　　　　　　　　答え　341/20インチ





解答・その９

（ペンネ−ム：少年Ｈ）

はすの図

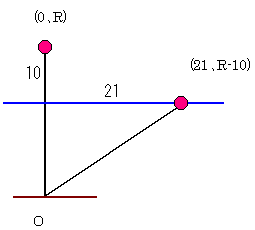
根元を原点、茎の長さをRｲﾝﾁとすると、元の花の位置は(0､R)、 水面に触れた時の花の位置は(21､R-10)となる。花の位置は、根元を中心として、 半径Rの円周上にあるから、水面に触れた時の位置は次の式を満たす。
２１２＋(Ｒ−１０)２＝Ｒ２ これを解くとR=27.05ｲﾝﾁ よって水深は 17.05ｲﾝﾁ




解答・その１０

（ペンネ−ム：yakabe）

はすの図

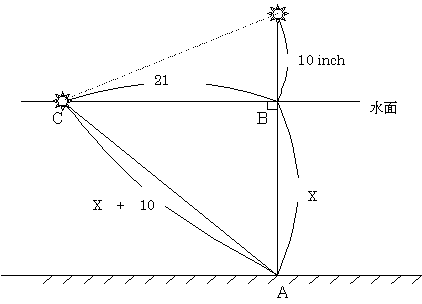
花の根元をA、花が風にゆれていないときの水面との交差点をB、 花が風にゆれて２１インチのところにふれた位置をＣ、求める水の深さをＸとする。
花の根元から風にゆれて水面にふれた位置までは直線的に考えて（１０＋Ｘ）インチである。 三角形ABCにおいてAB2 + BC2 = AC2 　であるから
X2 + 212 = ( 10 + X )2
X2 + 441 = X2 + 20X + 100
20X = 341
X = 17.05

A: 水の深さは最低でも17.05 インチはある




解答・その１１

（ペンネ−ム：浜田　明巳）

普通の解法は，他の人達が紹介して下さると思うので， いつもの用にＶＢのプログラムを組み，解きました．
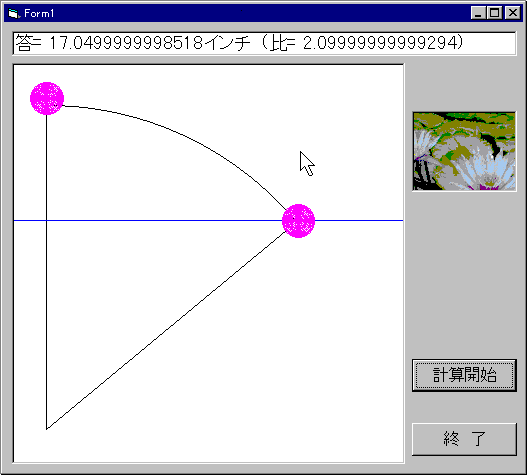
ハスを少しずつ倒していって，水面上の茎の長さと花が離れた距離の比が一番１０：２１に近くなる場合を求めています．
このプログラムにより，水の深さは１７.０５インチということが分かります．
　

VB form 

Option Explicit
Const pi = 3.14159265359
Const waku = 0.1
Sub Form_Load()
    Picture1.BackColor = vbWhite
    Picture1.Scale (-waku, 1 + waku)-(1 + waku, -waku)
    Picture2.BackColor = vbWhite
    Set Picture3.Picture = LoadPicture("suiren.bmp")
End Sub
Sub Command1_Click()
    Dim x As Double
    Dim y As Double
    Dim y1 As Double
    Dim y2 As Double
    Dim kizami(4) As Double
    Dim j As Integer
    Dim min As Double
    Dim x_min As Double
    Dim y_min As Double
    Dim sa As Double
    Dim ratio As Double
    Dim ratio_min As Double
    Dim kotae As Double
    For j = 0 To 4
      If j = 0 Then
        kizami(0) = 0.001
        y1 = 1 - kizami(0)
        y2 = kizami(0)
        min = 100
      Else
        kizami(j) = kizami(j - 1) * 0.01
        y1 = y_min + kizami(j - 1)
        If y1 > 1 - kizami(0) Then
          y1 = 1 - kizami(0)
        End If
        y2 = y_min - kizami(j - 1)
        If y2 < kizami(0) Then
          y2 = kizami(0)
        End If
      End If
      For y = y1 To y2 Step -kizami(j)
        x = Sqr(1 - y * y)
        ratio = x / (1 - y)
        sa = Abs(ratio - 21 / 10)
        If min > sa Then
          min = sa
          x_min = x
          y_min = y
          kotae = y * 10 / (1 - y)
          ratio_min = ratio
        End If
        Call sakuzu(x, y, y_min, kotae, ratio_min)
      Next y
    Next j
    Call sakuzu(x_min, y_min, y_min, kotae, ratio_min)
End Sub
Sub sakuzu(x As Double, y As Double, y_min As Double, kotae As Double, ratio As Double)
    Picture2.Cls
    Picture2.Print "答=" + Str(kotae) + "インチ  (比=" + Str(ratio) + ")"
    Picture1.Cls
    Picture1.Line (0, 1)-(0, 0), vbBlack
    Picture1.Line -(x, y), vbBlack
    Picture1.Line -(0, y), vbBlack
    Picture1.Circle (0, 0), 1, vbBlack, Atn(y / x), pi / 2
    Picture1.Line (-waku, y_min)-(1 + waku, y_min), vbBlue
    Call hasu(0, 1)
    Call hasu(x, y)
End Sub
Sub hasu(x As Double, y As Double)
    Dim j As Integer
    Dim kaisuu As Integer
    Dim hankei As Double
    kaisuu = 20
    hankei = 0.05
    For j = 1 To kaisuu
      Picture1.Circle (x, y), hankei / kaisuu * j, vbMagenta
    Next j
End Sub
Private Sub Command2_Click()
    End
End Sub




　

正解者

RJCXRyubiYUTAKA
数楽家ＣｒａｎｅyakabeGITANES
もんさんかぷち少年Ｈ
浜田　明巳ねこmhayashi
ぱぶろ中数の基本マスター
かつ水の流れ夜ふかしのつらいおじさん
マサボーやましたくん





まとめ

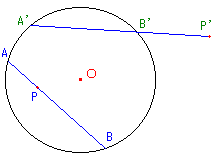方べきの定理
図１

寄せられた解答は(もちろん私も含めて)すべて三平方の定理を用いた解法でした。
水の深さをｘとおいて方程式をたてると、一見２次方程式に見えますが、実は１次方程式でして従って解が１つみつかります。
それならば、最初から１次式で解く解法はないものかということで、別解を紹介します。
その準備として「方べきの定理」を紹介します。

方べきの定理(図１)

定円Ｏと定点Ｐについて、ＰＡ・ＰＢ＝一定

方べきの定理
図２

方べきの定理の簡単な証明をします。(図２：点Ｐが線分ＡＢ上にあるとき)
ＰＡ・ＰＢ＝(ＡＭ−ＰＭ)・(ＡＭ＋ＰＭ)
＝ＡＭ２−ＰＭ２
＝(ＯＡ２−ＯＭ２)−(ＯＰ２−ＯＭ２)
＝ＯＡ２−ＯＰ２
＝一定

点Ｐが線分ＡＢ上にない場合も同様に証明ができます。

方べきの定理
図３

方べきの定理を別な形で表現します。(図３)
１つの円に弦ＡＢ，ＣＤがあり、その交点をＰとすると、以下の等式が成り立つ。
ＰＡ・ＰＢ＝ＰＣ・ＰＤ

方べきの定理
図４

さてハスの問題に戻ります。(図４)
方べきの定理により、
ＢＥ・ＢＦ＝ＢＡ・ＢＤ
つまり　21×21＝10×ＢＤ
従って、ＢＤ＝44.1
つまりこの円の直径ＡＤ＝44.1+10＝54.1
そして半径ＡＣ＝54.1/2＝27.05
答え　ＢＣ＝ＡＣ−ＡＢ＝27.05-10＝17.05








E-mail 戻る top