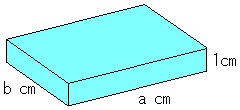
タテaセンチ、ヨコbセンチ、厚さが1センチの箱があります。
タテとヨコの長さをかけ合わせたabセンチの長さを作ってください。
Weekend Mathematics/問題/問題48
48.箱の問題

タテaセンチ、ヨコbセンチ、厚さが1センチの箱があります。
タテとヨコの長さをかけ合わせたabセンチの長さを作ってください。
別冊サイエンス ひらめき思考 Part2
I.C.フリッカー編
日経サイエンス社
答えと解説
(ペンネ−ム:SHO)
1cm×1cm×xcmの十分に長い筒を用意します。
次に箱を満タンの水の中に沈めてあふれた水をろうとかなにかでさっきの筒の中に入れます。
abミリリットルのがはいるはずなので、
水平な地面に置けばabセンチメートルになってるはずです。

(ペンネ−ム:久史)
こんなのはどうでしょうか?
まず箱いっぱいに水をいれます。それから縦1cm横1cmの箱を作って
その箱に水を移せば体積がabだから当然高さもabになります。よね?
でもこれってめんどくさすぎかな?
水も用意しなきゃいけないし新しく箱まで作らなきゃいけないし・・・
まいっか作ってくださいっていってるしね。

(ペンネ−ム:柿本 浩)
・箱は1つだけではなく任意の個数用意できる
・箱はいくつ積み重ねても自らの重みで変形したり、潰れたりする事はない
・作業は無限に広がる水平面上で行うものとする
以上の事を仮定した上で解答させて頂きます。
○パターン1:a、bが共に自然数であった場合
・a×bの面積を持つ面を底面とし、同じ形で
縦にa×b個積み上げることで、高さがabとなる
・a×1の面を底面とし、同じ形で
縦にa個積み上げることで、高さがabとなる
・b×1の面を底面とし、同じ形で
縦にb個積み上げることで、高さがabとなる
○パターン2:a、bのどちらか一方が自然数、他方が純少数または帯小数であ
りa×b=自然数であった場合
・a×bの面積を持つ面を底面とし、同じ形で縦にa×b個積み上げることで、
高さがabとなる
・aが自然数ならばa×1の面(bが自然数ならばb×1の面)を
底面とし、同じ形で縦にa個(b個)積み上げることで、高さがabとなる
○パターン3:a、bのどちらか一方が自然数、他方が純少数または帯小数であ
りa×b≠自然数 であった場合
・aが自然数ならばa×1の面(bが自然数ならばb×1の面)を
底面とし、同じ形で縦にa個(b個)積み上げることで、高さがabとなる
○パターン4:a、bが共に純少数または帯小数であった場合
・複数積み重ねることでの実現は不可能
○全パターン共通
・a×1(またはb×1、a×b)の面を底面として箱を置き、空間に点光源を配
置する
この時、点光源の位置は
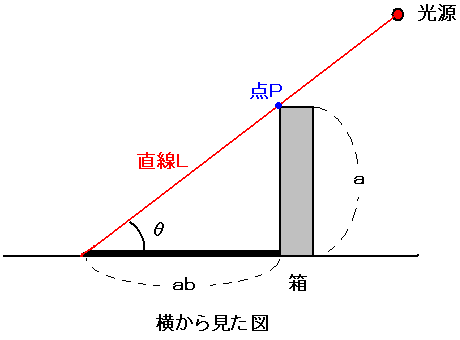
まず、高さaとなるように箱を置いて(この時b×1の面が底面になりますよね)
影の長さがabとなるような角θを考えると、
tanθ=高さ/底辺なので当然tanθ=a/ab=1/bとなりますよね?
つまりb×1の面を底にした場合、tanθ=1/bとなる角度で光を当てれば影の長さはabになる、と。
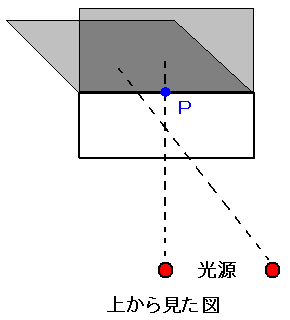
ただし、一定の長さの影を作るためには、光線が箱の面に対して垂直に差し込む必要があるので
「上面のいずれか1辺の垂直二等分線を回転させてできる平面」という表現を用いた訳です。
実際にきれいな方形の影を作るためには、1点だけではなく、箱の表面全体に対して光線が垂直に
差し込む必要があるので細かく言えば点光源ではダメなのですが、そこまで言い出すとキリが無いのでお見逃し下さい(笑)
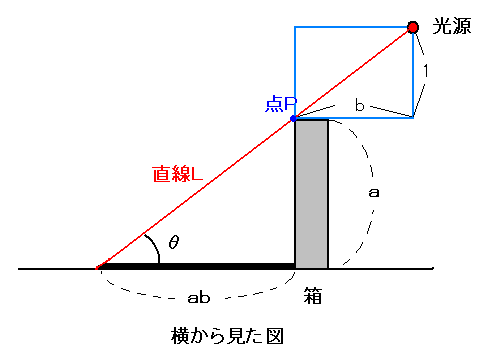
コメント(Junko)
2つ目の図は、光源をどこにおくかという説明かと思いますが、要は断面が「横からみた図」のよ
うになればいいわけですよね? ・・・と私は理解しました。
光源から光りを当てるやり方はわかりましたが、問題はtanθ=1/bとなる角度
をどう作るかということではないかと思います。
思うに「横から見た図」の箱の上に点Pが重なるような形で横b、縦が1となるように同等の箱
(同じ箱が2つあるという保証はあるのか? といわれると困るけど・・・・)をお
けばいいのではないかと思います。
・重力加速度を9.8m/s2、空気抵抗は考えないものとすると
充分な高さから箱を自由落下させた時の落下距離は、落下時間をt秒として
(1/2)×9.8×t2[m] となる
ab[cm]=ab/100[m] であり
(1/2)×9.8×t2=ab/100 となる時間tは
t=(ab/490)1/2となる
つまり、充分な高さから箱を自由落下させて
(ab/490)1/2秒経過した時の落下距離がabセンチとなる
正解など存在しないこうした「発想の問題」は大好きなのですが
私の発想力ではとりあえずこんなところです(^^ゞ
「箱を切断して・・・」というのも考えてみたのですが
それだと何でもアリアリになってしまうのでさすがにやめました。
ま、おそらく一番多い解答は
・引出しを開けてドラえもんを呼び出し
ビッグライト(or スモールライト)で
箱をa倍(b倍)の大きさにしてもらう
なんでしょうけどね(笑)

(ペンネ−ム:Oitan)
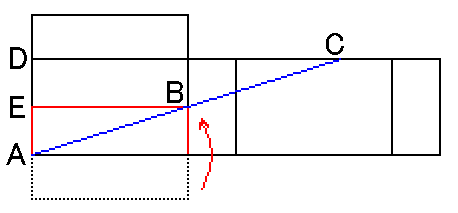
Take one "a times b" rectangular of the box and name each corner as A, B, C, and D, where AB=CD=a and BC=DA=b. Take point E on the extended line of DA, where EA=1 (we can get a length of 1). Draw a line which passes through E and B. Also draw a line which is the extention of DC. Intersection of both two lines will be called as F. Now we have two right trianlges of FCB and FDE, where angle FCB and FDE are 90 degree, and both are similar. Here FC is equivalant to ab. Let's prove this. Let FC=x. Now we have FC : FD = BC : ED, ie, FC : (FC+CD) = BC : (AD+AE). Then we get x : x+a = b : b+1. So we get x=FC=ab. It is very tough to explain verbaly (in English) without any illustration, but hope this makes sense for you and is OK.
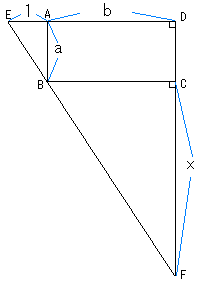
図をつけて、日本語に訳してみます。(Junko)
a×bの長方形の箱の各頂点をA、B、C、Dと名付ける。
このとき、AB=CD=a、BC=DA=bとする。
辺DAの延長上に、EA=1となるように点Eをとります。
(長さ1は箱の高さより、得ることができます。)
点Eと点Bを通る直線をひきます。
更に、辺DCも延長します。
この2本の直線の交点を点Fとします。
直角三角形△FCBと△FDEを考えます。
これらは、∠FCB、∠FDEがそれぞれ90゜で、互いに相似の関係です。
ここで、FCはabに等しいことがわかります。
これを証明しましょう。
FC=xとすると、
FC:FD=BC:ED、すなわちFC:(FC+CD)=BC:(AD+AE)
x:x+a=b:b+1
従って、x=FC=ab
イラストをつけずに英語で説明するのは、とてもむずかしいことです。
理解してもらえれば幸いです。

(ペンネ−ム:高橋 道広 )
abを作れという問題ですが、いかにもあやしい。
定規を使えとか何も書いていないのはなぜでしょう。
そこで回答は、粘土をこのはこの中にいれて、その粘土の断面積が1cm2に
なるように、整形する。すると長さがabになる。
ということでどうでしょう。
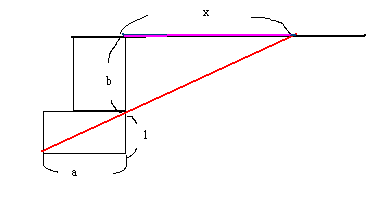
別解 1
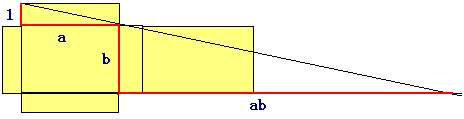
別な回答としては、添付の図のように、黒い直方体を組み合わせることにより、
赤い線を引くと a:1=x:b x=abとピンクがabとなります。
図のなかの線は直方体を何個か置くことによってできます。
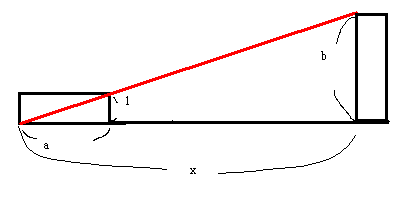
別解 2
図のように左に1つおいて、3つの頂点が一直線上になるように、右の直方体を調整します。
するとx=abです。
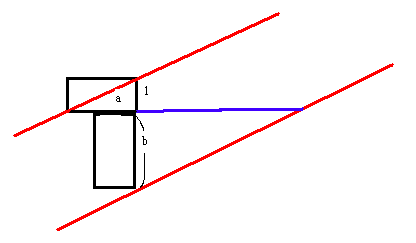
別解 3
まず赤い平行線をひきます。これに、2つを組み合わせた黒い直方体を図のように
頂点が線上にくるように置きます。すると青い線がabになります。

(ペンネ−ム:夜ふかしのつらいおじさん )
先ず、箱をていねいに切り開きます。(図の黒) なぜなら、△ABEと△ACDが相似なので、 (ペンネ−ム:ねこ) 1:b=a:abより、
図のように作図できる。
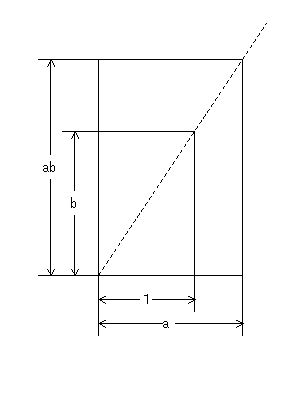
(ペンネ−ム:中数の基本) 1という長さをどのように生かすかがポイントです 左の図のように,展開図にし,対角線を延長すると,相似図形の比例関係からabという
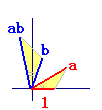
長さが得られます. なお,同種の問題として,高校の複素数平面で,「1及び複素数a,bが図のように与えら
れているとき,複素数abを図示せよ」という問題においても,1という長さを生かすこと
がポイントとなります.
問題の問いかけ方が曖昧だったために混乱を招いたかもしれません、ごめんなさい。
数学流に解釈するならば、これは「定木とコンパスを用いて作図しなさい。」ということになると思います。 さて、「定木とコンパスを用いた作図」について、少しお話しましょう。
(参考:数学100の問題/日本評論社)
さて、高橋 道広さんからの発展問題です。 (1)今回の問題で (2)定規とコンパスでできるものは、コンパスだけでできるという定理があるそうです。 (3)3等分点はどうでしょう (1)は、方程式x2=abを解けばいいわけですから、可能ですね。 関連した内容がコロキウム室 NO.912にあります。
次に、図のように縦の部分を折り返します。(赤)
AE:EB=AD:DC
AE=1、EB=a、AD=bなのですから
DC=abとなります。

解答・その7

解答・その8

正解者
Oitan SHO 高橋 道広
夜ふかしのつらいおじさん 中数の基本 柿本 浩
ねこ 久史

まとめ
でも、もっと広い解釈をしてもいいのではないかと思います。
いろいろな発想で、アプローチしていただいていいと思います。
SHOさんや、久史さん、
高橋 道広さんの粘土の解答のような解答は現実的でおもしろいと思います。
(それぞれ必要な道具をそろえることを考えると、逆に非現実的かもしれない?)
面積を長さにというように次元を下げる場合、パラメーターの1つを単位数1にすると
いうのは当然発想としてはあると思いますから、私は正解でいいと思います。
柿本 浩さんもとてもユニークな解答を寄せていただきました。
1番最後の解答は、地球の重力加速度を使うわけですね。
そもそも長さの単位などの基準を決める時には、自然界にあり、ほぼ普遍と思われるも
のを使ったりするわけですから、そういう意味では自然かもしれません。
ただ問題は、(ab/490)1/2秒を測るということに置き換えただけですから問題の解決にはなっていないのかな?
定木は直線を引く道具、コンパスは円(定点から距離の等しい点の集合)を描くものです。
この2つの道具を使って求めることのできる点は、直線と直線の交点、直線と円の交点、円と円の交点です。
これらはいずれも2次方程式(含む1次方程式)の解を求めることに他なりません。
従って、2次方程式(含む1次方程式)に帰着できる作図問題は解けることになります。
逆に、2次方程式(含む1次方程式)に帰着できない作図問題は解けないということです。
幾何学の3大問題といわれるものの1つに「任意に与えられた角を3等分すること(角の3等分問題)」
というものがあります。
1837年にワンツェルという人が、「作図不可能である」ということを証明しました。
つまり、この作図問題を方程式におきかえた時、それが3次方程式になるからです。
3大問題の残る2つは、「与えられた立方体の体積の2倍に等しい体積をもつ立方体を作図すること(立方体倍積問題)」と
「与えられた円と同じ面積を持つ正方形を作図すること(円積問題)」です。
前者は、方程式x3=2a3を解かねばなりませんから不可能です。これもワンツェルが証明しました。
後者は、リンデマンが1882年にやはり不可能であることを示しています。
方程式x2=πa2を解けばいいわけですが、
ここでπが超越数であることから、不可能であることを示したわけです。
超越数とは、代数的方程式の解にならない数です。
幾何学の3大問題はいずれも「不可能の証明」をもって決着したわけです。
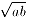 を作ってください。
を作ってください。
では、2点A,Bの中点をコンパスだけで求めてください。
ただ、どうすればそれが具体的に求まるかというのは別問題です。
(2)本当? 詳しくご存知の方がいたら教えてください。
(3)は、方程式x=(1/3)aを解けばいいということですね。
さて作図はいかに?
皆さん、よろしくお願いします。

 E-mail
E-mail
 戻る
戻る
 top
top