Weekend Mathematics/コロキウム室/2000.10〜12/NO.101
コロキウム室
| NO.861
| 2000.10.1. | Junko | リーグの勝ち点(2)
|
問題1:
A、B、Cの3チームがリーグ戦をすると、組み合わせは3C2=3通り。
それぞれの試合について、一方が勝つ場合、負ける場合、引き分けの場合と3通りの勝敗が考えられるので、
33=27通りのケースが考えられます。
それらをすべて挙げてみました。
得点の取り方のパターンは7通り。
- 6−3−0 ・・・6通り(2勝するチームが3通り×1勝するチームが2通り)
- 6−1−1 ・・・3通り(2勝するチームが3通り)
- 4−3−1 ・・・6通り(1勝1引き分けのチームが3通り×1勝のチームが2通り)
- 4−2−1 ・・・6通り(1勝1引き分けのチームが3通り×2引き分けのチームが2通り)
- 4−4−0 ・・・3通り(1勝1引き分けが2チームで3通り)
- 3−3−3 ・・・2通り(じゃんけん状態、右回りと左回り)
- 2−2−2 ・・・1通り(すべて引き分け)
以上、合計で27通り。

| NO.862
| 2000.10.1. | 月の光 | ビュッフォンの針の実験(4)
|
NO.441のビュフォンの針の問題では間隔がdの平行線をたくさん引き、
長さkの針をばらばらに落としたとき、 針が平行線と交わる確率pを
求めますが、ではy=sinθ,y=sinθ+d,y=sinθ+2d,y=sinθ+3d・・・
と無限に線を引き、その上に長さkの針を落としたときに線と針が交わ
る確率はどうなるでしょうか。

| NO.863
| 2000.10.2. | Kernighan | 三角数の数列(4)
|
NO.859 三角数の数列(3)では、
力づくの証明だったので、別証を考えました。
T(k)=k(k+1)/2, k=0,1,2,...とすると
n=2m ⇔∀k∈{0,1,...,n-1}に対し∃l;T(l)≡k(mod n)
まず T(k+l)-T(k-(l+1))=2kl+k (1)を示す。
実際、T(k)=k+T(k-1)を繰り返し使うと、
| T(k+l)
|
| = | (k+l)+T(k+l-1)
|
| = | (k+l)+...+(k+1)+k+(k-1)+...+(k-l)+T(k-(l+1))
|
| = | kl+(1+...+l)+k+kl-(1+...+l)+T(k-(l+1))
|
| = | 2kl+k+T(k-(l+1))
|
→
n個の{T(k)} k=0,1,...,n-1が全て異なる(mod n で)ことを示せばよい。
帰納法でしめす。
m=1のときは明らか。
n=2m のとき成り立つと仮定する。
(1)で k=2mとおくと
T(2m+l)-T(2m-(l+1))=2m+1l+2m (2)
より、T(2m+l)≠T(2m-(l+1)) (mod 2m+1)
また、仮定から{T(2m-(l+1))}は mod 2m で全て異なるので
mod 2m+1で全て異なる。
さらに、{T(2m+l)}も mod 2mで全て異なる。
実際、(2)より、
T(2m+l)≡T(2m-(l+1)) (mod 2m)
で、仮定から{T(2m-(l+1))}は mod 2mで全て異なるので、
{T(2m+l)}も mod 2m で、すなわち mod 2m+1で全て異なる。
以上より、n=2m+1のとき、{T(k)}は mod 2m+1で全て異なる。
←
次が成り立つことに注意する。
∀k≧nに対し∃l∈{0,1,...,n-1};T(k)≡T(l) (mod n)
実際、k=an+l=(a+1)n-(l'+1) とかけて、
anが奇数ならば
T(k)-T(l)=(k+l+1)(k-l)/2=(2l+an+1)an/2 で
(2l+an+1)は偶数なので T(k)≡T(l) (mod n)
anが偶数ならば (a+1)n は奇数で
T(k)-T(l')=(a+1)n((a+1)n-(2l'+1))/2 で
((a+1)n-(2l'+1))は偶数なので T(k)≡T(l') (mod n)
対偶をとって上の注意から、
n≠2mのとき、∃k,l 0≦l<k<n; T(k)≡T(l) (mod n)を示せば十分であ
るが、
n≠2m⇔n が奇数を含む⇔n=(2l+1)kとかける。
従って、T(k+l)≡T(k-(l+1)) (mod n)

| NO.864
| 2000.10.11. | 山人 | 確率分布(6)
|
NO.839の確率の問題は大変興味深く読ませていただきました。
最後の結果について,エクセルで乱数を発生させてシュミレーションしました。
nは100として、1000回分のデータをとってみました。
結果は(n−3)/6とよくあいます。

| NO.865
| 2000.10.12. | 水の流れ | 24と互いに素
|
太郎さんは、今日授業で、24以下で24と互いに素な数を黒板に書いていました。
すなわち、1,5,7,11、13、17、19、23 の8個です。
そこで、一般に、2の倍数でも3の倍数でもない自然数の数列を作ります。
ここで、問題です。
問題1:この数列の一般項をnで表せ。
問題2:この数列の初項から2m項までの和をmで表せ。

| NO.866
| 2000.10.12. | 水の流れ | 新左衛門の望み(1)
|
「今日は米1粒をください。そして、明日からは前日の2倍のづつ1ヶ月の間ください。
1粒、2粒と日々戴くのは面倒ですから1ヶ月後にまとめて戴きたい」
皆さん!こんな話を聞いたことがあるでしょう。戦国武将豊臣秀吉(1537〜1598)の御伽衆
(お話相手をする人々)の1人に泉州堺の鞘師(刀の鞘を作る職人)の曽呂利新左衛門(?〜1603)
がいました。彼は鞘師としての腕前だけでなくおどけた話や狂歌の名手として、機知に富み話上手で、
常に秀吉のそばに仕え大変恩寵を受けていました。
あるとき、秀吉が新左衛門に何か褒美を与えるが何が欲しいかを尋ねると、
新左衛門は、「今日は米1粒・・・。」と望み、秀吉も「何だその位の望みか」と簡単に承知しました。
そこで、皆さん!米50粒で1グラムとして計算します。ただし、1ヶ月30日とします。
問題1:一体何トン位になるか計算してください。
問題2:米60kgで1俵といいます。新左衛門は一体何俵の米俵をもらうことになるでしょう。
問題3:1年間に1成人はだいたい米を1俵位食べるといいます。
この米粒は1成人の年分にあたるでしょうか。
<参考文献:理系への数学11月号>

| NO.867
| 2000.10.13. | 浜田 明巳 | 新左衛門の望み(2)
|
粒数は,
1+2+22+23+・・・+229=(230−1)/(2−1)
=230−1
したがって,
(230−1)/(50×1000×1000)トンとなり,
(230−1)/(50×1000×60)俵となります.
UBASICで計算させると,だいたい
21.5トン
358俵
358年分
となります.

| NO.868
| 2000.10.13. | 水の流れ | 新左衛門の望み(3)
|
「浜田」さんの解答を見ていて、以外に多いなーとふと思っています。
そこで、ちょっと変かなと思い再度計算してみましたが、確かでした。
でも、納得が今一いかないので、考えてみると、
この戦国の時代の暦は一体何だったにたどり着きました。
私が、1ヶ月の日数がないと計算出来ないから、注釈をつけたのです。
そうです。この時期は今使っている太陽暦(グレゴリオ暦)ではなかったのです。
この暦は日本では明治五年に採用しています。
したがって、それ以前は月のみちかけを基準にした太陰暦が使われていたことに
気がついたのです。
旧暦では、29日の小の月と30日の大の月を交互に置くことにしていました。
平均の一月の長さは29.5日になります。
しかし、1年では約11日ずれてしまうので、この端数は3年で約1ヶ月になるので、
これを調節するために閏月という余分な月を入れて、1年13ヶ月の閏年を作っていました。
閏年の日数は平年に比べると30日ほど多くなっています。

| NO.869
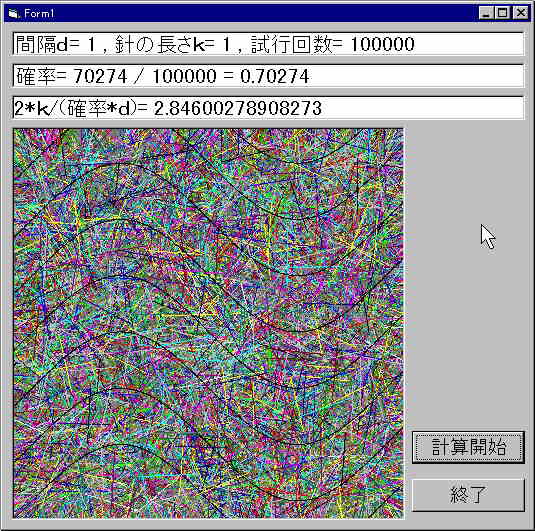
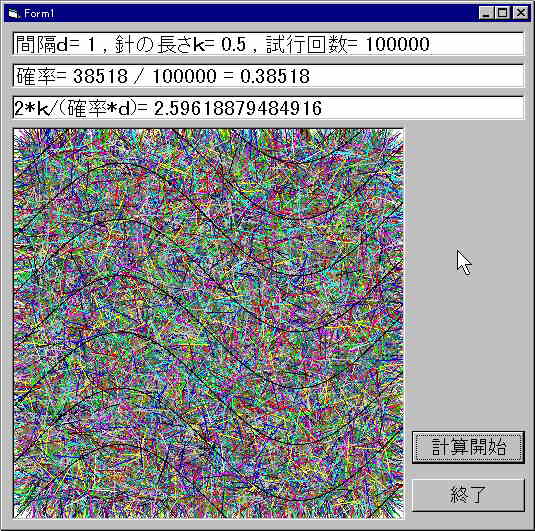
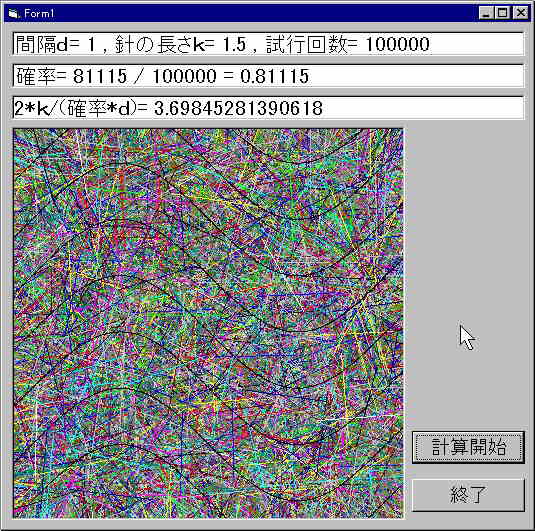
| 2000.10.14. | 浜田 明巳 | ビュッフォンの針の実験(5)
|
VBで実験したところ、以上のような結果になりました。精度が悪いせいか、いい結果とはいえないでしょう。

 E-mail
E-mail
 戻る
戻る













 E-mail
E-mail
 戻る
戻る