
Weekend Mathematics/コロキウム室/2000.7〜9/NO.97
| NO.831 | 2000.7.2. | 水の流れ | ゲーム料金 |
太郎さんは、先日夏祭りの夜店に行って来ました。
夜店の主人が、1,2,3,・・・、10の数字が書いてあるカードを持っていました。
それら10枚のカードを左右に1列に並べて、kという数字のカードが左からk番目にあれば、
kというカードにk×10円の引換券を与えてゲームをやっていました。
もちろん、無操作に並べて、インチキのないカードとします。
さらに、kという数字のカードがk番目にないなら、引換券はもら
えません。そこで、問題です
問題1:
このゲームをしたとき、一番高い並べ方をしたとき引換券はいくらになるでしょうか。
問題2:
10枚のカードについての引換券の期待値を求めてください。
問題3:
1夜にして、だいだい200人がこのゲームをしていくと仮定して、
9000円以上の利益を期待するにはゲームの料金をだいたいいくらにしたらよいでしょうか。
1円以下は繰り上げてください。
問題4:
また、カードの数字が1から、nまで書いてあったときの、引換券の期待値をnで表してください。

| NO.832 | 2000.7.3. | Junko | 「放浪の天才数学者エルデシュ」 |
私もNO.810の「水の流れ」さん同様、5月21日朝日新聞の記事
にある「放浪の天才数学者エルデシュ」(草思社)を読みました。
1996年9月20日、ポ−ル・エルデシュは心臓発作で亡くなった。享年83才。
ポ−ランドのワルシャワで開催された組み合わせ論のセミナ−に出席中、問題を解き終えて次の問題に 移ろうとしたときに倒れ、病院へ運ばれたが、その午後に息をひきとった。まさにかれが生前希望していた通りの逝き方だった。
エルデシュは数学界ではきわめて有名な「伝説的」人物だったそうだ。 早熟な天才であったし、奇矯な振る舞いも語りぐさだったという。 ところが、専門外の人がアインシュタインのように広くかれを知ることはほとんどなかった。 おそらく、かれの興味がもっぱら数学を解くことと、数学をいっしょに解いてくれる同志をみつけだすことだけに向けられていたためだろう。
かれは、485人もの共著者と1000本以上の論文を発表し、 70歳を越えてからもなお1週間に1本は論文を書いたといわれる。 この共著者の多さからエルデシュ番号なるものが派生したり、相手構わず子どもをエプシロン、 女性をボス、男性を奴隷などと呼ぶ独特の単語や言い回しで話をしたり、 若い数学者を育成するために問題に賞金をつけて出題したり、濃いコ−ヒ−やベンゼドリンやカフェインの 錠剤を飲みながら1日に19時間も問題を解くという生活を送ったりと、「伝説」となる逸話には事欠かない。
定住地も家庭も財産も持たず、身の回りの品を詰めただけのス−ツケ−スを携えて25カ国以上を 飛びまわり、いきなり戸口に「わしの頭は営業中だ」と言って現れたというエルデシュ。 かれに宿を提供し、いささかのあきれとあきらめと、それ以上の敬愛をこめてかれと 語り明かした数学者仲間たちには、そして本書を読んでかれを知った読者には、単なる逸話以上のものが伝わっているはずだ。
「放浪の天才数学者エルデシュ」訳者(平石律子)あとがきより引用

| NO.833 | 2000.7.6. | Idaho Potato | エルデシュ数 |
No. 832のポール・エルデシュの話に出てきた「エルデシュ数」について、少々与太話をば…
「エルデシュ数」とは、次の法則によって数学者に付与される自然数(または∞)です。
エルデシュは共著者があまりにも多いので、上のようにエルデシュ数を定義すると、今日の著名な数学者の大部分は有限のエルデシュ数をもつことになります。
このことが、エルデシュ数なるものが派生したゆえんです。
また、エルデシュの偉大さゆえ、数学者の間では、比較的小さなエルデシュ数をもつことはある種のステータスと考えられています。
(エルデシュ数プロジェクトのWebサイトでは、エルデシュ数2以下の数学者のリストや、著名な数学者のエルデシュ数が公開されています。)
ちなみに、これを書いている私自身も、実はエルデシュ数有限です。
エルデシュから私に至る共著関係の連鎖をたどってみると、私とはまるで比較にならない大物数学者たちを経由しながら、ひょんなところで私に到達しています(^^;)。
さて、上述のエルデシュ数の定義を一般化することによって、数学者全体の集合(空間)に「距離」を導入することができます。
数学者全体の集合を M とし、 M のべき集合の部分集合 P を、「 { a0, ..., ak-1 } ∈ P となるのは、数学者 a0, ..., ak-1 らによる共著論文が存在するときかつそのときのみ」と定義する。
M の2つの元 a, b に対して自然数または記号「∞」を与える関数 e を、次のように定義する。
- M の任意の元 a について、 e(a,a) = 0 とする。
- M の相異なる2元 a, b に対して、 M の(n+1)個の元 c0, ..., cn および P のn個の元 p0, ..., pn-1 が存在して、 c0 = a、 cn = b かつ、 すべての i = 0, 1, ..., n-1 について、{ ci, ci+1 } ⊆ pi が成り立つとする。 このとき、そのような性質を満たす自然数 n のうち最小のものを e(a,b) の値とする。
- e(a,b) の値が以上によって定められない場合は、 e(a,b) = ∞ と定める。
e(エルデシュ,a) の値は数学者 a のエルデシュ数と一致するので、 上の定義は、エルデシュ数の自然な一般化になっています。 また、こうして定義された関数 e は、 いわゆる「距離の公理」、すなわち、次の3つの性質を満たします。 (ただし、記号∞については、任意の自然数 n について n < ∞、 ∞ + n = ∞ + ∞ = ∞ と約束します。)
したがって、数学者全体の集合 M に、この関数 e を距離関数として導入すると、 M は距離空間となります。
この距離空間で考えると、ひょっとしたら、意外な組み合わせの数学者同士が「ご近所さん」になっているかもしれません…
(参考文献: 「黄色いスミレの花の咲く頃」, 渕野 昌, 数学セミナー1997年7月号)

| NO.834 | 2000.7.17. | 水の流れ | n次元宇宙空間 |
太郎さんは、ときどき 夜空を見上げて、果てしなく続く宇宙空間を眺めています。
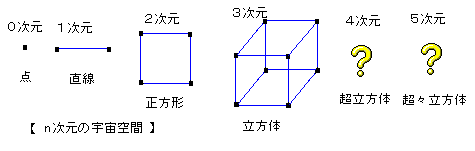
このとき、0次元の世界に住んでいると、そこには点の世界だから、
境界はひとつ「頂点」があるだけです。
この点を動かしてみると、1次元の世界ができあがるが、ここには「線」でしかない。
これには、「境い目」が2つある。
その両端である。言いかえれば、「2つの0次元境界(頂点)と1つの1次元境界(線)とがある」
と言える。
さて、この直線を横にその長さだけ引っ張ると、正方形ができる。
すると、頂点の数は、以前あった2から4に倍増している。
また、正方形では4つの直線、つまり辺が4本あり、さらに、
1枚の2次元境界(面)がここではじめて出てくる。
さて次ぎに、2次元の平面から上に向かって離れていくと、
例えば、正方形を上にうまく移動すれば、立方体を作ることができる。
4つの頂点の動いた軌跡がまず4本の線を作りだすから、辺は12本、頂点は8個、
面は2次元では、1枚しかなかったが、一挙6枚になっている。
これを、繰り返して、4次元の超立方体、5次元の超々立方体、・・・。
n次元の超々々・・・立方体を考えていきます。
ここには、n次元空間の世界があるのです。
このときの0次元境界(頂点)、1次元境界(辺)、2次元境界(面)、
3次元境界(立体)、・・・、(n―1)次元境界(名前はまだできていない)の数を調べたいのです。
ここには、オイラーの多面体定理が成り立つと思っていますが、・・・・
何せ、頭の中でしか想像できない超々々・・・立方体ですので、困っています。
ここで、問題です。
問題1:
4次元の「超立方体」には境界になる、点、辺、面、立体がそれぞれいくつあるでしょう。
問題2:
一般に、n次元の「超々々・・・立方体」には境界になる、点、辺、面、立体、・・・、
(n―1)次元境界の数は一体いくつあるでしょう。一般式が求められています。
皆さん考えてください。
<ヒント:群数列でみると、(1)、(1,2)、(1,4,4)、(1,6,12,8)、
・・・・>

| NO.835 | 2000.7.17. | 月の光 | DNAの問題 |
生物を特徴づける遺伝子DNAは次の4つの塩基からできています。
A=アデニン T=チミン
G=グアニン C=シトシン
この4つの塩基が対になって並んで蛋白質を作る元になっていますが、
たまに複製の際AがGやC、Tに換わって突然変異が起きてしまいます。
そこで問題です。
ある場所にAAAAAという配列があり、pの
確率でAがG(C、Tでもかまいません)に換わり、Gはqの確率で
Aに換わります。
n回目の複製でAAAAAとなっている確率を求めてください。
同様にm個のAが並んでいるときの確率を求めてください。

| NO.836 | 2000.7.27. | toshi | 確率分布(1) |
はじめまして。
今年の教員採用試験を受けたんですが、どうにもわからない問題がありました。
よろしければ、教えて下さい。
(問) 1からnまでの数字をかいたn枚のカード(n≧3)がある。
この中からまず、2枚を取り出し、次に、1枚取り出す(この数字をkとする)。
kが、最初に取り出した2枚のカードの間の数字なら確率変数Xを、X=k、
そうでなければ、X=−1とする。Xの確率分布を求めよ。
こんな感じだったと思うんですが・・・。
この後に、期待値を求める問題がありました。

| NO.837 | 2000.7.27. | Junko | 確率分布(2) |
まずXの確率分布を求めてみます。
P(X=1)=0・・・ありえないから
P(X=2)=(1/nC2)(1/n−2)=2/n(n−1)(n−2)・・・最初に取り出す2枚が1と3で、かつ3枚めが2
P(X=3)=(1/nC2)(1/n−2)=2/n(n−1)(n−2)・・・最初に取り出す2枚が2と4で、かつ3枚めが3
・・・以下同様
P(X=n−1)=(1/nC2)(1/n−2)=2/n(n−1)(n−2)・・・最初に取り出す2枚が(n−2)とnで、かつ3枚めが(n−1)
P(X=n)=0・・・ありえない
| P(X=−1) | =1−{P(X=1)+P(X=2)+・・・+P(X=n)}・・・上記のもの以外 |
| =1−(2/n(n−1)(n−2))×(n−2) | |
| =(n−2)(n+1)/n(n−1) |
次に期待値です。
| E(X) | =1×P(X=1)+2×P(X=2)+・・・+n×P(X=n)+(−1)×P(X=−1) |
| =1×0+{2+3+・・・(n−1)}×2/n(n−1)(n−2)+n×0+(−1)×(n−2)(n+1)/n(n−1) | |
| =(n+1)/n(n−1)−(n−2)(n+1)/n(n−1) | |
| =(n+1)(3−n)/n(n−1) |

| NO.838 | 2000.7.27. | toshi | 確率分布(3) |
例えば、X=3のときは、はじめの2枚が、2と5とかが、含まれていないように思えるのですが・・・。
P(X=3)=(1/nC2)(2C1)(n-3C1)(1/n−2)
一般的には
P(X=k)=(1/nC2)(k-1C1)(n-kC1)(1/n−2)
こんな感じになるのでしょうか?

| NO.839 | 2000.7.27. | Junko | 確率分布(4) |
そうですね、問題文はしっかり読まないといけませんね。
やり直します。
k=1〜nについては、NO.838のtoshiさんのご指摘通り、
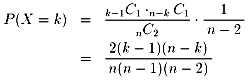
P(X=−1)については、
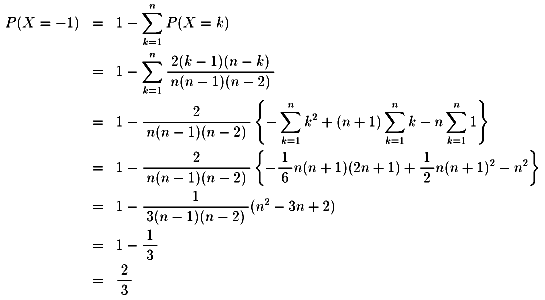
さらに期待値については、
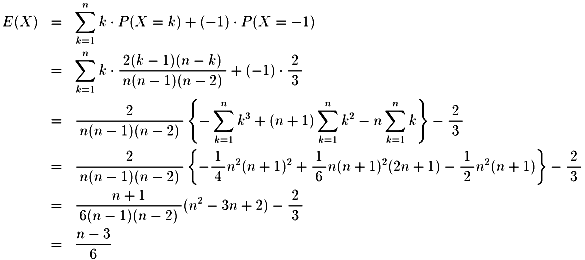
案外すっきりした形に落ち着きました。計算まちがいをしていなければ・・・。

 E-mail
E-mail
 戻る
戻る