Weekend Mathematics／コロキウム室／1999.4〜6／NO.52
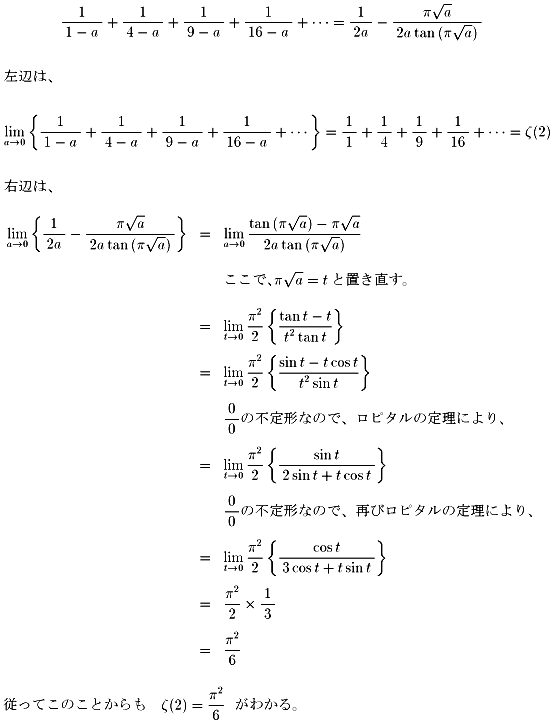
NO.436 '99 4/9 Junko オイラーの「無限解析入門（１）」（２）
NO.434で示された以下の式で、ａ→０としてみます。
NO.437 '99 4/9 Junko 折り曲げた台形の面積（５）
NO.432で「ヴァ−」さんがしたように、
JI=xとおけば、
GJ=x2、KF=x(2-x)となります。
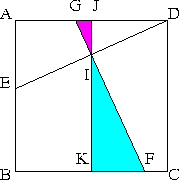
B=O(原点)、BCをx軸、BAをy軸とし、BA=BC=2とします。
そうすると、G(1-x2,2)、F(1+x(2-x),0)となります。
0≦x≦1としたときの、直線(正確に言うと線分)GFの奇跡を求めればいいことになります。
次に面積を求めます。
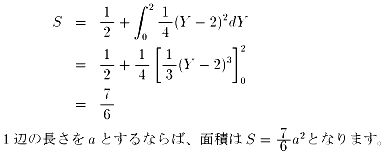
NO.438 '99 4/10 ヴァ− 折り曲げた台形の面積（６）
7/24 a2 が正しいと思います。
というのは、7/6 は 正方形の1辺の長さが2のときの面積なので、
正方形の1辺の長さがaのときの面積は、その a2 /4 倍になるはずですから。
NO.439 '99 4/12 水の流れ 折り曲げた頂点の範囲（１）
太郎さんのお子さんは折り紙が好きです。
ここに、１辺が２cmの正方形の折り紙ＡＢＣＤがあります。
左の図のように、辺ＡＢ、ＡＤ上の点Ｐ、Ｑを折り目として、
３角形ＡＰＱを折ったとき、頂点Ａの来る位置をＫとします。
Ｐ、Ｑがそれぞれ辺ＡＢ、ＡＤ上を自由に動くとき、
点Ｋの動く範囲の面積を求めなさい。
太郎さんも童心にかえって、いろいろと折り曲げて考えることにしました。
皆さんも、考えてください。
＜参考文献：パズルより面白い中学入試の算数）講談社＞
NO.440 '99 4/13 Junko 折り曲げた頂点の範囲（２）
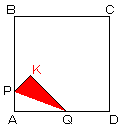
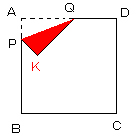
便宜上、上下逆にして考えます。
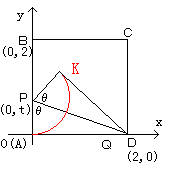
右図のように、点Ａが原点Ｏに、ＡＤ，ＡＢがそれぞれｘ軸、ｙ軸になるように
座標平面上にのせます。
Ｐ、Ｑはそれぞれ辺ＡＢ、ＡＤ上を自由に動くことができますが、
とりあえず点Ｐを固定して、座標をＰ(0,t)とします。
点ＱをＡＤ上で自由に動かすと、点Ｋは、中心Ｐ、半径tの
円の一部(左図の赤い部分)を描きます。
点Ｑが点Ｄと重なった時が限界で、それ以上点Ｋが上に行くことはありません。
∠ＯＰＤ＝∠ＫＰＤ＝θとします。
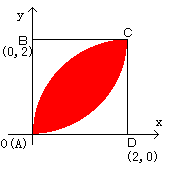
NO.441 '99 4/14 水の流れ ビｭｯフォンの針の実験
昔、ビｭｯフォン（Ｂｕｆｆｏｎ）の針の実験をしたことがあります。
大きな紙に間隔がｄの平行線をたくさん引き、
長さｋの針をばらばらに落としたとき、
針が平行線と交わる確率ｐは
ｐ＝２ｋ／πｄ
となることを証明してください。
実験では、多数の針を落として（もちろん、
針を使ってけがをしないように取り扱ってください）、
次の式からｐを求めます。
ｐ＝（平行線にかかった針の数）÷（落とした針の数）
そこで、皆さん一度試してみてください。
準備するもの。
ｄ＝８ｃｍ 、ｋ＝４ｃｍ のとして、針を千本と大きなビー紙
NO.442 '99 4/16 Junko Math Exercises
「Math Exercises」というペ−ジに行くと、 やさしいものから難しいものまで数学の問題がたくさん用意されています。 すべて英語でかかれていますが、数式は世界共通ですから意味はわかると思います。 まさに、"数学は世界の共通語"です。
解答を送り正解だと名前を載せてもらえます。
いろいろな国の人が参加しています。
様々な国の人と同じ問題に取り組んでいるのだなあと思うと、
これはインタ−ネットの魅力ですね。
NO.443 '99 4/19 プ−太 xn+yn=zn（１）
問題３「らせん階段の問題」のコメント欄に
フェルマ−の最終定理と書かれてあります。
ｎが３以上の自然数の場合、
「xn+yn=zn」を満たす整数x、y、zは存在しない。
（ｎ＝２のときには、ピタゴラス数といって整数解x、y、zは無限に存在し、 その整数解の公式が知られている）
僕が研究した成果は、以下のみです。
ｎが-３のとき、
x-3+y-3=z-3
両辺に(xyz)3をかけて、
(yz)3＋(zx)3=(xy)3
ところが、整数解x、y、zが存在したとすると、フエルマーの大定理に矛盾。
よって、整数解は存在しない。
同様に、ｎが-４以下の整数のときも、整数解は存在しません。
NO.444 '99 4/19 水の流れ 三角形の確率
円周上に３点Ａ，Ｂ，Ｃを任意に選んで、三角形ＡＢＣが 次の三角形になる確率を求めよ。
NO.445 '99 4/20 Junko xn+yn=zn（２）
E-mail
戻る