コロキウム室

ラグラジアンとハミルトニアンン形式に基づく力学の定式化について、一通り頑張ってみます。

1. ラグラジアン形式の力学
   

   １自由度運動に限定します。 この中には、NO.1158の二次元空間の中の1次元曲線に束縛されるような運動も含みます。 要するに運動を表すために、一個の位置座標しか必要ないということです。 それが１自由度の意味です。運動を決定する母関数のようなものを考えます。 それをLとし、ラグラジアンと呼びます。運動を決定するLとはどんなものなのか？　 参考文献［1］の受け売りによれば、
   
   

   運動の各瞬間の位置と速度を全て与えれば、運動は定まる．　(1)
   
   ので、
   
   　　Ｌ＝Ｌ(ｖ、ｘ、ｔ)　　　　　 (2)
   
   で必要十分です。ここでtは時間、xはその時の位置座標，vはその時のその位置での速度。 多くの場合エネルギー保存則が成り立ちます。mを粒子の質量，U(x)を力のポテンシャルとして、
   

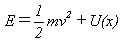   　　　　　　(3)
   
   式(3)は、速度と位置の関係が時間と無関係に定まることを示します。 ラグラジアンLは運動を決めるものなので、(2)が時間tを陽に含むならば、 vとxの関係も時間に依存し(3)は成り立ちません。従ってエネルギー保存則が成立する場合は、
   
   　　Ｌ＝Ｌ(ｖ、ｘ)　　　　　 (4)
   
   です。これを保存系と呼びます。保存系のラグラジアンは、
   

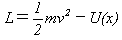   　　　　　　(5)
   
   であり、運動方程式がラグランジュ方程式、
   

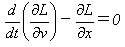   　　　　　　(6)
   
   であることはすぐにわかります。ここで∂L/∂vの意味は 、L(v，x)のvとxを別々の変数とみなしたvでの偏微分の意味で、 その外側のd/dtは、vとxを時間の関数v(t)，x(t)とみての微分です。やります。
   

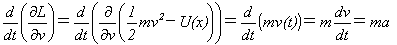   　　　　　　(7)
   
   式(7)の最後のaは、加速度を表します。∂L/∂xも∂L/∂vと同じ意味で、
   

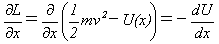   　　　　　　(8)
   
   となり、式(6)は保存系の通常の運動方程式、
   

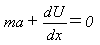   　　　　　(9)
   
   に一致します。通常の座標を使う限り、ラグラジアンを用いる方法はたんに面倒なだけですが、 任意に変換された座標でもラグランジュ方程式(6)がそのままの形で成り立つところに意味があります。 No.1158の最速降下問題を例にとります。通常の（x，y）座標での系の全方程式は以下となります。
   

   　　
   
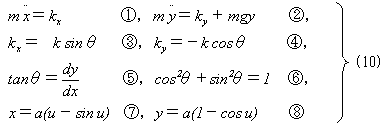
   ここで・は時間に関する微分，kは運動を束縛する最速降下線から、 その内法線方向に粒子が受ける抗力です。未知数の数と条件数を勘定してみると 過不足はありませんが、とても扱い切れそうにありません。
   こうなった理由は、座標（x，y）が独立でないからです。式(10)-�@，�Aは（x，y） に関する運動方程式でこれが解ければ良いのですが、（x，y）が独立でないために（x，y） を関係付ける抗力kが入ってきます。抗力kを束縛曲線の形から定めるために、 その後6本もの式が必要になります（式(10)-�B〜�G）。
   運動が１自由度なのは明らかなので、束縛曲線の形を定める式(10)-�F，�Gのパラメーターuを、 最初から運動の座標にとってやるべきです。式(10)-�F，�Gを出発点にとれば、 ｛（x，ｙ）｝空間で運動軌道が最速降下線になることは自明なので、抗力kは不要です。 x(t)，y(t)が欲しければ、uに関する運動方程式からu＝u(t)を得たあとで、 u(t)を式(10)-�F，�Gへ単に代入するだけでx(t)，y(t)を得られます。実際にやってみます。
   運動エネルギーをT，位置エネルギー（力のポテンシャル）をUとして、式(10)-�F，�Gより、
   

   　　
   
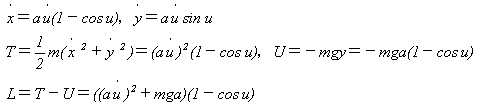
   となりますが、式(6)はどんな座標でも成り立ちます。 1−cos u＝2sin²(u/2)であることに注意して、
   

   　　
   
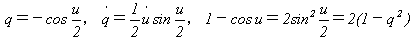
   と変換すると、
   

   　　
   
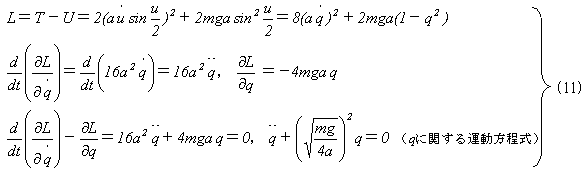
   となり、qに関する単振動の式が現れます。 ここから最速降下線振り子の等時性や振動周期は一気に片づきますが、 この変換はNO.1160のyokodonさんを見て気づきました（超有名題なのでたぶん常識）。 問題が解けてしまえば作用変数もクソもありません。 最適な変数変換や置換に関して、人間の目に優るものはありません・・・。 そして最適な変数が選ばれた時、ラグラジアン形式はすごい威力を発揮します、 と苦しい言い訳をするしかありません・・・苦しいよ〜〜。
   もちろんqに関する運動方程式は、式(10)からよけいな未知数を順次消去して同じ変換を行っても 得られるはずですが、明らかに非常に難儀です。少しでも問題が複雑になると、 運動方程式を立てるのすら困難になる場合は多々あります。 それに対してラグラジアンを用いた式(11)の方法では、微分計算と、 変数を書きかえる代入計算だけでことは済みます。この2つはやれば必ずできるものです。 また1自由度以上の多自由度運動や連続体力学まで考えれば、 ラグラジアン形式は手放せなくなります。
   ラグランジュ方程式(6)が任意の座標変換で形を変えないことは、通常の座標xが、
   
   　　ｘ＝ｘ(ｑ、ｔ)　　　　　 (2)
   
   と一般化座標qに変換されたとして、速度dx/dtを一般化速度dq/dtによって表わした、
   

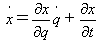   　　　　　(13)
   
   などを式(6)に直接代入して示すこともできますが、 もっと重要なことは、式(6)が変分原理を導くことです。
   式(6)は、NO.1150-[4]のオイラーラグランジュ方程式と全く同じものです。 それは同式で、y → x，y' → v，微分ﾊﾟﾗﾒｰﾀｰとしてx → tと読みかえれば明らかです。 よってNO.1150-[3]よりラグランジュ方程式(6)は、定積分、
   

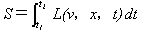   　　　　　(14)
   
   を最小化するものです。定積分Sは作用積分と言われ、 作用積分を最小化してラグランジュ方程式から運動方程式を導くことを、 最小作用の原理と言います。オイラーラグランジュ方程式は、 Lの具体的関数形に依存していません。従ってそれがどのような座標で書かれていようと 常に同じ形になり、そのとき定積分(14)は最小になります。 よってラグランジュ方程式(6)は、任意の座標で不変です。 また式(14)のLが時間tを陽に含んでも良いことから、 最小作用の原理は保存系以外の運動にも成り立ちます。
   
   

2. ハミルトン形式の力学
   ラグラジアン形式は、運動方程式を座標の2階微分方程式として与えます（式(11)の最下段のように）。 2階微分方程式は、1階の連立微分方程式に分解できます。2階微分方程式としての運動方程式を、 運動の解析に特に適した形で、系統的に連立1階微分方程式へ分解する方法が、ハミルトン形式です。 参考文献[2]の受け売りをすれば「そのようなことをしても物理的に新しい内容がつけ加わるわけ ではない」のですが「理論的見通しが良く」なります。 プロではないので「理論的見通し」の効果について、即座に適当な例は出てきません。 そこで我田引水な感覚でいうと、少なくとも式(10)と(11)くらいの違いはあります。
   

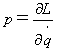   　　　　　(15)
   
   で一般化運動量pを定義します。ここでラグラジアンLは、L＝L(dq/dt，q，t)です。 pが運動量と呼ばれるのは式(5)，(6)より、通常の座標では∂L/∂v＝mvで運動量p＝mvだからです。 式(15)で式(6)を書きかえると運動方程式は、
   

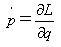   　　　　　(16)
   
   となります。いまのところ運動を決定するのはラグラジアンなので、 Lから出発してハミルトン形式を導きます。L＝L(dq/dt，q，t)の全微分をとります。
   

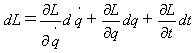   　　　　　(17)
   
   式(17)に(15)，(16)を代入し、
   

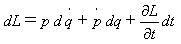   　　　　　(18)
   
   を得ます。式(18)の右辺第1項を、積の微分公式、
   

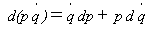   　　　　　(19)
   
   を利用して消去します。
   

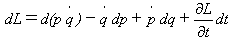   　　　　　(20)
   
   式(20)の右辺第1項を左辺へ移項し、全体の符号を変えれば、
   

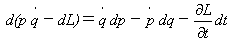   　　　　　(21)
   
   が得られます。以上の変形の目的はこうです。 運動方程式を連立1階微分方程式に分解する最も単純な方法は、 式(15)，(16)で（p，q）を通常の運動量，座標とすれば明らかですが、
   

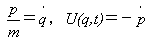   　　　　　(22)
   
   とすることです。しかしこの形は任意の座標で不変ではありません。 そこでラグラジアン形式を利用して、任意の座標で不変な分解法を得ることが目的です。 ただし式(22)の未知数は、速度dq/dtと座標qではなく、運動量pと座標qとみなすべきです。 dq/dtはたんに座標qの時間微分として微分方程式の中に現れただけです。 いいかえれば式(22)の目的は、2つの未知関数p(t)とq(t)を求めることです。 それが分解の意味です。従ってラグラジアンLを（p，q，t）の関数に変形する必要があります。 しかもそれは運動方程式(15)，(16)の組を満たす必要があります。 Lの全微分を持ち出したのは、式(15)，(16)にLの偏微分が出てくるからです。 またLの全微分から不要な未知数の微分であるd(dq/dt)を消去して、 dq/dtを含まないLの変形を与えることが、式(19)の最大の目的です。 式(21)の右辺は何らかの関数の（p，q，t）に関する全微分になっています。 よって(21)の左辺は、dH(p，q，t)とおけます。H(p，q，t)の全微分を正直に書いてやれば、
   

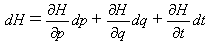   　　　　　(23)
   
   が得られます。式(23)と(21)の右辺の係数を比較することにより、
   

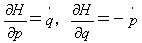   　　　　　(24)
   
   となります。式(24)をハミルトン方程式または正準方程式といい、Hをハミルトニアンと呼びます。 ハミルトン方程式の導出は、座標変換に対して不変な関係式(15)，(16)と 恒等式(17)，(19)，(23)のみ用いたので、任意の座標で不変です。 式(15)，(16)を使っているので、式(24)は運動方程式の成立する必要条件です。 十分条件でもあることは、通常の座標と運動量でエネルギーEをE＝p²/2m＋U(q，t)と書き直し、 H＝E(p，q，t)とおいて(24)に代入すれば式(22)が得られ、 (24)が任意の座標で不変な関係であることから明らかです。 従ってハミルトニアンHはエネルギーEに等しくなります （一般には保存しませんし、式(15)をdq/dtについて解いたのち、 (p，q，t)で表したdq/dtを用いてE(dq/dt，q，t)をE(p，q，t)に書き直す必要もあります）が、 このことはふつう、式(21)の左辺を式(15)を用いて一般化座標qで書き下し、 直接代入計算して示されます。
   ここでのハミルトン方程式の誘導は主に参考文献[1]に従いました（一番とっつき易い思われます）。 定式化としては他に、式(21)の左辺のｄ()内を直接ハミルトニアンの定義とする方法もあります。 これをルジャンドル変換といい、参考文献[2]ではこれを採用しています。 参考文献[5]では、ルジャンドル変換の数学的意味と目的，ラグラジアンに対するハミルトニアン の正体を、最も明快に与えてくれたと思われますが、私には難かし過ぎました （ベクトル束の余接バンドルへの変換？）。 参考文献[4]は、同じことをもっと初等的に説明してくれましたが、 逆に意味の明瞭さが失われたと思います。以上、個人的感想でした。
   式(24)は任意の座標変換よりも広い変換、
   
   　　ｑ＝ｑ(Ｐ,Ｑ,ｔ)，ｐ＝ｐ(Ｐ,Ｑ,ｔ　　　　　 (25)
   
   に対して不変性を持っています。ここで（P，Q）は新しい一般化運動量と一般化座標です。 ただし完全に任意ではなく制約条件が付きます。 (24)の形を不変に保つ一般化運動量と一般化座標の定め方が、正準変換論です。 正準方程式の名はそこから来てますが、正準変換を求めるときにも変分原理が必要になります。 それは式(14)の適当な変形から得られます。 またこのとき一般化運動量と一般化座標は正準共役量と呼ばれます。 NO.1158の作用−角変数は正準共役量の一つで、定義自体は正準変換の一応用にすぎませんが、 本来は正準変換を利用した摂動論用に開発されたものです（ということを知ってるだけです。 本の目次を見ればわかりますから・・・）。これ以上頑張ると大嘘を書きそうなので、 最後に参考文献をあげて終わります。

参考文献
[1]力学，ランダウ=リフシッツ，東京書店．
[2]古典力学，ゴールドスタイン，吉岡書店．
[1][2]は少々古いかもしれませんが、世界中で最も愛された（？）標準的テキストと思います。
[3]解析力学，大貫義郎，岩波書店．
[1][2]の解析力学関連のエッセンスが解説されてます。
[4]古典力学の数学的方法，アーノルド，岩波書店．
すでに現代風古典力学の現代的古典だと思います。個人的には多様体のﾁｬｰﾄとｱﾄﾗｽで挫折しました。
[5]数学−その形式と機能，マックレーン，森北出版．
力学関係以外にも、読んで損はない本と思いますが、分厚いのと高額なのが食指を遠ざけます。

第９３回数学的な応募問題

太郎さんは最近、大学入試問題を解く機会が増えています。 命題と論理のところで、下のような問題を解いたことがあります。

−３≦ｘ≦３の範囲で、２つの関数　ｆ（ｘ）＝ｘ^２＋２ｘ−２　， 　　ｇ（ｘ）＝−ｘ^２＋２ｘ＋ａ＋１　について、
次の命題が成り立つようなａの範囲をそれぞれ求めよ。

問１：すべてのｘに対して　，　ｆ（ｘ）＜ｇ（ｘ）

問２：あるｘに対して　，ｆ（ｘ）＜ｇ（ｘ）　

問３：すべての値 ｘ_１　，ｘ_２　に対して　， ｆ（ｘ_１）＜ｇ（ｘ_２）

問４：ある値 ｘ_１　，ｘ_２　に対して　，ｆ（ｘ_１）＜ｇ（ｘ_２）
　

　　<問題の出典：平成１０年大阪教育大学の入試問題で改題＞

問１
Ｆ(ｘ)＝ｇ(ｘ)−ｆ(ｘ)＝−２ｘ^２＋ａ＋３とおく。
これは上に凸の放物線で、頂点の座標は、(０，ａ＋３)となる。
−３≦ｘ≦３を満たすすべてのｘに対して、Ｆ(ｘ)＞０となっていればよい。
そのためには、−３≦ｘ≦３におけるＦ(ｘ)の最小値、Ｆ(３)＝Ｆ(−３)＝ａ−１５＞０であればよい。
従って、ａ＞１５

問２
−３≦ｘ≦３を満たすあるｘに対して、Ｆ(ｘ)＞０となっていればよい。
そのためには、−３≦ｘ≦３におけるＦ(ｘ)の最大値、Ｆ(０)＝ａ＋３＞０であればよい。
従って、ａ＞−３

問３
ｆ(ｘ)＝(ｘ＋１)^２−３より、下に凸の放物線で、頂点の座標は、(−１，−３)
−３≦ｘ≦３における
最大値　ｍａｘ_ｆ＝ｆ(３)＝１３
最小値　ｍｉｎ_ｆ＝ｆ(−１)＝−３

ｇ(ｘ)＝−(ｘ−１)^２＋ａ＋２より、上に凸の放物線で、頂点の座標は、(１，ａ＋２)
−３≦ｘ≦３における
最大値　ｍａｘ_ｇ＝ｇ(１)＝ａ＋２
最小値　ｍｉｎ_ｇ＝ｇ(−３)＝ａ−１４

題意を満たすためには、ｍａｘ_ｆ＜ｍｉｎ_ｇであればよい。
つまり、１３＜ａ−１４
　　　　　２７＜ａ

問４
題意を否定すると以下のようになる。

「すべての値 ｘ_１　，ｘ_２　に対して　， ｆ（ｘ_１）≧ｇ（ｘ_２）」

下のグラフは、「GRAPES」で ｆ（ｘ）＝ｘ^２＋２ｘ−２と ｇ（ｘ）＝−ｘ^２＋２ｘ＋ａ＋１を描いたものです。
パラメーターａは初期値ａ＝１となっていますが、その場で アニメーションのように変更ができます。
授業で生徒に説明する際にこれを使ってみたら、よりいいのではないかと思います。

問１
F(x)＝g(x)−f(x) とすると
F(x)＝−2x²＋a＋3
すべてのxに対してF(x)＞０となるためにはF(−3)＞０かつF(3)＞０である
(対称性を考えて片方だけでよい)
F(3)＝−18＋a＋3＞０　　 ∴ a＞15

問２
F(x)＝−2x²＋a＋3＞０となるxが１つでも存在すればよいので
a＋3＞０　　 ∴ a＞−3

問３
f(x)＝(x＋1)²−3　 g(x)＝−(x−1)²＋a＋2
−3≦x≦3 において f(x)の最大値＜g(x)の最小値 となればよい
つまり 13＜a−14　　 ∴ a＞27

問４
−3≦x≦3 において f(x)の最小値＜g(x)の最大値 となればよい
つまり −3＜a＋2　　 ∴a＞−5

５５の９９乗は解るんですが９９の！の！がどういう意味なのか 全く解りません。明日にでも調べて見ようと思いますが よかったら、教えてくれませんか？

「９９！」は「９９の階乗」と読みます。
冗談みたいな話ですが、あまりに大きい数なのでびっくりマーク（？）
定義はこうです。
「９９！＝９９×９８×９７×・・・３×２×１」 となります。
つまりその自然数から始まって、１減らしながら最後の１までずべ ての積をとるわけです。

大学の解析学初歩で有名なダ・ランベールの判定法：
「


が、０≦ｒ＜１なら収束、＝１なら判定不能、＞１なら発散」 がありますが、

　　(訂正3/7,20:30,Junko)

には役立っても、以下のような級数に適用しては、判定不能 となってしまいます。

これらの収束発散を言い当てることのできる、実用的な判 定法は見つかっているのでしょうか？（収束値の求値では なく、収束の有無の判定）
また、上記でｒ＝１となる級数には、どのような性質が備 わっているのでしょうか？

判定法というわけではないのですが、 単調減少関数fに対して

が成り立ちます。実際

というわけで Σf(n)の収束、発散は∫f(t)dtのそれに帰着されます。

模試シリーズ9

曲線Ｃ：y ＝ ax³ + bx² +cx（a ≠ 0）上に異なる２点Ｐ，Ｑを、次の条件を満 たすようにとることが出来るための、実数 a，b，c の満たすべき条件を求めよ。

条件：Ｐ，ＱにおけるＣの接線は平行である。また、Ｐにおける接線を l とし、 直線 y ＝ x に関して l と対称な 直線を l' とするとき、l' と直線ＰＱは直交する。

階乗に派生したコンピュータプログラムの話題ということで。 かなり古いものですが、コンピュータ雑誌「ｂｉｔ」（Ｖｏｌ．１ ５、Ｎｏ．４）に、組み合せの数をなるべく桁溢れせず求められる か？という興味深い話題が出ていたのでご紹介しておきます。 組み合せの数は「１３人のアイドルグループから４人で構成される サブグループを作る組み合せ」というような数を計算するときに登 場します。
ｍ個からｎ個を選ぶ組み合せの数は

　　_ｍＣ_ｎ

と略記して

　　　ｍ！／｛（ｍ−ｎ）！ｎ！｝＝｛ｍ（ｍ−１）…（ｍ−ｎ＋１）｝／ｎ！

　　　　(訂正3/10、20:00)

で求められますが、コンピュータで手作りのプログラムで求めよう とする場合、このままの式を使うと、一般に分子も分母も巨大な数 になるため、ちょっと大きなｍやｎを与えると、「結果」が桁溢れ しないはずなのに、計算の「途中」で数値が簡単に桁数オーバーし てしまいます。

　　_ｍＣ_ｎ＝_ｍＣ_ｍ−ｎ

の利用だけでは、本質的に桁溢れの解決になりませんし、

　　_ｍＣ_ｎ＝_ｍ−１Ｃ_ｎ−１＋_ｍ−１Ｃ_ｎ

では、計算量（計算時間）が大変多くかかってしまいます。
でも、よくよく考えると組み合せの数は整数ですからｍ（ｍ−１）…（ｍ−ｎ＋１）は は必ずｎ！で割り切れるはずです。
というわけで、件の記事には機械的に組み合せの数の分数の部分を 完全に約分しきれる素晴らしいプログラムが掲載されています。以 下は元記事がfortranで記述されていたものを本質部分だけ私がcに 書き直したものです（unsigned longで 21億が表現できるマシンで あれば₃₂Ｃ₁₆までは求めることが可能です）。

◆組み合せの数の約分完遂による求値方法

unsigned long combi(unsigned long m,unsigned long n) {

    unsigned long      p,c ;
    unsigned long      bunbo[17],bunsi[17] ;
    unsigned short     i,k ;
    short              j ;

    p = (n < m-n)?n:(m-n) ;
    c = 1 ;
    for(i=1;i<=p;i++) {         /* expand */

        bunsi[i] = m-p+i ;
        bunbo[i] = i ;
    }
    for(k=2;k<=p;k++) {         /* reduce */

        j = -((m-p)%k) ;
        for(i=k;i<=p;i+=k) {

            bunsi[i+j] /= bunbo[k] ;
            bunbo[ i ] /= bunbo[k] ;
        }
    }
    for(i=1;i<=p;i++) {         /* multiply */

        c *= bunsi[i] ;
    }
    return(c) ;
}

◆約分の様子（₁₆Ｃ₈ の例）

        9 *10 *11 *12 *13 *14 *15 *16
16Ｃ8 = -----------------------------    expand
        1 * 2 * 3 * 4 * 5 * 6 * 7 * 8

        9 * 5 *11 * 6 *13 * 7 *15 * 8
  　　= -----------------------------    reduce k=2,j=0
        1 * 1 * 3 * 2 * 5 * 3 * 7 * 4

        3 * 5 *11 * 2 *13 * 7 *15 * 8
 　　 = -----------------------------    reduce k=3,j=-2
        1 * 1 * 1 * 2 * 5 * 1 * 7 * 4

        3 * 5 *11 * 1 *13 * 7 *15 * 4
 　 　= -----------------------------    reduce k=4,j=0
        1 * 1 * 1 * 1 * 5 * 1 * 7 * 2

        3 * 1 *11 * 1 *13 * 7 *15 * 4
　  　= -----------------------------    reduce k=5,j=-3
        1 * 1 * 1 * 1 * 1 * 1 * 7 * 2

        3 * 1 *11 * 1 *13 * 7 *15 * 4
　  　= -----------------------------    reduce k=6,j=-2
        1 * 1 * 1 * 1 * 1 * 1 * 7 * 2

        3 * 1 *11 * 1 *13 * 1 *15 * 4
 　 　= -----------------------------    reduce k=7,j=-1
        1 * 1 * 1 * 1 * 1 * 1 * 1 * 2

        3 * 1 *11 * 1 *13 * 1 *15 * 2
      = -----------------------------    reduce k=8,j=0
        1 * 1 * 1 * 1 * 1 * 1 * 1 * 1

      = 3 * 1 *11 * 1 *13 * 1 *15 * 2    multiply

      = 12870

E-mail 戻る