Weekend Mathematics／問題／問題34

３４．三角形の問題


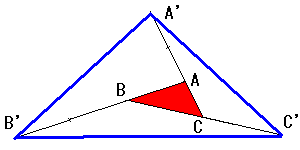
左の図のように△ＡＢＣの各辺を一定方向に延長して△Ａ'Ｂ'Ｃ'を作る。
そして、ＡＣ：Ａ'Ｃ＝１：３、ＢＣ：ＢＣ'＝１：２、ＡＢ：ＡＢ'＝１：３です。
この時△Ａ'Ｂ'Ｃ'の面積は△ＡＢＣの面積の何倍になるでしょう。





問題の出典


ピ−タ−・フランクルの算数名問題

ピ−タ−・フランクル

講談社






答えと解説












答えと解説

解答・その１

（ペンネ−ム：海津北高校１年情報処理科）


△ＡＢＣの面積をＳとおくと、
ＢＣ＝ＣＣ’より△ＡＣＣ’＝Ｓ
ＡＡ’＝２ＣＡより△ＡＡ’Ｃ’＝２Ｓ
ＡＡ’＝２ＣＡより△ＡＡ’Ｂ＝２Ｓ
ＢＢ’＝２ＡＢより△Ａ’Ｂ’Ｂ＝４Ｓ
ＢＢ’＝２ＡＢより△ＢＢ’Ｃ＝２Ｓ
ＢＣ＝ＣＣ’より△Ｂ’ＣＣ’＝２Ｓ
よって、△Ａ’Ｂ’Ｃ’＝１４Ｓ
すなわち、１４倍（答）




解答・その２

（ペンネ−ム：ちゃめ）


三角形ABC'で、BC：CC'＝１：１だから、
三角形ABC：三角形ACC'＝１；１　・・・（１）
三角形A'CC'で、AC：A'A＝１：２だから、
三角形ACC'：三角形A'AC'＝１：２　・・・（２）
三角形A'BCで、AC：A'A＝１：２だから、
三角形ACB：三角形A'AB＝１：２　・・・（３）
三角形A'B'Aで、AB：BB'＝１：２だから、
三角形A'AB：三角形A'BB'＝１：２　・・・（４）
三角形AB'Cで、AB：BB'＝１：２だから、
三角形ABC：三角形BB'C＝１：２　・・・（５）
三角形B'BC'で、BC：CC'＝１：１だから、
三角形B'BC：三角形B'CC'＝１：１　・・・（６）
（１）より、
三角形ACC'＝三角形ABC　・・・（７）
（２）、（７）より、
三角形A'AC＝２×三角形ABC　・・・（８）
（３）より、
三角形A'AB＝２×三角形ABC　・・・（９）
（４）、（９）より、
三角形A'BB'＝４×三角形ABC　・・・（１０）
（５）より、
三角形BB'C＝２×三角形ABC　・・・（１１）
（６）、（１１）より、
三角形B'CC'＝２×三角形ABC　・・・（１２）

三角形A'B'C'＝三角形ABC＋三角形ACC'＋三角形A'AC＋三角形A'AB＋三角形A'BB'＋三 角形BB'C＋三角形B'CC'
だから、（７）、（８）、（９）、（１０）、（１１）、（１２）より、 三角形A'B'C'＝１４×三角形ABC
よって三角形A'B'C'の面積は三角形ABCの面積の１４倍　・・・（答え）




解答・その３

（ペンネ−ム：sambaGREEN）


△ＡＢＣの面積をＳとすると，
△ＡＡ’Ｂ＝２Ｓ　，　△ＣＡ’Ｂ＝３Ｓから △ＡＡ’Ｂ’＝６Ｓ　，　△Ｃ’Ａ’Ｃ＝３Ｓ
また△ＣＢＢ’＝２Ｓから　△Ｃ’ＢＢ’＝４Ｓ
したがって，△Ａ’Ｂ’Ｃ’＝Ｓ＋６Ｓ＋３Ｓ＋４Ｓ＝１４Ｓ
全部１：３なら，対称性から，Ｓ＋６Ｓ×３＝１９Ｓで，もっと楽なのにね





解答・その４

（ペンネ−ム：小春）


ＡＢ：ＢＢ’＝１：Ｌ、ＣＡ：ＡＡ’＝１：Ｍ、ＢＣ：ＣＣ’＝１：Ｎ、 三角形ＡＢＣの面積を１と、すると、
三角形ＡＢＣと三角形ＡＢＡ’は、高さが同じで、底辺がの比が、１：Ｍになっているので、
三角形ＡＢＣ：三角形ＡＢＡ’＝１：Ｍ　より、三角形ＡＢＡ’の面積はＭ
同じように、ＡＢＡ’：ＢＢ’Ａ’＝１：Ｌ　より、三角形ＢＢ’Ａ’の面積はＭＬ
　　　　　　ＡＢＣ　：ＡＣＣ’　＝１：Ｎ　より、三角形ＡＣＣ’の面積はＮ
　　　　　　ＡＢＣ’：ＢＢ’Ｃ’＝１：Ｌ　より、三角形ＢＢ’Ｃ’の面積はＬ（１＋Ｎ）
　　　　　　ＡＣＣ’：ＡＣ’Ａ’＝１：Ｍ　より、三角形ＡＣ’Ａ’の面積はＭＮ
以上から全ての面積を足すと、
１＋Ｍ＋ＭＬ＋Ｎ＋Ｌ（１＋Ｎ）＋ＭＮ　＝　（Ｌ＋１）（Ｍ＋１）（Ｎ＋１）ーＬＭＮ
ここで、Ｌ＝２、Ｍ＝２、Ｎ＝１を代入すると、
三角形Ａ’Ｂ’Ｃ’の面積は１４となるので、 求める答えは三角形ＡＢＣの１４倍に、なると思います。




解答・その５

（ペンネ−ム：少年Ｈ）


△ABCにおいて AB=c,BC=a,CA=b,∠CAB＝A,∠ABC=B,∠BCA＝Cとすると
△ABCの面積は



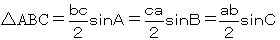
△ＡＡ'Ｂ'において、ＡＡ'＝2ｂ,Ｂ'Ａ＝3ｃ,∠Ｂ'ＡＡ'＝π−Ａであるから
△ＡＡ'Ｂ'の面積は



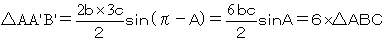
同様に



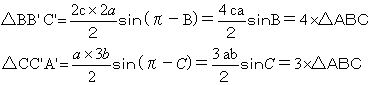
よって△Ａ'Ｂ'Ｃ'＝△ＡＡ'Ｂ'＋△ＢＢ'Ｃ'＋△ＣＣ'Ａ'＋△ＡＢＣ
＝（６＋４＋３＋１）△ＡＢＣ
＝1４ △ＡＢＣ

答え １４倍




解答・その６

（ペンネ−ム：浜田　明巳）

今回はVisual Basicで解答プログラムを作ってみました．
プログラムの内容は以下の通りです． 乱数を使い３点Ａ，Ｂ，Ｃの座標を決定し，３点Ａ'，Ｂ'，Ｃ'の座標を求め， ヘロンの公式を使い，△ＡＢＣ，△Ａ'Ｂ'Ｃ'の面積を計算し， 比△Ａ'Ｂ'Ｃ'／△ＡＢＣを計算する． Ａ，Ｂ，Ｃの座標を少しずつ動かし，それぞれの場合の比を計算する． この試行を全部で５００回繰り返し，比の平均を求める．
このプログラムにより，答は１４になる事が分かります．

Option Explicit
Sub Form_Load()
    Picture1.Scale (0, 0)-(1, 1)
End Sub
Sub Command1_Click()
    '三角形の問題
    Randomize Timer
    Dim j1, j2, j3, j4, j, jj, iro, iro0, iro1, iro2 As Integer
    iro0 = RGB(255, 255, 0): iro1 = RGB(0, 0, 255)
    iro2 = RGB(255, 0, 0)
    Dim shikoukaisuu, kaisuu, machijikan As Long
    shikoukaisuu = 500: kaisuu = 0: machijikan = 400000
    Dim x(1, 5), d(1, 2), hen(2), s, menseki(1), wa, hi As Double
    Dim s_genkai, d_genkai, hi_genkai As Double
    wa = 0: s_genkai = 0.2: d_genkai = 0.005: hi_genkai = 10 ^ (-12)
    Dim ten(5) As String
    ten(0) = "A": ten(1) = "B": ten(2) = "C"
    For j1 = 0 To 2: ten(j1 + 3) = ten(j1) + "'": Next
    Picture3.Cls: Picture4.Cls
    For j1 = 0 To shikoukaisuu
     For j2 = 0 To 2
      For j3 = 0 To 1
       If j1 = 0 Then
        x(j3, j2) = Rnd * s_genkai + 0.5
        d(j3, j2) = (Rnd * 2 - 1) * d_genkai
       Else
        d(j3, j2) = d(j3, j2) + (Rnd * 2 - 1) * d_genkai
        If Abs(d(j3, j2)) > d_genkai Then
         d(j3, j2) = -Sgn(d(j3, j2)) * d_genkai
        End If
        x(j3, j2) = x(j3, j2) + d(j3, j2)
        If Abs(x(j3, j2) - 0.5) > s_genkai Then
         x(j3, j2) = 0.5 + Sgn(x(j3, j2) - 0.5) * s_genkai
        End If
       End If
      Next
     Next
     For j2 = 0 To 2
      j = (j2 + 2) Mod 3: jj = -3 * (j2 < 2) - 2 * (j2 = 2)
      For j3 = 0 To 1
       x(j3, j2 + 3) = jj * x(j3, j2) - (jj - 1) * x(j3, j)
      Next
     Next
     For j2 = 0 To 1: s = 0
      For j3 = 0 To 2
       j = j3 + 3 * j2: jj = ((j3 + 1) Mod 3) + 3 * j2: hen(j3) = 0
       For j4 = 0 To 1
        hen(j3) = hen(j3) + (x(j4, j) - x(j4, jj)) * (x(j4, j) - x(j4, jj))
       Next
       hen(j3) = Sqr(hen(j3)): s = s + hen(j3)
      Next
      s = s * 0.5: menseki(j2) = s
      For j3 = 0 To 2
       menseki(j2) = menseki(j2) * (s - hen(j3))
      Next
     Next
     Picture1.Cls
     For j2 = 0 To 3 Step 3: iro = -iro2 * (j2 = 0) - iro1 * (j2 = 3)
      Picture1.PSet (x(0, j2), x(1, j2)), iro
      For j3 = 2 + j2 To j2 Step -1
       Picture1.Line -(x(0, j3), x(1, j3)), iro
      Next
     Next
     For j2 = 0 To 2
      Picture1.Line (x(0, j2), x(1, j2))-(x(0, j2 + 3), x(1, j2 + 3)), iro0
     Next
     For j2 = 0 To 5
      Picture1.CurrentX = x(0, j2): Picture1.CurrentY = x(1, j2)
      Picture1.Print ten(j2)
     Next
     Picture2.Cls: Picture2.Print j1; "回試行"
     If menseki(0) >= hi_genkai Then
      For j2 = 0 To 1: menseki(j2) = Sqr(menseki(j2)): Next
      hi = menseki(1) / menseki(0): wa = wa + hi: kaisuu = kaisuu + 1
      Picture3.Cls: Picture3.Print "△A'B'C'/△ABC="; hi
      Picture4.Cls: Picture4.Print "平均                ="; wa / kaisuu
     End If
     For j2 = 0 To machijikan: Next
    Next
    Beep
End Sub
Private Sub Command2_Click()
    End
End Sub




正解者

かに海津北高校１年情報処理科小春
浜田　明巳少年Ｈマサボ−
tokisambaGREENch3cooh
ちゃめうにうに





まとめ

三角形の面積Ｓを求めるための公式は、 Ｓ＝(1/2)･(底辺)･(高さ)です。
ですから、底辺を同じにして高さをｍ倍すれば面積もｍ倍となります。
逆に高さを同じにして底辺をｎ倍すれば面積もｎ倍となります。
同時に高さをｍ倍、底辺をｎ倍すれば面積はｍｎ倍となります。
三角形A'B'C'を適当に分割し、上述のことを用いれば答えはでるかなと思います。

解答・その４で「小春」さんが示してくださったように一般に、 ＡＢ：ＢＢ’＝１：Ｌ、ＣＡ：ＡＡ’＝１：Ｍ、ＢＣ：ＣＣ’＝１：Ｎとすると、
面積は、(Ｌ＋１)(Ｍ＋１)(Ｎ＋１)ーＬＭＮ 倍となります。
さらに解答・３で「sambaGREEN」がおっしゃっているようにすべて同じ比ならもっとsimpleになります。
Ｌ＝Ｍ＝Ｎですから面積は、(Ｌ＋１)3ーＬ3　倍となります。


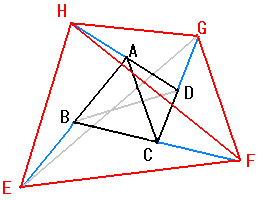
「ピ−タ−・フランクルの算数名問題」には、これの立体版が載っています。

左の図のように４面体ＡＢＣＤの各辺を各々２倍に延長して４面体ＥＦＧＨを作る。 このとき、ＥＦＧＨの体積は、ＡＢＣＤの体積の何倍になるでしょうか？
というものです。


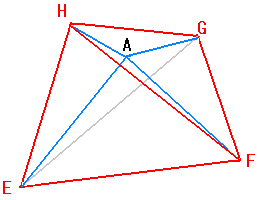
これはむずかしい・・・！！
上記の本からかいつまんで解答を引用させてもらいます。
元の４面体ＡＢＣＤの頂点から１点Ａを選び、ＥＦＧＨの各頂点と結びます。
すると、４面体ＥＦＧＨを４つの４面体、Ａ-ＥＦＧ，Ａ-ＥＧＨ，Ａ-ＦＧＨ，Ａ-ＥＦＨに分割することができます。
それぞれの体積が４面体ＡＢＣＤの体積の何倍になるかを考えていきます。
４面体の体積は、Ｓ＝(1/3)･(底面積)･(高さ)ですから、底面積･高さに比例します。

  1. ４面体Ａ-ＥＦＧ
    △ＢＦＧの面積は△ＢＣＤの４倍なので、４面体ＡＢＦＧの体積は４面体ＡＢＣＤの４倍。
    △ＡＥＧの面積は△ＡＢＧの２倍なので、４面体ＡＥＦＧの体積は４面体ＡＢＦＧの２倍、 つまり４面体ＡＢＣＤの８倍。

  2. ４面体Ａ-ＥＧＨ
    △ＡＧＨを底面と考えると、高さはＥＡ：ＢＡ＝２：１より４面体ＡＢＧＨの２倍。
    更に、５点Ｈ、Ｇ、Ａ、Ｃ、Ｄは同一平面上にあり、この平面を見ると、 △ＡＧＨの面積と△ＡＣＤの面積は等しいことがわかる。
    従って、４面体ＡＥＧＨの体積は、４面体ＡＢＣＤの体積の２倍。

  3. ４面体Ａ-ＦＧＨ
    ４面体ＡＦＧＨも△ＡＧＨを底面だと考えると、高さはＢＣ：ＣＦ＝１：１より、 体積は４面体ＡＢＣＤと同じ。

  4. ４面体Ａ-ＥＦＨ
    ４面体ＡＥＦＨについては、底面を△ＡＥＦと考えれば、この面積は△ＡＢＣの面積の４倍。
    高さについては、ＨＡ：ＡＤ＝１：１なので１倍。
    つまり４面体ＡＥＦＨの体積は４面体ＡＢＣＤの４倍。

以上のことから、８＋２＋１＋４＝１５　ということで１５倍という結論になります。
しかしながら、図形に弱い(頭の中でイメ−ジできない)私としてはかなりつらい・・・。


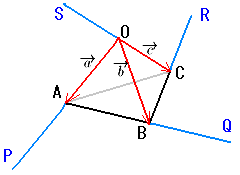
もう１つ１次変換を使った別解も示されていました。
これならばっちり、ということでやってみます。
左図のように各点の名称を付け直します。


となります。 この行列の行列式は |A|=12+1-(-2)=15 となりますので、１５倍というわけです。

これを一般化するのは簡単です。


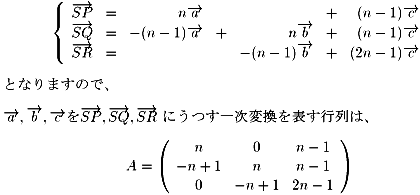
となります。 この行列の行列式は
|A|=n2(2n-1)+(-n+1)2(n-1)-n(n-1)(-n+1)= 4n3-6n2+4n-1 となります。
従って、体積は(4n3-6n2+4n-1)倍となります。

複雑な立体図形を頭の中に描くことのできる人や、 素晴らしいアイディアがぱっと浮かぶような天才、秀才ならともかく、 凡人にとっては、こういう地道な計算で解答にたどり着けるというのはうれしいことです。
計算をばかにしてはいけません。しっかりと基礎力をつけておくのは大切なことです・・・。


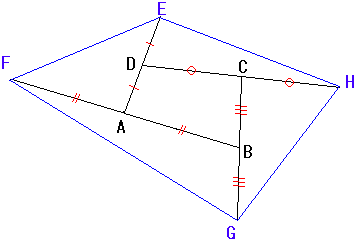
さて、もう１つ発展問題です。
三角形ではなく四角形ではどうでしょう？
つまり左の図のように、四角形ＡＢＣＤの各辺をそれぞれ１方方向に２倍に延長して 四角形ＥＦＧＨを作ります。
この時、四角形ＥＦＧＨの面積は、もとの四角形ＡＢＣＤの面積の何倍になるでしょうか？
出典：「パズルよりおもしろい中学入試の算数」

是非解答をお寄せください。

→　コロキウム室　NO.646　、　NO.651　、　 NO.655　、　NO.656




E-mail 戻る