Weekend Mathematics／コロキウム室／1999.10〜12／NO.75

十進ベーシックでプログラミングしました。
２進モードで解かせた方がやや速いようです。
所要時間　１０分２０〜３８秒。
所要時間にバラツキがあるのは、タイミングによるのでしょうか？。

2	6 7 2 9	1 3 4 5 8
	6 7 9 2	1 3 5 8 4
	6 9 2 7	1 3 8 5 4
	7 2 6 9	1 4 5 3 8
	7 2 9 3	1 4 5 8 6
	7 3 2 9	1 4 6 5 8
	7 6 9 2	1 5 3 8 4
	7 9 2 3	1 5 8 4 6
	7 9 3 2	1 5 8 6 4
	9 2 6 7	1 8 5 3 4
	9 2 7 3	1 8 5 4 6
	9 3 2 7	1 8 6 5 4
3	5 8 2 3	1 7 4 6 9
	5 8 3 2	1 7 4 9 6
4	3 9 4 2	1 5 7 6 8
	4 3 9 2	1 7 5 6 8
	5 7 9 6	2 3 1 8 4
	7 9 5 6	3 1 8 2 4
5	2 6 9 7	1 3 4 8 5
	2 7 6 9	1 3 8 4 5
	2 9 3 7	1 4 6 8 5
	2 9 6 7	1 4 8 3 5
	2 9 7 3	1 4 8 6 5
	3 2 9 7	1 6 4 8 5
	3 7 2 9	1 8 6 4 5
	6 2 9 7	3 1 4 8 5
	7 6 2 9	3 8 1 4 5
	9 2 3 7	4 6 1 8 5
	9 6 2 7	4 8 1 3 5
	9 7 2 3	4 8 6 1 5
6	2 9 4 3	1 7 6 5 8
	4 6 5 3	2 7 9 1 8
	5 6 9 7	3 4 1 8 2
7	2 3 9 4	1 6 7 5 8
	2 6 3 7	1 8 4 5 9
	4 5 2 7	3 1 6 8 9
	5 2 7 4	3 6 9 1 8
	5 4 1 8	3 7 9 2 6
	5 9 7 6	4 1 8 3 2
	7 6 1 4	5 3 2 9 8
8	3 1 8 7	2 5 4 9 6
	4 5 8 9	3 6 7 1 2
	4 5 9 1	3 6 7 2 8
	4 6 8 9	3 7 5 1 2
	4 6 9 1	3 7 5 2 8
	4 7 6 9	3 8 1 5 2
	5 2 3 7	4 1 8 9 6
	5 3 7 1	4 2 9 6 8
	5 7 8 9	4 6 3 1 2
	5 7 9 1	4 6 3 2 8
	5 8 3 9	4 6 7 1 2
	5 8 9 2	4 7 1 3 6
	5 9 1 6	4 7 3 2 8
	5 9 2 1	4 7 3 6 8
	6 4 7 9	5 1 8 3 2
	6 7 4 1	5 3 9 2 8
	6 7 8 9	5 4 3 1 2
	6 7 9 1	5 4 3 2 8
	6 8 3 9	5 4 7 1 2
	7 1 2 3	5 6 9 8 4
	7 3 1 2	5 8 4 9 6
	7 3 6 4	5 8 9 1 2
	7 4 1 6	5 9 3 2 8
	7 4 2 1	5 9 3 6 8
	7 8 9 4	6 3 1 5 2
	7 9 4 1	6 3 5 2 8
	8 1 7 4	6 5 3 9 2
	8 1 7 9	6 5 4 3 2
	8 3 9 4	6 7 1 5 2
	8 4 1 9	6 7 3 5 2
	8 4 3 9	6 7 5 1 2
	8 9 3 2	7 1 4 5 6
	8 9 4 2	7 1 5 3 6
	8 9 5 3	7 1 6 2 4
	8 9 5 4	7 1 6 3 2
	9 1 5 6	7 3 2 4 8
	9 1 5 8	7 3 2 6 4
	9 1 8 2	7 3 4 5 6
	9 3 1 6	7 4 5 2 8
	9 3 2 1	7 4 5 6 8
	9 3 5 2	7 4 8 1 6
	9 4 1 6	7 5 3 2 8
	9 4 2 1	7 5 3 6 8
	9 5 2 3	7 6 1 8 4
	9 5 3 1	7 6 2 4 8
	9 5 4 1	7 6 3 2 8
9	6 3 8 1	5 7 4 2 9
	6 4 7 1	5 8 2 3 9
	8 3 6 1	7 5 2 4 9

637.79000000000087

数列の規則を考えて、次の項を見つけてください。

１，１１，１２，１１２１，１２２１１１、・・・

ヒント：前の問題の応用です。　

正ｎ角形の各辺を２倍に延長した点を結んでできる正ｎ角形の面積が もとの何倍になっているかを考えます。

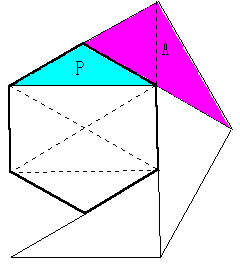例として，正６角形を考えると，もとの正６角形のまわりに赤い三角形Ｐを ６個くっつけた正６角形になります。
ここで，Ａ＝２Ｐとなるから，　面積は，もとの６角形より　１２Ｐ　増えます。
もとの正６角形の面積をＳとすると，Ｓ＝６Ｐであるから，（６Ｐ＋１２Ｐ）÷６Ｐ＝３倍になります。
（もっとも，この場合は，大きい正６角形の１辺が 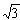倍になることは，簡単に示せますが。）

一般的に，正ｎ角形の場合もＡ＝２Ｐはなりたち，もとのｎ角形より，面積は　２ｎＰ　増える。
したがって，２辺で作られる水色の三角形Ｐと，もとの正ｎ角形の面積Ｓの比が求まれば計算できる。

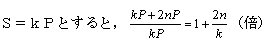
既知の三角形と，四角形で確認しておきます。
正３角形…ｋ＝１であるから，１＋２×３÷１＝７（倍）
正４角形…ｋ＝２であるから，１＋２×４÷２＝５（倍）
正６角形…ｋ＝６であるから，１＋２×６÷６＝３（倍）…（おまけ）

三角関数を使わずに求められそうな，正５角形と正８角形を求めておきます。

【正５角形】

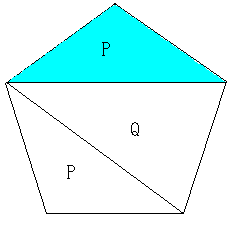１辺を１とすると対角線は 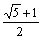であるから，
Ｑ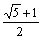＝ Ｐとなり，
Ｓ＝２Ｐ＋Ｑ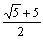＝ Ｐ
したがって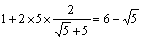， ＝3.7639…　（倍）

【正８角形】

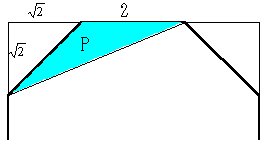１辺を２とすると，正８角形がちょうど収まる正方形の１辺は 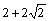, Ｐ＝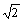
よって，Ｓ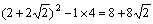＝ となり ｋ＝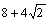
したがって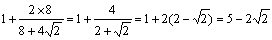， ＝2.17157…（倍）

【コメント】

ｎ→∞で１に収束しそうですが，するんでしょうか？
また，ちょうど２倍になる正ｎ角形は？

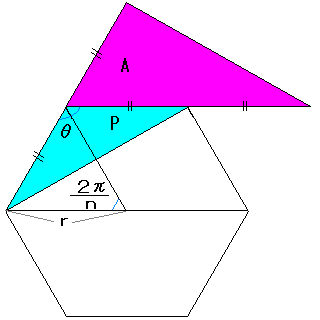
１辺の長さが１の正ｎ角形で考えます。(図は正６角形ですが・・・。)
右図の通り中心角が(２π/ｎ)なので、正ｎ角形の内角θは、θ＝２π−(２π/ｎ)　となります。

水色の部分Ｐの面積は、

Ｐ	＝(1/2)×１×１×sinθ
	＝(1/2)×sin{２π−(２π/ｎ)}
	＝(1/2)×sin(２π/ｎ)

一方、この正ｎ角形が外接する円の半径をｒとすると、正ｎ角形の面積Ｓは、
Ｓ＝(1/2)×ｒ×ｒ×sin(２π/ｎ)×ｎ

これより、Ｓ＝ｎｒ²Ｐという関係がでてきます。

NO.655で「sambaGREEN」さんが示してくださった、

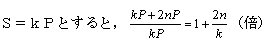
という式の　ｋ＝ｎｒ²ということになります。
さらに問題の倍率をＸ(ｎ)とすると、
Ｘ(ｎ)＝１＋(２ｎ／ｋ)＝１＋(２ｎ／ｎｒ²)＝１＋(２／ｒ²)・・・(1)となります。

さて、そろそろｒを追求しましょう。
正ｎ角形を中心角でｎ等分した三角形に対して、余弦定理を使います。

１2	＝ｒ2＋ｒ2−２ｒ×ｒ×cos(２π/ｎ)
	＝２ｒ2{１−cos(２π/ｎ)}

これから、(１／ｒ²)＝２{１−cos(２π/ｎ)}となります。 これを先程の(1)に代入します。

Ｘ(ｎ)	＝１＋(２／ｒ2)
	＝１＋４{１−cos(２π/ｎ)}
	＝５−４cos(２π/ｎ)　　→１（ｎ→∞）

というわけで「sambaGREEN」さんの予想通り１に収束するようです。

次にちょうど２倍となる正ｎ角形があるかどうか？　です。
Ｘ(ｎ)＝５−４cos(２π/ｎ)　＝２より、 cos(２π/ｎ)＝３／４　となりますが、これを満たすｎは存在しません。
従って、ちょうど２倍となる正ｎ角形はないという結論です。
ちなみに、mathematicaで計算してみると、２π/Arccos(3/4)＝8.69363･･･となりました。
正８角形で倍率Ｘ(８)＝２．１７１５７・・・、 正９角形で倍率Ｘ(９)＝１．９３５８２・・・でした。

第３５回数学的な応募問題

太郎さんは、「グレゴリオ暦」（西暦年号）を調べている中で、 歴史上の空白の１１日間があることに気が付きました。 ユルウス暦は１５８２年１０月４日（木曜日）までで、 明くる日はグレゴリオ暦の１５８２年１０月１５日（金曜日）になっています。 （ある本では１０月１２日の夜までと、朝起きて１０月２５日という出来事と書いてありました）
そこで、今回の問題です。西暦２０００年１月１日は土曜日です。

問題１：
西暦２１００年、西暦２２００年、西暦２３００年、西暦２４００年、 西暦２５００年の１月１日は何曜日ですか。

問題２：
西暦２０００年から４００年までの毎年の１月１日は何曜日になっているか、 その回数を求めてください。

問題３：
西暦の年数の下２桁が００である年（各世紀の最後の年）の１月１日は何曜日か 調べていくと、決して起こらない曜日があります。この曜日を求めてください。

＜参考文献＞：パズルより面白い中学入試の算数から一部改題（ピーター・フランクル）：講談社
太郎さんは、電算部にある万年カレンダーで調べてもらおうと思っています。

解答

２）	１	１が１回	−−＞	１１
３）	１１	１が２回	−−＞	１２
４）	１２	１が１回、２が１回	−−＞	１１２１
５）	１１２１	１が２回、２が１回、１が１回	−−＞	１２２１１１
６）	１２２１１１	１が１回、２が２回、１が３回	−−＞	１１２２１３
７）	１１２２１３	１が２回、２が２回、１が１回、３が１回	−−＞	１２２２１１３１

上記のような規則性がみられます。
答え　６）　１１２２１３

問題１：

３６５	＝７×５２＋１
	≡１　(MOD 7)

ですから、閏年でない年は１年で１日分、曜日がずれていきます。
さらに閏年はもう１日分、曜日がずれることになります。

• 西暦２１００年
  ２０００年〜２０９９年の間に閏年は２５回あります。 （２０００年が閏年であることに注意）
  

  １００＋２５	＝１２５
  	＝７×１７＋６
  	≡６　(MOD 7)

  
  従って、２１００年の１月１日は金曜日
  
  
• 西暦２２００年
  ２１００年〜２１９９年の間に閏年は２４回あります。
  

  ２００＋(２５＋２４)	＝２４９
  	＝７×３５＋４
  	≡４　(MOD 7)

  従って、２２００年の１月１日は水曜日
  
  
• 西暦２３００年
  ２２００年〜２２９９年の間に閏年は２４回あります。
  

  ３００＋(２５＋２４＋２４)	＝３７３
  	＝７×５３＋２
  	≡２　(MOD 7)

  従って、２３００年の１月１日は月曜日
  
  
• 西暦２４００年
  ２３００年〜２３９９年の間に閏年は２４回あります。
  

  ４００＋(２５＋２４＋２４＋２４)	＝４９７
  	＝７×７１
  	≡０　(MOD 7)

  従って、２４００年の１月１日は土曜日
  
  
• 西暦２５００年
  ４００年たったところでもとに戻っていることに気がつきます。
  従ってあとはこの繰り返しです。
  ２５００年の１月１日は２１００年の１月１日と同じで金曜日
  
  

問題２：

閏年でない年は１年で１日分、閏年は２日分、曜日がずれていきます。

４×７＝２８年たったところで元に戻りますが、 ２１００年、２２００年、２３００年は閏年にはならないので、 そこで微妙にずれてきます。
表にしてみました。

日	月	火	水	木	金	土	コメント
						2000	土曜日１回
	2001	2002	2003	2004		2005	２８年で１サイクル 各曜日４回ずつ
2006	2007	2008		2009	2010	2011
2012		2013	2014	2015	2016
2017	2018	2019	2020		2021	2022
2023	2024		2025	2026	2027	2028
・・・						2084	もう２サイクル,各曜日８回ずつ
	2085	2086	2087	2088		2089	日２回、月２回、火３回、水２回、木３回、金２回、土３回
2090	2091	2092		2093	2094	2095
2096		2097	2098	2099	2100	2101
2102	2103	2104		2105	2106	2107	８４年で３サイクル 各曜日１２回ずつ
・・・
2186	2187	2188		2189	2190	2191	日３回、月２回、火３回、水２回、木３回、金３回、土２回
2192		2193	2194	2195	2196
2197	2198	2199	2200	2201	2202	2203
2204		2205	2206	2207	2208		８４年で３サイクル 各曜日１２回ずつ
・・・
2288		2289	2290	2291	2292		日３回、月２回、火３回、水３回、木２回、金３回、土１回
2293	2294	2295	2296		2297	2298
2299	2300	2301	2302	2303	2304
2305	2306	2307	2308		2309	2310	８４年で３サイクル 各曜日１２回ずつ
・・・
2389	2390	2391	2392		2393	2394	日２回、月２回、火１回、水２回、木１回、金２回、土１回
2395	2396		2397	2398	2399	(2400)

３×４＝１２サイクルで４８回、それに半端分をたしていくと、
日５８回、月５６回、火５８回、水５７回、木５７回、金５８回、土５６回

問題３：

４００＋(２５＋２４＋２４＋２４)	＝４９７
	＝７×７１
	≡０　(MOD 7)

問題１のところで調べたように、 ４００年たったところでもとに戻っていることに気がつきます。
土曜日　−＞　金曜日　−＞　水曜日　−＞　月曜日　のサイクルが繰り返されるわけです。
言い換えれば、下２桁が「００」である年の１月１日は、決して日曜日、火曜日、木曜日 とはならないわけです。

第３６回数学的な応募問題

太郎さんの勤務している学校で、体育大会で「大縄跳び」競技があり、 こんな問題を考えました。

１直線上に２ｎ人の生徒が並んでいます。 大縄をｎ本渡して、２人で１組とし、 大縄が交差せずに競技ができるようにします。 このとき、生徒は区別しないで、ｎ本の大縄 の軌跡について、次の問に答えてください。

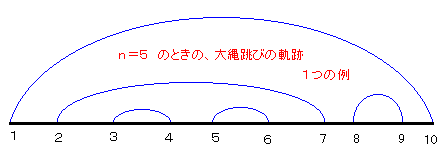
問題１：
ｎ＝１，ｎ＝２，ｎ＝３，ｎ＝４，のときの軌跡の数は何通りですか。

問題２：
一般の場合の軌跡の数を、ｎで表してください。

太郎さんは、過去に、このような数列を扱ったことを覚えています。

問題１：
ｎに対する軌跡の数をF(n)とすると、
n=1　　F(1)=1
n=2　　F(2)=2
n=3　　F(3)=5
n=4　　F(4)=14
これらは、図を描いて数えました。

問題２：

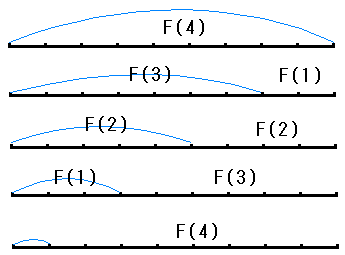
まず n=5の場合について考えてみました。(右図参照)
左から1,2,･･･,10と背番号をつけます。

• 1と10が縄をもつ場合
  その縄の中の人たちの縄の持ち方は、F(4)=14通りです。
  その縄の外には人がいません。
  
  
• 1と8が縄をもつ場合
  その縄の中の人たちの縄の持ち方は、F(3)=5通りです。
  その縄の外の人たちの縄の持ち方は、F(1)=1通りです。
  従って、F(3)×F(1)=5×1=5
  
  
• 1と6が縄をもつ場合
  その縄の中の人たちの縄の持ち方は、F(2)=2通りです。
  その縄の外の人たちの縄の持ち方は、F(2)=2通りです。
  従って、F(2)×F(2)=2×2=4
  
  
• 1と4が縄をもつ場合
  その縄の中の人たちの縄の持ち方は、F(1)=1通りです。
  その縄の外の人たちの縄の持ち方は、F(3)=5通りです。
  従って、F(1)×F(3)=1×5=5
  
  
• 1と2が縄をもつ場合
  その縄の中には人がいません。
  その縄の外の人たちの縄の持ち方は、F(4)=14通りです。
  
  

一般的にもこれと同じことが言えるはずですから、

F(n)=F(n-1)×F(0)+F(n-2)×F(1)+F(n-3)×F(2)+･･･+F(0)×F(n-1)

今朝、「宇宙開発事業団」 （ＮＡＳＤＡ)のＨ２ロケット打ち上げ失敗のニュースが話題になっています。
損失額は約３４３億円（ロケットは１５４億円）の膨大なものです。 そこで、問題です。

問１：
１０００個の部品で組み立てられているロケットがあります。
すべての部品の精度が０．９９９（スリー・ナイン）として、 １０００個の部品の中の少なくとも１つが故障して打つ上げに失敗する確率を求めなさい。

問２：
１万個の部品で組み立てられているロケットがあります。
すべての部品の精度が０．９９９（スリー・ナイン）として、 １万個の部品の中の少なくとも１つが故障して打つ上げに失敗する確率を求めなさい。

問３：
１０万個の部品で組み立てられているロケットがあります。
すべての部品の精度が０．９９９９９（ファイブ・ナイン）として、 １０万個の部品の中の少なくとも１つが故障して打つ上げに失敗する確率を求めなさい。

問４：
１０万個の部品で組み立てられているロケットがあります。
すべての部品の精度が０．９９９９９９（シックス・ナイン）として、 １０万個の部品の中の少なくとも１つが故障して打つ上げに失敗する確率を求めなさい。

問５：
１０万個の部品で組み立てられているロケットがあります。
すべての部品の精度が０．９９９９９９９（セブン・ナイン）として、 １０万個の部品の中の少なくとも１つが故障して打つ上げに失敗する確率を求めなさい。

皆さんは、どれだけの精度を高めたら、打ち上げをしますか、考えてください。

E-mail 戻る