
Weekend Mathematics/コロキウム室/1999.10〜12/NO.74
| NO.643 | '99 11/1 | kiyo | 数列の規則性(2) |
数列サイトで検索してみました。
1,2,2,1,1,2,1,2,2,1,2,2,1,1,2,1,1,2,2,1,2,1,1,2,1,2,2,1,1,2,
1,1,2,1,2,2,1,2,2,1,1,2,1,2,2,1,2,1,1,2,1,1,2,2,1,2,2,1,1,2,
1,2,2,1,2,2,1,1,2,1,1,2,1,2,2,1,2,1,1,2,2,1,2,2,1,1,2,1,2,2,
1,2,2,1,1,2,1,1,2,2,1,2,1,1,2,1,2,2
Name: Kolakoski sequence: a(n) is length of nth run.
M=50; a:=[1,2,2]; for n from 3 to M do for i from 1 to a[n] do a:
=[op(a),1+((n-1)mod 2)]; od: od: a;
Program: a=[1,2,2];for(n=3,80,for(i=1,a[n],a=concat(a,1+((n-1)%2)))); a
上記のようになっていました。

| NO.644 | '99 11/1 | 水の流れ | プレゼントの問題(16) |
皆さんは、プレゼントの問題(9)
の中にある次のような問題をご存じでしたか。
問題
A君は、あるテストの問題を考えています。
その問題は、5つの空欄のある文章の空欄に入る語句を5つの選択肢の中から選んで答える問題です。
問題には、同じ語句を二度以上用いてはならない、と書いてあるため、
5つの空欄には、全て異なる語句が入ることになります。
A君は、ちっとも勉強していなかったため、直感で答えを書くしかありませんが、
次の5つの方法のうち、どちらの書き方をした方が得でしょうか。

| NO.645 | '99 11/1 | junko | マセマティカル・ア−ト展 |

東海大学・建学祭(10/31〜11/3、湘南校舎)で
「マセマティカル・ア−ト展 」があるというので、でかけてみました。
秋山仁を中心に東海大学・教育開発研究所が独自に開発・制作した教材・教具が150点余り
展示されていました。
学生さんたちが親切に説明してくださる中、実際に触ったり動かしたりして実験してみることができます。
子供たちは夢中になって、いろいろなものに手を出していました。

「音楽を奏でる木」
1本1本の枝を木琴の鍵盤になぞらえ、それぞれの枝の長さを調節して木ができあがっています。
上から落下させた球が枝を叩くことによって美しいメロディを楽しむことができます。

「パチンコで数学」
等間隔に釘が打ってあるパチンコ台の中央上の部分からたくさんの球を落とします。
球は釘にぶつかるたびに左右いずれか一方に等確率で落ちます。
その結果、中央部が多く両端にいくほど少なくなる山形になります。
これがいわゆる二項分布というものです。

「どの滑り台が一番早いか?」
奥から、直線、円弧、サイクロイド、円弧の4種類の滑り台があります。
各滑り台の最高地点からボ−ルを転がすと、どのボ−ルがより早く地面に到達するでしょうか?
実際に実験してみるとわかります。
サイクロイド曲線に沿って落ちるピンクのボ−ルが一番早く地面に到達します。
これが最速降下問題と呼ばれるものです。
これらの教材を見てみたい! と言う方にうれしいお知らせです。
国立科学博物館において、
「数学と遊ぼう かたちと数のワンダーランド」という催しが開かれます。
いくつかの教材はこちらにも出品されるようですし、
開催期間が長いので機会を見つけて出かけてみてはいかがでしょう?
開催期間/ 1999年11月16日(火)〜2000年1月16日(日)
月曜日・年末年始(12月28日〜1月4日)休館
ただし1月10日開館、11日休館
開館時間/ 9:00〜16:30 (入館は16:00まで)
入館料/ 通常料金(一般・大学生 420円、小・中・高校生 70円
お問い合わせ/ NTT東日本ハローダイヤル 03-3272-8600

| NO.646 | '99 11/1 | junko | 三角形の問題・その後(1) |
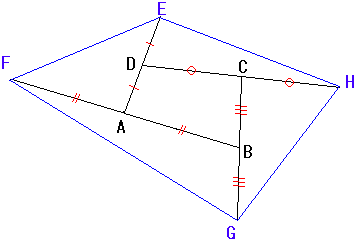
三角形の問題の発展問題です。
三角形ではなく四角形ではどうでしょう?
つまり左の図のように、四角形ABCDの各辺をそれぞれ1方方向に2倍に延長して
四角形EFGHを作ります。
この時、四角形EFGHの面積は、もとの四角形ABCDの面積の何倍になるでしょうか?
出典:「パズルよりおもしろい中学入試の算数」

| NO.647 | '99 11/1 | 水の流れ | 数列の規則性(3) |
| 1, | 2,2, | 1,1, | 2, | 1, | 2,2, | 1, | 2,2, | 1,1, | 2, | ・・・・ |
| 1, | 2, | 2, | 1, | 1, | 2, | 1, | 2, | 2, | 1, | ・・・ |
この数列は、1と2とは連続して何個あるかに注目すると分かってきます。
下の数列は上の数列と同じになるように出てくるのです。
また、この数列には周期性がないそうです。
さらに、一般項はまだ、分かっていないのです。
誰かさらに深く研究すると、意外なことが分かるかも。

| NO.648 | '99 11/1 | 水の流れ | 五輪の和(1) |
太郎さんは、来年のシドニーで行われるオリンピックの旗をみて次のような問題を考えました。
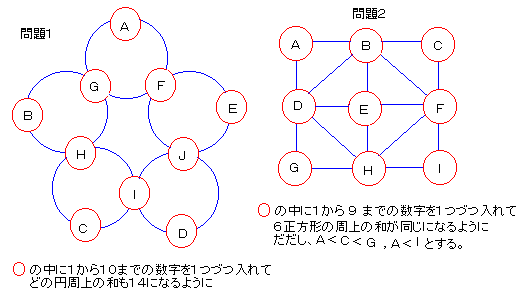
問題1:
「下図の○の中に1から10までの数字を1つずつ入れて、
どの円周上の数字の和も14になるように入れてください。」
ただし、A<B<C<D<E とする。
問題2:
「下図の○の中に1から9までの数字を1つずつ入れて、
6つの正方形の周上の数字の和が同じになるように、入れてください。」
ただし、A<C<G、A<I とする。
<出典問題1>:数とその歴史53話の中にあるトライ問題(上垣渉 何森仁 共著):三省堂
<出典問題2>:パズル数学入門(田村三郎 藤村幸三郎共著):講談社
太郎さんは、数字の入れ方を実際知りません。
生徒に入れてもらって、考えようと思っています。

| NO.649 | '99 11/1 | kiyo | 五輪の和(2) |
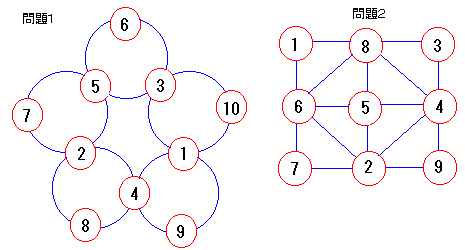
問題1
A=6, B=7, C=8, D=9 ,E=10, F=3, G=5, H=2, I=4, J=1
問題2
和 20
1+8+6+5=20
8+3+5+4=20
6+5+7+2=20
5+4+2+9=20
8+6+4+2=20
1+3+7+9=20

| NO.650 | '99 11/2 | junko | 五輪の和(3) |

問題1
5つの輪をすべて足します。
(A+B+C+D+E)+2×(F+G+H+I+J)=14×5=70
一方、A+B+C+D+E+F+G+H+I+J=1+2+3+4+5+6+7+8+9+10=55
この2式の差をとることにより、F+G+H+I+J=15
これは、{F,G,H,I,J}={1,2,3,4,5}しかありません。
従って、{A,B,C,D,E}={6,7,8,9,10}
A<B<C<D<E より、A=6, B=7, C=8, D=9 ,E=10 が決定。
F+J=4で同じ数字は入らないので、{F,J}={1,3}
F=1,J=3と埋めていくと矛盾を生じます。
F=3,J=1と埋めていくとうまく入ります。
その結果、F=3, G=5, H=2, I=4, J=1
問題2
正方形の数字の和をXとする。
A+B+D+E=X,B+C+E+F=X,D+E+G+H=X,E+F+H+I=X,A+C+G+I=X,B+D+H+F=X
(A+B+D+E)+(B+C+E+F)+(D+E+G+H)+(E+F+H+I)-(A+C+G+I)-2×(B+D+H+F)=4E
つまり、X=4E ・・・(1)
A+B+C+D+E+F+G+H+I=1+2+3+・・・+8+9=45
(A+C+G+I)+(B+D+H+F)+E=45
2X+E=45 ・・・(2)
(1),(2)より、E=5、X=20
条件にある大小関係を考えなければ、対称性から 1の入る場所は B か A のどちらかです。
もし、B=1 とすると B+E=6 ですから、A+D=14,C+F=14となります。
異なる数で和が14になるものは6+8=1しかありません(5+9=14は使えません)のでこれはだめです。
従って大小関係もかんがみて、A=1であることがわかります。
D+B=14 より、{D,B}={6,8}
H+F=6 より、{H,F}={2,4}
これより、I=9
残りの{G,C}={3,7}ですが、C<Gより、C=3,G=7
B+F=12,D+H=8 などから、B=8,D=6,H=2,F=4

| NO.651 | '99 11/3 | sambaGREEN | 三角形の問題・その後(2) |

各辺をn倍に延長した四角形の場合を考えます。
△GHC=n・△BHC=n・(n−1)△BCD
△AEF=n・△ADF=n・(n−1)△BADとなり,
△GHC+△AEF=n(n−1)(△BCD+△BAD)=n(n−1)・四角形ABCD
対称性から
△HED+△FGB=n(n−1)・四角形ABCDとなるから,
2n(n−1)+1=2n2−2n+1 (倍)
問題の図の場合は n=2 を代入して 5倍

| NO.652 | '99 11/3 | 水の流れ | 約分(1) |
太郎さんは、生徒が数学を楽しく学ぶためには「数覚」を磨く必要があると常に思っています。
その中に、数がどんな素数から成り立っているかを見分ける能力があります。
いわゆる素因数分解です。
ときどき、授業中、1から100までの合成数の分解や素数を早く発見する
「数覚」を鍛錬しています。
そこで、今回の問題です。
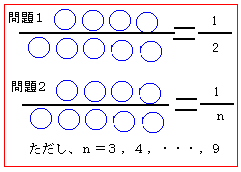
問題1:
「左図の○の中に1から9までの数字を1つずつ用いて、
分母が5桁、分子が4桁の分数を作る。
この分数を約分することによって、1/2となるようにしてください。」
問題2:
「左図の○の中に1から9までの数字を1つずつ用いて、
分母が5桁、分子が4桁の分数を作る。
この分数を約分することによって、1/3、1/4,…、1/9と
なるようにしてください。」
<出典問題>:数とその歴史53話の中にあるトライ問題(上垣渉 何森仁 共著):三省堂
太郎さんは、数字の入れ方を実際知りません。
生徒に入れてもらって、考えようと思っています。

 E-mail
E-mail
 戻る
戻る