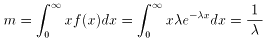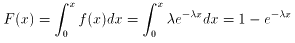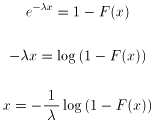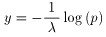指数分布 f(x)=λeーλx (x>0)について考えます。
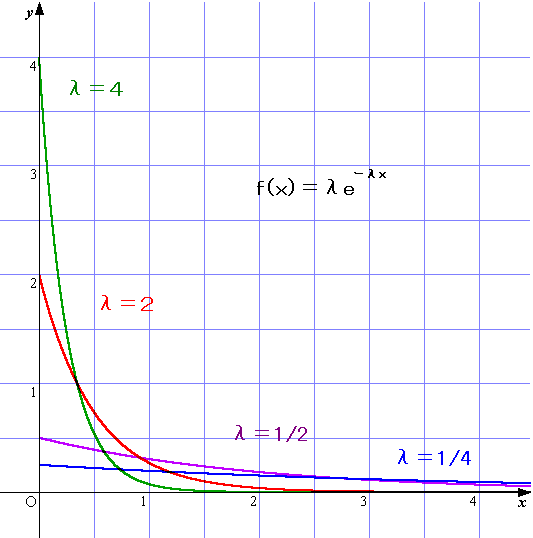
y=f(x)のグラフは以下のようになります。(λ=1/4,1/2,2,4)
平均値は、部分積分により、以下のようになります。
この分布の特徴は、ほとんどが平均のあたりに分布するものの、 ごくまれに大きな値が発生するということです。
待ち行列を考える際の到着間隔は、この分布で近似することができます。
指数分布になるような、乱数(指数乱数)を発生させるにはどうしたらよいでしょうか?
まずは累積確率関数F(x)を求めることにします。
これの逆関数を求めます。
ここでF(x)に一様乱数を与えればいいわけですが、 F(x)が一様乱数ならば1−F(x)も一様乱数ですから、簡単にpと書くことにすれば、
となります。1/λは元の指数分布の平均ですから、 例えば平均4の指数分布をするような乱数を得たいのであるならば、
y=ー4log(p)
としてやればいいわけです。