
Weekend Mathematics乛僐儘僉僂儉幒乛僥乕儅暿乛40.惓嶰妏宍偺撪晹傪摦偔慄暘
| NO.1066 | 2001.10.17. | yokodon | 惓嶰妏宍偺撪晹傪摦偔慄暘乮侾乯 |
a 偼 併3亙 a 亙 2 傪枮偨偡掕悢偲偡傞丅
堦曈偺挿偝偑俀偺惓嶰妏宍俙俛俠偺曈俙俛丄曈俙俠忋乮扐偟丄抂揰傪彍偔乯偵偦傟
偧傟揰俹丄揰俻偑偁傝丄俹俻亖 a 傪枮偨偟側偑傜摦偔傕偺偲偡傞丅
嶰妏宍俙俹俻偺柺愊偺庢傝偆傞抣偺斖埻傪丄a 傪梡偄偰昞偣丅

| NO.1067 | 2001.10.18. | BossF | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俀乯 |
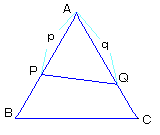
AP=p , AQ=q 偲偍偔丄
傑偢梋尫掕棟傛傝丂
a2=p2+q2-2pq丒cos60亱=p2+q2-pq
亪(p-q)2+pq=a2, i.e. pq=a2-(p-q)2
偟偨偑偭偰丂pq亝a2
傑偨丂p or q 仺0 偱丂pq仺0 偼偁偒傜偐
傛偭偰丂0亙pq亝a2
偝偰
仮APQ=pq丒sin60亱x1/2=乮併3/4乯pq偩偐傜
仮APQ亝乮併3/4乯a2 (摍崋偼AP=AQ偺帪)乧摎

| NO.1071 | 2001.10.22. | 昹揷丂柧枻 | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俁乯 |
俙俹亖倶丆俙俻亖倷偲偡傞丏
仮俙俹俻偵偍偄偰丆梋尫掕棟偐傜丆
俹俻2亖俙俹2亄俙俻2亅俀丒俙俹丒俙俻丒cos佢俹俙俻
亪倎2亖倶2亄倷2亅倶倷乧乧乧(1)
偙偺曽掱幃偱昞偝傟傞僌儔僼傪丆尨揰傪拞怱偵偟偰兤夞揮偝偣傞丏
偙偺夞揮傪昞偡幃偼丆
丂丂倶'亖倶cos兤亅倷sin兤丆倷'亖倶sin兤亄倷cos兤
偱偁傞偐傜丆
丂丂倶亖倶'cos兤亄倷'sin兤丆倷亖亅倶'sin兤亄倷'cos兤
偲側傞丏
(1)偵戙擖偡傞偲丆
丂丂倎2亖(倶'cos兤亄倷'sin兤)2亄(亅倶'sin兤亄倷'cos兤)2亅(倶'cos兤亄倷'sin兤)(亅倶'sin兤亄倷'cos兤)
丂丂亪倶'2(侾亄sin俀兤乛俀)亄倷'2(侾亅sin俀兤乛俀)亅倶'倷'cos俀兤亖倎2
cos俀兤亖侽偲偡傞堊偵偼丆兤亖兾乛係偲偡傟偽傛偄丏
偙偺偲偒丆
丂丂俁倶'2乛俀亄倷'2乛俀亖倎2
丂丂亪倶'2乛(俀倎2乛俁)亄倷'2乛(俀倎2)亖侾
丂(倶'丆倷')傪(倶丆倷)偵偐偊傞偲丆
丂丂倶2乛(俀倎2乛俁)亄倷2乛(俀倎2)亖侾乧乧乧(2)
偙傟傪昞偡僌儔僼偼恾侾偱偁傞丏
恾侾
偮傑傝(1)偺昞偡僌儔僼偼丆恾侾偺僌儔僼傪尨揰傪拞怱偵偟偰亅兾乛係夞揮偟偨傕偺偺丆
倶亜侽丆倷亜侽偺晹暘偱偁傞丏偮傑傝恾俀偲側傞丏
恾俀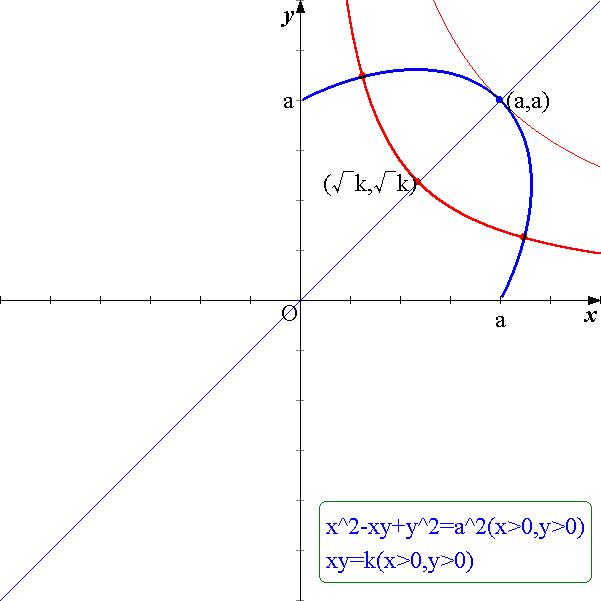
偙偙偱丆
仮俙俹俻亖侾乛俀丒俙俹丒俙俻丒sin佢俹俙俻亖併俁乛係丒倶倷
偮傑傝倶倷偺抣偺併俁乛係攞偑仮俙俹俻偺柺愊偱偁傞偺偱丆倶倷偺抣偺斖埻傪媮傔傟偽傛偄丏
倶倷亖倠乮亜侽乯偲偡傞偲丆偙傟偼倶幉丆倷幉傪慟嬤慄偲偡傞捈妏憃嬋慄偱偁傞丏
恾俀偐傜丆倶倷亖倠偑嵟戝偲側傞偺偼丆偙偺憃嬋慄偑揰(倎丆倎)傪捠傞乮愙偡傞乯偲偒偱偁傞偺偱丆
偙偺偲偒丆
丂丂倠亖倎2
偮傑傝丆倠偺抣偺斖埻偼丆
丂丂侽亙倠亝倎2
偱偁傞偺偱丆媮傔傞摎偼丆
丂丂侽亙仮俙俹俻亝併俁乛係丒倎2
偱偁傞丏

| NO.1073 | 2001.10.24. | yokodon | 惓嶰妏宍偺撪晹傪摦偔慄暘乮係乯 |
No.1067 偺夝摎偱偡偑丄
梋尫掕棟偐傜 p , q 偺忦審幃傪弌偡偲偙傠傑偱偼椙偄偺偱偡偑丄栤戣偼偦偺屻偱偡丅
偙偙偱偼娙扨偺偨傔丄揰俹丄俻偑曈偺椉抂傕娷傔偰摦偔傕偺偲偟傑偟傚偆乮戣堄偲
偼堘偄傑偡偑乯丅
偙偺傕偲偱丄p, q 偼嫟偵 0 亝 p,q 亝 2 偺斖埻傪摦偒傑偡偑丄0 偲 2 偺偁偄偩
偺慡偰偺幚悢傪偲傟傞偐偳偆偐偼帺柧偱偼偁傝傑偣傫丅
幚嵺丄杮栤偺応崌丄併3 亙 a亙 2 偺壖掕偑偁傞偺偱丄
p , q 偼 0 亝 p,q 亝 2 偺斖埻傪楢懕偵摦偗傑偣傫丅
偙偺偙偲傪丄恾偱峫偊偰傒傑偟傚偆丅
峫偊摼傞忬嫷偼丄埲壓偺俁偮偱偡丅
乮i乯 0 亝 p,q 亝 1
乮ii乯 0 亝 p 亝 1 亙 q 亝 2 丄枖偼 0 亝 q 亝 1 亙 p 亝 2
乮iii乯 1 亙 p,q 亝 2
乮i乯偺応崌偼丄a 偺忦審偐傜晄壜擻偱偡丅
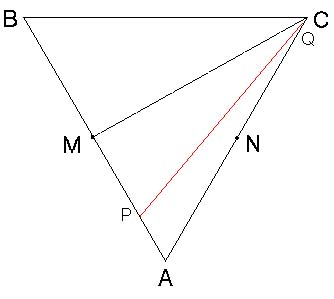
乮ii乯偺擇偮偺応崌偼丄曈俛俠偺拞慄偵娭偟偰懳徧堏摦偡傟偽杮幙揑偵摨偠忬嫷傪
昞偡偺偱丄慜幰偱峫偊傑偡丅
嶰妏宍俙俛俠偺曈俙俛丄曈俙俠偺拞揰傪偦傟偧傟俵丄俶偲偟傑偡丅偙偺偲偒丄揰俹
偼慄暘俙俵忋丄揰俻偼慄暘俶俠忋偵偁傝傑偡丅揰俹偑揰俙偲堦抳偡傞偲偒丄俠俻亖2
- a 偱偡偹丅偙偙偱丄揰俹傪揰俛偺曽岦偵摦偐偟偰傒傞偲丄揰俙偑揰俵偵帄傜側偄偆
偪偵丄揰俻偼揰俠偵摓拝偟偰偟傑偄丄偦偙偱慄暘俹俻偼偮偭偐偊偰偟傑偄傑偡丅
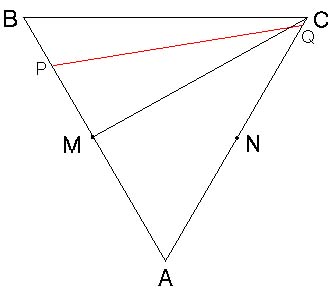
乮iii乯偺応崌偼丄乧僐儗偑嵟傕巚偄偮偒傗偡偄偲巚傢傟傑偡偑乧丄摉弶揰俹偑揰
俛偵堦抳偟偰偄偨偲偒丄揰俻偼慄暘俠俻忋偵偁傝傑偡偹丅偦偙偐傜揰俹傪揰俙偺曽岦
偵摦偐偡偲丄偁傞偲偙傠偱慄暘俹俻偼曈俛俠偵暯峴偵側傝傑偡丅偦偙偐傜峏偵摦偐偡
偲丄偁傞偲偙傠傑偱揰俹偑棃偨偲偒偵丄揰俻偼揰俠偵堦抳偟偰偟傑偄丄偦偙偱偮偭偐
偊偰偟傑偄傑偡丅
椺偊偽丄a 亖 11/6 摍偲偟偰丄幚嵺偵幚尡側偝偭偰傒傞偲丄忬嫷偑暘偐傝傗偡偄偲
巚偄傑偡丅

| NO.1074 | 2001.10.25. | 昹揷丂柧枻 | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俆乯 |
寁嶼偵傛傞摎偑弌偦傠偭偨偲偙傠側偺偱乮偄偮偺榖丠乯丆
偙偙偱僷僜僐儞偺僾儘僌儔儉偵傛傞夝摎傪搳峞偟傑偡丏
崱夞偼俧俼俙俹俤俽傪棙梡偟偰夝偄偰傒傑偟偨丏
俙(侾丆併俁)丆俛(侽丆侽)丆俠(俀丆侽)丆俙俹亖倫丆俙俻亖倯丆
捈慄俙俛丗倷亖倖(倶)丆捈慄俙俠丗倷亖倗(倶)
偲偡傞偲丆
倖(倶)亖併俁倶丆倗(倶)亖亅併俁(倶亅俙倶)亄俙倷丆
俹(侾亅倫乛俀丆倖(俹倶))丆俻(侾亅倯乛俀丆倗(俻倶))丆
傑偨倫2亄倯2亅倫倯亖倎2丆倫亜侽丆倯亜侽偱偁傞偐傜丆
倯亖(倯亄併(係倎2亅俁倫2))乛俀
偲側傞丏
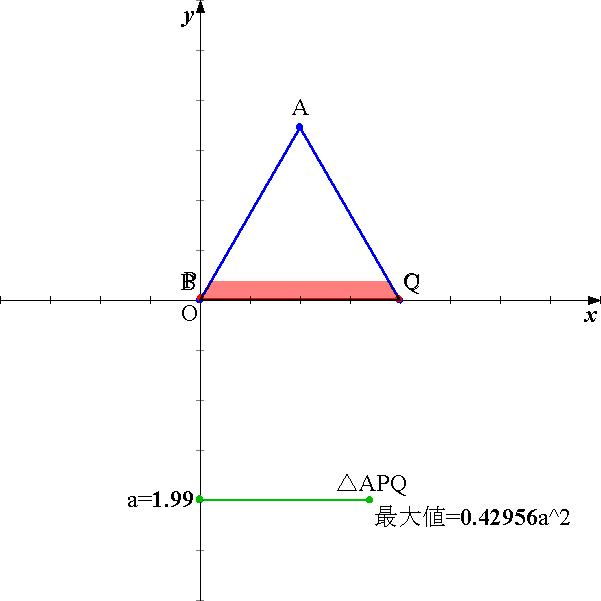
丂偙傟傜偺偙偲偑傜偐傜丆師偺俧俼俙俹俤俽偺僗僋儕僾僩傪嶌惉偟偰傒偨丏
# file://Click偱寁嶼奐巒 # clraimg # k:=.01 # for a:=Sqrt(3)+k to 2-k step k # t:=0 # for p:=k to 2-k step k # m:=Ax-p*.5 # q:=(p+Sqrt(4*a*a-3*p*p))*.5 # n:=Ax+q*.5 # if n<2 then # s:=.5*p*q*sin(Pi/3) # if t< s then # t:=s # u:=m # v:=n # endif # draw # endif # next # c:=u # d:=v # draw # next # ---

| NO.1075 | 2001.10.25. | BossF | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俇乯 |
乮^^丟丟Yokodon偝傫偺偍偭偟傖傞捠傝乧
乽傑偨丂p or q 仺0 偱丂pq仺0 偼偁偒傜偐乿偼堘偭偰傑偡偹丄埲壓掶惓
乽AP=p , AQ=q 偲偍偔丄
傑偢梋尫掕棟傛傝丂
a2=p2+q2-2pq丒cos60亱=p2+q2-pq
亪(p-q)2+pq=a2, i.e. pq=a2-(p-q)2乧嘆
偟偨偑偭偰丂pq亝a2
偙偙偱丄pq偺嵟彫抣傪峫偊傞丅
傑偢丄p亙q偲偟偰傕堦斒惈傪幐傢偢
嘆傛傝d=q-p偑嵟戝偺帪偵pq偼嵟彫偱偁傞偙偲偵拲堄偡傞丅
i) a亝併3偺偲偒
p偑梌偊傜傟傞偲堦斒偵q偼擇捠傝偁傞偑丄偦偺戝偒偄曽偺q傪峫偊傞丅
偁偒傜偐偵 p 仺0 偑壜擻偱丄偦偺偲偒 d仺Max
丂丂丂丂丂丂丂丂丂丂丂丂丂傛偭偰嵟彫抣側偟
ii)a亜併3 偺偲偒
q偑梌偊傜傟傞偲堦斒偵p偼擇捠傝偁傞偑丄偦偺彫偝偄曽偺q傪峫偊傞丅
偁偒傜偐偵 q 仺2 偑壜擻偱丄偦偺偲偒 d仺Max
丂丂丂丂丂丂丂丂丂丂丂丂丂傛偭偰嵟彫抣側偟
埲忋傛傝丂pq亝a2
偝偰
仮APQ=pq丒sin60亱x1/2=乮併3/4乯pq偩偐傜
仮APQ亝乮併3/4乯a2 (摍崋偼AP=AQ偺帪)乧摎乿

| NO.1076 | 2001.10.28. | 昹揷丂柧枻 | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俈乯 |
忦審偐傜丆
丂丂倶2亄倷2亅倶倷亖倎2乧乧乧(1)
丂丂侽亙倶亙俀丆侽亙倷亙俀丆併俁亙倎亙俀乧乧乧(2)
偵偍偄偰
丂丂倶倷亖倠
偺抣偺斖埻傪媮傔傟偽傛偄偙偲偑暘偐傞丏
丂倶丆倷偺懳徧惈偐傜丆倷亞倶偺斖埻偱峫偊傟偽傛偄丏
丂(1)偵偍偄偰丆倷亖俀偲偡傞偲丆
丂丂倶2亄係亅俀倶亖倎2
丂丂亪倶2亅俀倶亄係亅倎2亖侽
丂丂亪倶亖侾亇併(倎2亅俁)
丂丂丂丂丂丂丂丂丂丂乮塭偺惡丗偩偐傜倎亜併俁側傫偩両乯
丂偮傑傝捈慄倷亖俀偲嬋慄(1)偺岎揰偺嵗昗偼丆
丂丂(侾亇併(倎2亅俁)丆俀)
偱偁傞丏
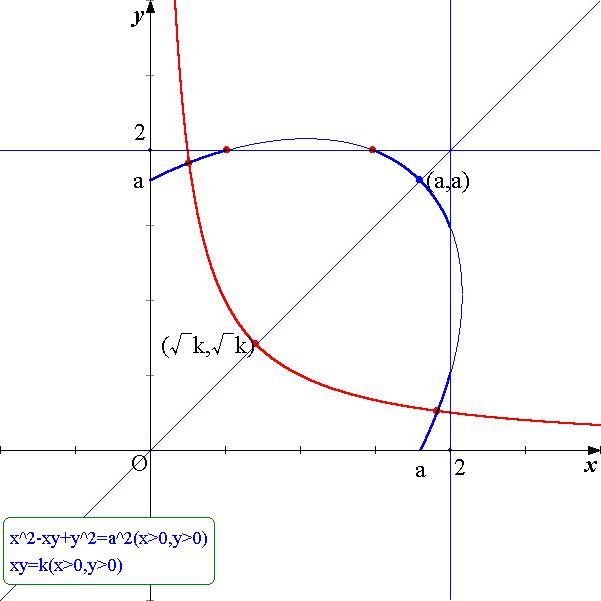
丂僌儔僼偐傜
丂丂侾亅併(倎2亅俁)亝倶亝侾亄併(倎2亅俁)
偺斖埻偱偼丆倷亞俀偲側傝丆倷偼懚嵼偟側偄偙偲偑暘偐傞丏
丂屘偵倶倷偼丆
丂丂俀{侾亅併(倎2亅俁)}偐傜俀{侾亄併(倎2亅俁)}傑偱
偺斖埻偺抣傪偲傜側偄丏
丂僌儔僼偐傜丆
丂丂侽亙倶倷亙俀{侾亅併(倎2亅俁)}丆俀{侾亄併(倎2亅俁)}亙倶倷亝倎2
丂仮俙俹俻亖併俁乛係丒倶倷偱偁傞偐傜丆
丂丂侽亙仮俙俹俻亙併俁乛俀丒{侾亅併(倎2亅俁)}丆
丂丂併俁乛俀丒{侾亄併(倎2亅俁)}亙仮俙俹俻亝併俁乛係丒倎2

| NO.1078 | 2001.11.2. | yokodon | 惓嶰妏宍偺撪晹傪摦偔慄暘乮俉乯 |
No.1076 偺昹揷偝傫偺偍摎偊偱惓夝偱偡乮(^恖^)丂僷僠僷僠乯丅
偙偙偱偼丄梋尫掕棟偐傜摼偨忦審幃偺懳徧惈傪妶梡偟偨暿夝傪偛徯夘偟偨偄偲巚偄傑偡丅
側偍丄俙俹亖 p 丄俙俻亖 q 偲偝偣偰壓偝偄丅
傑偢丄
a2 亖 p2 + q2 - pq 丂乧[1]
偱偡偹丅
p , q 偼丄偄偢傟傕侽偲俀偺偁偄偩傪摦偔偺偱丄
u 亖 p + q 丄v 亖 pq
偲偍偔偲丄p,q 偼埲壓偺俀師曽掱幃偺侽乣俀偺偁偄偩偺幚悢夝乮廳夝傪娷傓乯偲側傝
傑偡丅
t2 - ut - v 亖 0
偙偺嵍曈傪 f(t) 偲偍偄偰丄偦偺傛偆側 p,q 偑懚嵼偡傞偨傔偺忦審偼丄
f(0) 亜 0 丄f(2) 亜 0 丄0 亙乮幉乯亙 2 丄乮敾暿幃乯亞 0
偱偡丅偙傟傪丄u 媦傃 v 偺幃偵捈偡偲丄埲壓偱偡丅
v 亜 0 丄4 - 2u + v 亜 0 丄0 亙 u/2 亙 2 丄u2 - 4v 亞 0 丂乧[2]
[1]幃傪 u , v 偺幃偵彂偒捈偡偲丄埲壓偱偡丅
a2 亖 u2 - 3v丂丂乧[3]
[2] 偍傛傃 [3] 偺椉幃偐傜丄傑偢 u 偺抣堟傪媮傔傑偡丅
椉幃偐傜 v 傪徚嫀偟丄
a 亙 3 - 併(a2-3) 亙 3 + 併(a2-3) 亙 2a 亙 4
偵拲堄偟偰惍棟偡傞偲丄偦偺抣堟偼埲壓偱偡丅
a 亙 u 亙 3 - 併(a2-3) 丄 3 + 併(a2-3) 亙 u 亝 2a 丂乧[4]
偙偺 [4] 偺傕偲偱 u 偺娭悢 v 乮 v 亖 1/3丒(u2 - a2) 乯偺庢傝偆傞抣堟偼丄
偙偺椉嬫娫偱 v 偑 u 偺娭悢偲偟偰扨挷憹壛偱偁傞偙偲偵拲堄偟偰丄
0 亙 v 亙 2丒{1 - 併(a2-3) 丄
2丒{1 + 併(a2-3)} 亙 v 亝 a2
偲側傝傑偡丅
嶰妏宍俙俹俻偺柺愊傪俽偲偡傞偲丄俽亖併3/4丒v 偱偡偐傜丄嵟廔揑偵埲壓偺寢壥
傪摼傑偡丅
0 亙 S 亙 併3/2丒{1 - 併(a2-3)} 丄
併3/2丒{1 + 併(a2-3)} 亙 S 亝 併3/4丒a2
埲慜偺 No.1020 亀摦偔惓嶰妏宍亁偲摨條丄
懳徧惈偵拝栚偡傞偲婎杮懳徧幃偺妶梡
偱夝寛偱偒傞乮cf. No.1037乯偲偄偆栤戣偱偟偨丅

 栠傞
栠傞