Weekend Mathematics/コロキウム室/テーマ別
/18.不思議な級数
NO.386 '99 3/6 月の光 不思議な級数(1)
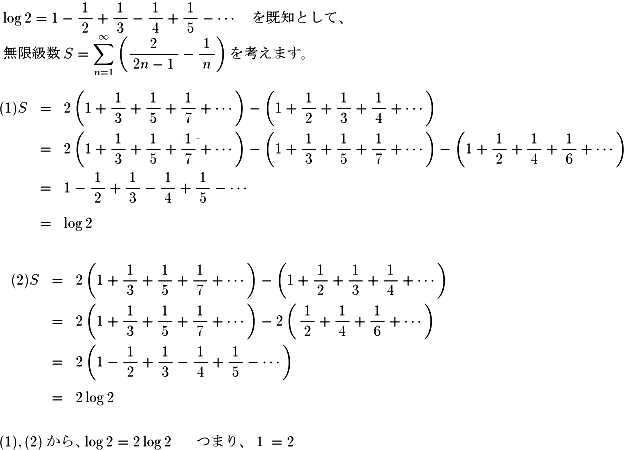
どうでしょうか? 実はこれには種も仕掛もあります。
それでもこの結果が出たときは驚きました。

NO.389 '99 3/8 Idaho Potato 不思議な級数(2)
No.386の月の光さんの問題とよく似た話で、 私が知っているのは、
に対するエレガントな証明(?)です。
もちろん、月の光さんもおっしゃるように、 これには種も仕掛けもあります。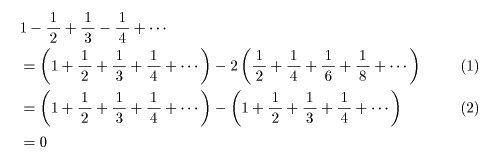
(1) すべてのマイナスの項をいったんプラスに変えて、 あとからマイナスの項を2倍して引く。
(2) ( ) の前の係数 2 を展開する。

NO.417 '99 3/23 Junko 不思議な級数(3)
有限なものについては、交換法則、結合法則が成り立ちますが、
無限級数を扱う際には足していく順序を変えたり、
変則的な足し方をするのは危険だということですね。
NO.386とNO.389の
両方にでてくる、調和級数1+1/2+1/3+1/4+・・・は無限大に発散することが
わかっています。
(NO.343、NO.346、
NO.357など)
収束しないものを足したり、ひいたりすることはできません。
特に、NO.389の式(2)は
「+∽−∽」となっていていわゆる不定形ですから「=0」はまずいわけです。


NO.455 '99 5/1 Junko 不思議な級数(4)
かの名著高木貞治の「解析概論」の中に、
これに関する記述がありましたので抜粋してここにまとめてみます。
無限級数Σanに対して、Σ|an|が収束するとき、
級数Σanは絶対収束するといいます。
級数Σanが絶対収束するならば、
もとの級数Σanも収束します。
Σanにおいて、正項をp1、p2、・・・、
負項を−q1、−q2、・・・とかき、
p=Σpn、q=Σqnとします。
p、qが共に有限(≠∽)のときは、
Σ|an|=p+qで絶対収束をしますからΣanも収束し、
Σan=p−qとなります。
級数Σanが収束するけれども、絶対収束はしないというとき、
これを条件収束するといいます。
p、qの一方だけが∽のときは、Σanが収束しないことになりますから、
条件収束のときは、p、q共に∽ということになります。
これについては、
条件収束する級数は、項の順序を適当に変更して任意の和に収束させたり、 また収束性を失わせたりすることができる。と、Dirichlet(1829)が指摘したということです。
たとえば、Σanの項の順序を入れ替えて任意の正数cに収束させるのは
どうするか?
正項p1、p2、・・・を順に加えて、
pαで初めてcより大きくなったとする。
次に負項−q1、−q2、・・・を順に加えて、
−qβで初めてcより小さくなったとする。
次にまた正項pα+1、pα+2、・・・を順に加えて、
pα+γで初めてcより大きくなったとする。
以下同様の作業を繰り返す。
(p1+p2+・・・+pα)−
(q1+q2+・・・+qβ)+
(pα+1+pα+2+・・・+pα+γ)−・・・
p=Σpn=∽、q=Σqn=∽ですから、
必ずcを越えることは保証されています。
またcを中心とした振れ幅は次第に小さくなり、いずれcに収束していくわけです。
具体的な例が載っています。

(詳しくは「解析概論」 p.153)

 戻る
戻る