数学アレルギーの友達にこの問題をやらせてみると、
4/5=1/5+ 1/5+1/5 +1/5 と、答えました。
確かにそうですね。他にも同じ事を考えた人がいるのではないでしょうか。

Weekend Mathematics/コロキウム室/テーマ別
/12.分数の問題その後
NO.250 '99 1/1 月の光 分数の問題・その後(1) 数学アレルギーの友達にこの問題をやらせてみると、
4/5=1/5+ 1/5+1/5 +1/5 と、答えました。
確かにそうですね。他にも同じ事を考えた人がいるのではないでしょうか。


NO.251 '99 1/1 Junko 分数の問題・その後(2) これはすごいですね。検証してみました。
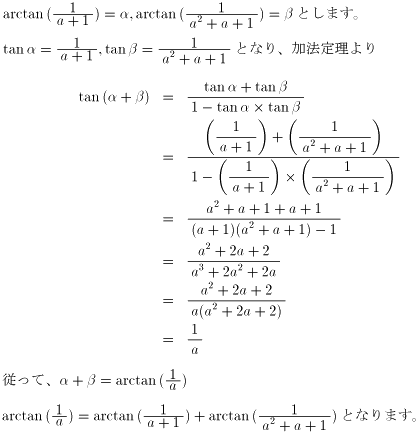
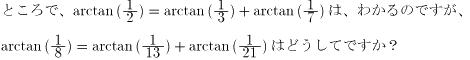

NO.253 '99 1/1 月の光 分数の問題・その後(3)



NO.254 '99 1/3 Idaho Potato 分数の問題・その後(4) 定理:任意の分数(正確に言うと正の有理数)は
必ず異なる単位分数の和として表すことができる 補題1:与えられた分数を超えない単位分数の中で一番大きいものを
引いていきます。これを何回か繰り返すと、必ず残りも単位分数になります。 補題1の証明に含まれている仮定のうち、
「b<a」は証明の中で使われていないので、
補題1自体は、与えられた分数が1以上であっても成り立ちます。 定理の正しい証明を与えるには、次のように議論を修正すればOKです。 次の有名な事実を使います。 命題:調和級数 1 + 1/2 + 1/3 + ... は、正の無限大に発散する。 補題2:任意の正の実数 x について、 さて、与えられた正の有理数を x とします。
を証明するのに、
を証明して、その系として定理が得られる、としていますが、
実はそれでは不十分であることに気づきました。
また、与えられた分数が2未満の場合には、
同じ単位分数が高々1度しか使われないことは、容易にわかります。
しかし、与えられた分数が2以上の場合は、
補題1によって与えられるアルゴリズムで単位分数に分解しようとすると、
1を複数回使うことになってしまいます。
これは、次のように言い換えることができます。
1 + 1/2 + 1/3 + ... + 1/n > x
となる自然数 n が存在する。
この x について、補題2を満たす自然数 n のうち最小のものをとります。
このとき、y = x - ( 1 + 1/2 + 1/3 + ... + 1/(n-1) ) とおくと、
n の選び方により、 0 <= y < 1/n が成り立ちます。
この y を、補題1で与えられるアルゴリズムで単位分数の和に分解すると、
そこには、1/n 未満の単位分数しか現れないので、
1, 1/2, 1/3, ..., 1/(n-1) とは重複しません。
つまり、最初に与えられた x から、1, 1/2, 1/3, ... というふうに、
単位分数を大きいほうから順に引いていくと、
補題2によって、どこかでそれが続けられなくなりますが、
そのときの「余り」について、補題1を使えばよいわけです。

NO.261 '99 1/7 マサボー 分数の問題・その後(5) この問題を考える時、答えを求める他に次の2点にも
注目する必要があると思います。
それは、1)任意の分数(正の有理数)は単位分数の和として
表わすことが出来る、
2)その表わし方は無限に存在する、の2点です。
これらの提議は解答の中で証明されていると思いますが、
では実際の答えを示すにあたり
(今回の問題は2/3や4/5を単位分数の和で表わすこと)、
数学的に正しい解答を書くのはかなり難しいかったのではないでしょうか
(当然、答えが無限にある訳ですから)。
私が思うに数学は普遍性を重んじる学問ですから、
ある一定のプロセス(あるいは公式)を踏むことで
全ての答えが得られることが重要であり、
答えに「もれ」があってはならないと思います。
その意味から「水の流れ」さんの答えはかなり正解に近いものでしょう。
別のアプローチとして最初に方程式にて最少の単位分数の数を決め、
次に(最少+1)の単位分数の場合、
(最少+2)の単位分数の場合を各々方程式で求めるのも
答えを漏らさない方法の一つだと思います。
しかし、最初から最少の単位分数の個数を決める方法がない場合は
(私には分からなかった)、2個の場合、3個の場合と
「しらみ潰し」でやるしかないのかもしれません。
やはり数学も科学であり99%のperspirationが必須なのでしょう。

NO.280 '99 1/14 Idaho Poteto 分数の問題・その後(6) No.261で、マサボーさんは、
「分数の問題」に対する「数学的に正しい解答」とは何かを論じておられますが、
この点について、私はかなり異なる見解を持っています。
今回の問題は、「2/3, 4/5 を、相異なる単位分数の和で表せ」というものでしたが、
私は、問題文を読んで、単純に、
それを超える部分は、
あくまで、
それぞれの解答者による独自の拡張であって、
それはそれで大いに有意義なことではありますが、
問題に対する答としての「正しさ」とは別次元の話だと思います。
したがって、この問題の答としては、
少なくとも(たとえば)「2/3 = 1/2 + 1/6」「4/5 = 1/2 + 1/5 + 1/10」の2つの事実が述べられていれば、
それだけで完璧に「数学的に正しい」と考えます。
ついでに言うと、私は、
「1/2 + 1/6」「1/2 + 1/5 + 1/10」という具体的な解を「どうやって見つけたか」ということは、
その解答の「数学的な正しさ」とは無関係だと思っています。
つまり、たとえ「あてずっぽう」でそれらの解を見つけたとしても、
結果さえ正しければ、それは「数学的に正しい」、ということです。
このようなことを言うと、
見識高い「数学教育者」の皆さんのお叱りを受けるかもしれませんが、
数学一般において「正しい」とはそういうことである、
ということも、また事実なのです。
この問題が要求していることは、
2/3, 4/5 のそれぞれについて、
単位分数の和による表現を「少なくとも1通り」示すことである
と理解しました。
「すべての解を示せ」と明示的に要求していない以上、
このような解釈は、数学的に自然だと思います。
そして、その「拡張」の例として、たとえば
などがあるわけですが、
具体的に与えられた分数について、
単位分数の和による表現をもれなく検索するための手順を与える
ということもまた、その「拡張」のひとつとして評価されるべきだと思います。
もちろん、より一般性のある解法を示すほうが、
「より多くの拡張の可能性が生じる」という意味において有益であることは、
私も十分承知しています。
しかし、そのことと、
答としての「正しさ」とは、別の問題であると理解しています。

NO.281 '99 1/14 Idaho Poteto 分数の問題・その後(7) 前項に関連する問題提起です。
次のような問題を考えます。
この問題に対する解答例を2つ示します。
どちらのほうが、より「数学的に正しい」解答といえるでしょうか?
したがって、命題「x2 > 4 ならば x > 2」は正しくない。
したがって、命題「x2 > 4 ならば x > 2」は正しくない。

NO.287 '99 1/17 水の流れ 分数の問題・その後(8) NO.281について、
<解答1>はこれは数学的にいわゆる演繹法という
解答方法です。
<解答2>はこれは数学的にいわゆる帰納法という
解答方法です。1つでも反例があればそれは命題
として「偽」ですから、この証明も可です。
だから、優劣はつけられません。
したがって、いずれも「正しい」のです。

NO.293 '99 1/19 Junko 分数の問題・その後(9) 12月に出題した分数の問題についてです。 かつて、フェルマは NO.281については、
どちらももちろん正しいわけです。
「Idaho Poteto」さんのおっしゃるように
単位分数の和による表現を「少なくとも1通り」示していただければ、
正解と考えて出題しました。
(それ以上のことも内心期待はしていましたが・・・。)
「マサボー」さんは、私が出題した問題としてではなく、
もっと広い意味で「任意の分数(有理数)を単位分数の和として表すこと」
と考えているのではないでしょうか。
「22n+1という数はn=0,1,2,・・・に対して
素数を与える」と考えました。
これらの数はフェルマ数と呼ばれ、Fnと表されます。
F0=21+1=3
F1=22+1=5
F2=24+1=17
F3=28+1=257
F4=216+1=65537
でいずれも素数です。
しかしながら後にオイラ−が、F5が合成数であることを見つけました。
F5=232+1=4294967297=641×6700417です。
おそらくフェルマは上記の命題を証明しようと試みたのでしょうが、
反例を1つでも見つけてしまえばそれでおしまいです。
天才(?)は別として、
いきなり「解答1」のような答え方をするのはむずかしいと思います。
やはり最初は「解答2」のように具体的に考えてみるのがいいと思うし、
生徒に説明するような場面では納得もしてもらえると思います。
「解答1」の方がかっこいいという雰囲気があるような気もしますが、
これが数学嫌いを生んでいるような気もします。
問題に取り組む時も、具体的なモデルをたくさん知っていた方が、
その問題の理解に役立つと思います。
ただし命題を覆すなら反例1つで充分ですが、
命題を証明する時は具体例をたくさん示してもだめなのはもちろんです。

NO.306 '99 1/22 Idaho Potato 分数の問題・その後(10)
No.281については、
残念ながら、私の問いかけの意図が伝わらなかったようですね。
解答1は、数学的に厳密に言うと、問題に対する答になっていないのです。
解答1を数学的に正しく完成するためには、
「x < -2 または x > 2」が「x > 2」の十分条件でないこと、
すなわち、
「x < -2 または x > 2」を満たすが「x > 2」を満たさない実数 x が存在することを(たとえば「x = -3 がそうである」という形で)述べなければなりません。
No.293の後半の、Junkoさんのご意見について。
要するに、「何かが存在することを示す」ためには、
その「存在する」というものの具体例を実際に示してみせれば、それで十分であって、
その具体例を「どうやって見つけたか」ということは、
数学的には「二の次」ということですね。
その意味では、
今回の「分数の問題」のような「存在を示せば十分」というタイプの問題に対して、
「その答に到達するまでの過程」を書くことを要求することは果たして妥当なのか、
ちょっと疑問を感じてしまいます。
私のように、たまたま「目の子」で答を見つけてしまった人は、
「答に到達するまでの過程」の書きようがありませんから。
なぜなら、解答1の1行目は、
命題の仮定「x2 > 4」を同値な条件「x < -2 または x > 2」に言い換えているだけで、
その言い換えられた形の仮定と、
もとの命題の結論「x > 2」との間の関係について、
一言も述べていないからです。
つまり、「したがって」という言葉の前後に、脈絡がないのです。
それをするぐらいなら、
解答2のように、最初から天下りに具体的な反例を与えるほうが、
すっきりした答になるわけです。
私の印象では、むしろ、
「受験のための数学」に毒されている多くの高校生や大学生は、
問題の意味を考えずに等式や同値変形といったテクニックで答を得ようとして、
いきおい解答1のような答になり、
解答2のような答え方に思い至らないのではないかと思います。
すでに述べたように、解答1はかっこいいように見えて、実は中身がないのです。
それに対して、解答2は、問題の意味をちゃんとわかっている人の答え方といえます。

 戻る
戻る