Weekend Mathematics�^����^���39
�R�X�D���Z�p�`�̖��

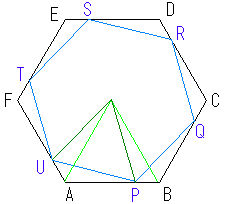
�P�ӂ̒������Scm�̐��Z�p�`�`�a�b�c�d�e������܂��B
�e�ӂ`�a�A�a�b�A�b�c�A�c�d�A�d�e�A�e�`��ɁA
���ꂼ�꒸�_�`�A�a�A�b�A�c�A�d�A�e����Rcm�̂Ƃ����
�_�o�A�p�A�q�A�r�A�s�A�t���Ƃ�A
����������ŘZ�p�`�����܂��B
���̂Ƃ��Z�p�`�o�p�q�r�s�t�̖ʐς́A���Ƃ̘Z�p�`�`�a�b�c�d�e�̖ʐς̉��{�ɂȂ�܂����B
�Z���P�O�O�̓��E���part�R
�����`��
�u�k�Ѓu���|�o�b�N�X
���z��
�i�y���l�|���F�l�h�m�h�l�h�m�h�R�Q�j
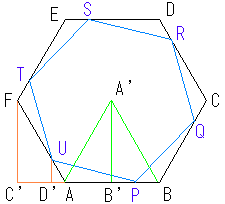
�܂����Z�p�`ABCDEF�̖ʐς����Ƃ߂܂��B
�i�Z�p�`�̒��_��A'�Ƃ��A��AB�̒��_��B'�Ƃ���j
���`�a�`�f�͐��O�p�`�Ȃ̂Ł�AB'A'��AA'��
�Scm�AAB'���Qcm�AA'B'���Q �ɂȂ�B
�ɂȂ�B
����ĘZ�p�`ABCDEF�̖ʐς͂S�~�Q ���Q
�~�U���Q�S
���Q
�~�U���Q�S �ƂȂ�B
�ƂȂ�B
���ɓ_�e���琂���ɂ��낵�����Ɛ�AB�̐����ɂ̂������Ƃ̌�_��C'�Ƃ����
��FAC'���U�O���A��AC'F���X�O���A��C'FA���R�O���ƂȂ�A
��AF���Scm�Ȃ̂Ő�AC'���Qcm�A��C'F���Q �ƂȂ�B
�ƂȂ�B
FU�FAU���R�F�P�Ƃ������Ƃ�U���琂���ɂ��낵�����Ɛ�AC'�Ƃ̌�_��D'�Ƃ����
��UD'�� /2cm�A
�܂���PD'��7/2cm�A����Đ�PU��
/2cm�A
�܂���PD'��7/2cm�A����Đ�PU��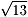 cm�B
cm�B
����ĘZ�p�`PQRSTU��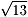 �~��39/2
�~(1/2)�~�U��(�R�X
�~��39/2
�~(1/2)�~�U��(�R�X /2)/2�B
/2)/2�B
�i�j
�Z�p�`ABCDEF�F�Z�p�`PQRSTU���P�U�F�P�R

�i�y���l�|���F�Ђ�䂫�j

�O�p�`�`�o�t�ƍ����ȘZ�̉s�p�O�p�`
�����Ђ������Ă��Ă������ĎO�̕��s�l�ӌ`��
���B
���s�l�ӌ`�́A�P�Q�O�x�ƂU�O�x�̊p�����B
�ӂ̒������킩���Ă���̂ŁA���̖ʐς� 3 /2�@�ƂȂ�
/2�@�ƂȂ�
�i�ȉ��ʐϒP�ʂ͂��ׂĕ����Z���`���[�g���j
���̐��Z�p�`�̖ʐς� 4 �~6�@���@24
�~6�@���@24 �ŁA
�ŁA
�������Ȃ������Z�p�`�̖ʐς�
24 �|3
�|3 /2�~3��39
/2�~3��39 /2�@�ł���B
/2�@�ł���B
����āA�Z�p�`�o�p�q�r�s�t�̖ʐς́A
���Ƃ̘Z�p�`�`�a�b�c�d�e��
39 /2��24
/2��24 ��39/48��13/16�{�@�|�i���j�@
��39/48��13/16�{�@�|�i���j�@

�i�y���l�|���F���j
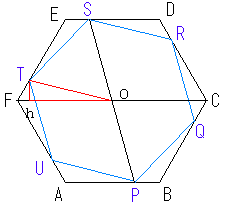
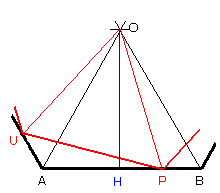
�Q�̐��U�p�`�̊O�ډ~�̒��S��O�Ƃ��A
T����OF�ɐ������~�낵�A���Ƃ���B
��O�s���̓����̂Q�̂R�p�`�ɂ��āA
�R�����̒藝�𗘗p����B
��TF���́A��TF����60���̒��p�O�p�`������A
��T����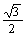 �A��F���� 1/2 �ƂȂ�A
OF=4���AO���� 7/2
�A��F���� 1/2 �ƂȂ�A
OF=4���AO���� 7/2
OT2=Th2+Oh2 ���A
OT2=(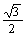 )2+(7/2)2=52/4
)2+(7/2)2=52/4
�܂��A��EOF�Ɓ�STO�͂Ƃ��ɐ��O�p�`������A������� OF:OT
�ʐϔ��OF2:OT2
����āA 42:52/4=64:52=16:13
�Z�p�`�o�p�q�r�s�t�̖ʐρF�Z�p�`�`�a�b�c�d�e���P�R�F�P�U�@�@�@�@

�i�y���l�|���F���j
��@�P
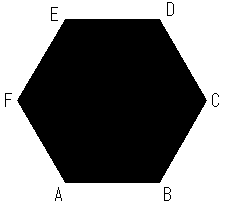
�ЂƂڂ͑f���ɖʐς����߂Čv�Z������̂ł��B
�P�ӂ��S�����̐��Z�p�`�ł��̂Ŕ�r�I�ȒP�ɂł��܂��B
���̍��h��S�̖̂ʐς́E�E�E���O�p�`���U����܂��B
���O�p�`�̍����͂Q ������
�ʐς͂S�~�Q
������
�ʐς͂S�~�Q �~�P�^�Q���S
�~�P�^�Q���S
���ꂪ�U�ł��̘Z�p�`�͂Q�S c�u
c�u
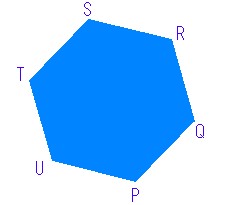
���ɏ��������̐��Z�p�`�ł����E�E�E
������̖ʐς́E�E�E�܂��P�ӂ̒������킩������̂ł����
���ׂ܂��B
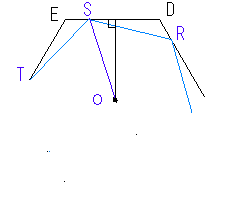
���S���n�Ƃ��Čv�Z����B
���R�n���炨�낵�������ł��邩��A�����d�c�̒��_��ʂ�B
����Đ����Ƃ̌�_�Ɠ_�r�܂ł́A�P�����B
�s�^�S���X�̒藝�������āE�E�E�n�r��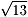 �ɂȂ�B
�ɂȂ�B
���ꂩ�獕�����Ɠ����悤�Ɍv�Z����Ɩʐς͂R�X �^�Qc�u�ł���B
�^�Qc�u�ł���B
����Đ��Z�p�`PQRSTU�͐��Z�p�`ABCDEF�̉��{���Ȃ̂ŁB
PQRSTU��ABCDEF���i�R�X �^�Q�j�^�i�Q�S
�^�Q�j�^�i�Q�S �j���P�R�^�P�U
���Ƃ������܂��B
�j���P�R�^�P�U
���Ƃ������܂��B
���Ȃ݂ɂ��̑O�̉͂��Ȃ�܂�肭�ǂ����Ƃ����Ă��܂��B
�{���́A�������ق��̂P�ӂ̒������킩��Ɠ����͏o�܂��B
�Q�̐��Z�p�`�͓��R�����ɂȂ��Ă��܂��B
����͑����䂪�킩��Ζʐϔ䂷���킩��̂ł��ˁB
������͂S�F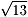 �ł��邱�Ƃ��킩���Ă���̂�
���R�ʐϔ�͂P�U�F�P�R�ɂȂ�܂��B
����Ă����̖��̓����͂P�R�^�P�U�Ƃ����킯�ł��B
�ł��邱�Ƃ��킩���Ă���̂�
���R�ʐϔ�͂P�U�F�P�R�ɂȂ�܂��B
����Ă����̖��̓����͂P�R�^�P�U�Ƃ����킯�ł��B

�i�y���l�|���Fmhayashi�j
����AD�Ɛ���BE�̌�_��_O�Ƃ���B
�O�p�`OAB�ƎO�p�`UAP�ɂ��čl����B
�O�҂̒��AB�ƌ�҂̒��AP�̔�͂S�F�R�ł���A
�܂��A�O�҂̍����ƌ�҂̍����̔�͂S�F�P�ł��邩��A
| �O�p�`OAB�F�O�p�`UAP | ��4�~4�F1�~3 |
| ��16�F3 |
| �Z�p�`ABCDEF�F�Z�p�`PQRSTU | ��6�~�O�p�`OAB�F6�~�O�p�`OUP |
| ��16�F13 |

�i�y���l�|���F��ӂ����̂炢��������j
�����́A�P�R�^�P�U�ł��B
�Ȃ��Ȃ�A
| �Z�p�`PQRSTU�^�Z�p�`ABCDEF | |
| �� | ��OUP�^��OAB |
| �� | UP2/AB2 |
| �� | OP2/OA2 |
| �� | (OH2+HP2)/42 |
| �� | ((2 )2+12)/42 )2+12)/42
|
| �� | 13/16 |

�i�y���l�|���F���j

�܂��A�����ɏo����Z�p�`�͐��Z�p�`�ł��B
����āA�O���̘Z�p�`�Ƒ����Ȃ̂ŁA�ʐϔ���o�����ɂ��܂��B
������͕ӂ̔�Ȃ̂ŁA�ӂ̒����̂Q������߂܂��B
���Z�p�`�̂P�̊p��120���Ȃ̂�(�ǂ��ł���������)�O�p�`UAP�ɑ��ė]��
�藝���g���ƁA
PU2 = AU2 + PA2 - 2�~AU�~PA�~cos120��
�ƂȂ�܂��B
�����Ŗ�蕶��� AU = 1 PA = 3 �ł���Acos120��= -1/2 �ł���̂ŁA
PU2 = 1 + 9 - (-3) = 13 �ƂȂ�܂��B
����ŁA�����̘Z�p�`�̕ӂ̒����̂Q�悪���܂�܂����B
�܂��A�O�̘Z�p�`�͈�ӂ̒�����4�Ȃ̂ŁA�Q�悵��16�ƂȂ�̂ŁA
�ʐϔ�c�c �O�F�� �� 16:13
����āA���̘Z�p�`��13/16�{�ɂȂ�B

�i�y���l�|���Fch3cooh�j

����:13/16
 /4)2= 13/16 (answer)
/4)2= 13/16 (answer)

�i�y���l�|���Fkiyo�j

���Ƃ̐��Z�p�`�̂U���̂P�̐��O�p�`�̖ʐς��P�Ƃ���B
���ϕϊ��̍l�����ɂ��ƁA�V�����o�������Z�p�`�̂U���̂P�̐��O�p�`�̖ʐς́A
�Q�|�i�P�{(1/4)�~(3/4)�j��13/16
���������āA���߂铚����13/16�{�ƂȂ�B
�����@�P�R�^�P�U�{

�i�y���l�|���FsambaGREEN�j

��UAP�F��FAB���P�~�R�F�S�~�S���R�F�P�U
��FAB�͘Z�p�`�`�a�b�c�d�e�̂U���̂P��
��UAP�͘Z�p�`�o�p�q�r�s�t�ƘZ�p�`�`�a�b�c�d�e�̍��̂U���̂P�ł�
���������āC�Z�p�`�o�p�q�r�s�t�F�Z�p�`�`�a�b�c�d�e��(16-3):16���P�R�F�P�U
�����E�E�E13/16�{

�i�y���l�|���FIdaho Potato�j
(1)�́u�܂�����������߂�v�Ƃ������_����̉A
(2)�͍ŏ�����u�ʐϔ�v�ɒ��ڂ����ɂȂ��Ă��܂����A
�ǂ��炪�u�f���ȁv�Ƃ�����ł��傤��?
���͍ŏ���(1)�̉�@���v�������̂ŁA
(2)�͂���߂ċZ�I�I�Ȋ����������̂ł����A
���炽�߂čl���Ă݂�ƁA
�L�����̌v�Z�݂̂ŗL�����̉��ɂ��ǂ蒅��(2)�̂ق����A
����Ӗ��Łu�f���ȁv��@�ł���悤�ȋC�����Ă��܂����B
(1) �s�^�S���X�̒藝���g������
(�P��cm�͏ȗ�)
�Z�p�`ABCDEF�̊O�ډ~�̒��S��O�AO����AB�ւ��낵�������̑���H�Ƃ���B
���̂Ƃ��A OA = 4, AH = 2, HP = 1 �ł���B
OH = sqrt(OA2+AH2) = 2
OP = sqrt(OH2+HP2) = 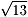
�䂦�ɁA�Z�p�`PQRSTU�ƘZ�p�`ABCDEF�̑������
OP/OA = 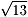 /4�ł���B
/4�ł���B
�ʐϔ�͑������2�悾����A(�Z�p�`PQRSTU)/(�Z�p�`ABCDEF) = 13/16�ł���B
�@
(2) ���w�Z�̎Z���͈̔͂ł̉�
�Z�p�`ABCDEF�̊O�ډ~�̒��S��O�Ƃ���B
���߂�ʐϔ�� ��OPQ/��OAB �ɓ������̂ŁA��������߂邱�Ƃ��l����B
���̎�����p����B
�u�������������O�p�`�̖ʐϔ�́A��ӂ̒����̔�ɓ������B�v
��OBQ �� ��OAP ���A ��OAB = �l�p�`OPBQ = ��OPQ + ��PBQ
�܂��A��OAB = ��ABC (AB�����ʂ̒�ӂƂ݂�ƍ�����������)
�䂦�ɁA��OPQ = ��ABC - ��PBQ �ł���B
| ��PBQ | = (BQ/BC)��PBC (BQ,BC���ӂƂ݂�ƍ�����������) |
| = (BQ/BC)(PB/AB)��ABC (PB,AB���ӂƂ݂�ƍ�����������) | |
| = (3/16)��ABC |

�i�y���l�|���F���̗���j
�P�ӂ��S�����̐��Z�p�`ABCDEF�Ɓ@���Z�p�`PQRSTU�͓��p�����ׂĂP�Q�O�x������ �����ł��B����āA�P�ӗႦ�AUP�̒��������߂܂��B �����l����A���Z�����Ɏv�����܂����B�������A���w�Z�������ł�����A ���w�Z�̍l�����ł��傤���A�Ƃ肠�����A���Z�̍l�����ł����܂��B

�`�i�O�{���O�j�C�a�i�S�{���O�j�Ƃ����ƁA���炩�ɁA�o�i�R�{���O�j�C
�܂��A�t�̍��W�́icos120�K+i sin120�K)=(-1/2�{i /2)
/2)
| ����āA��UP�� | �����i�i�R�{���O�j�|�i-1/2�{i /2�j�� /2�j��
|
�����i�i�V/2�|i /2�j�� /2�j��
| |
| ����i�S�X�^�S�{�R�^�S�j | |
��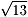
|

�i�y���l�|���F�l�c�@�����j
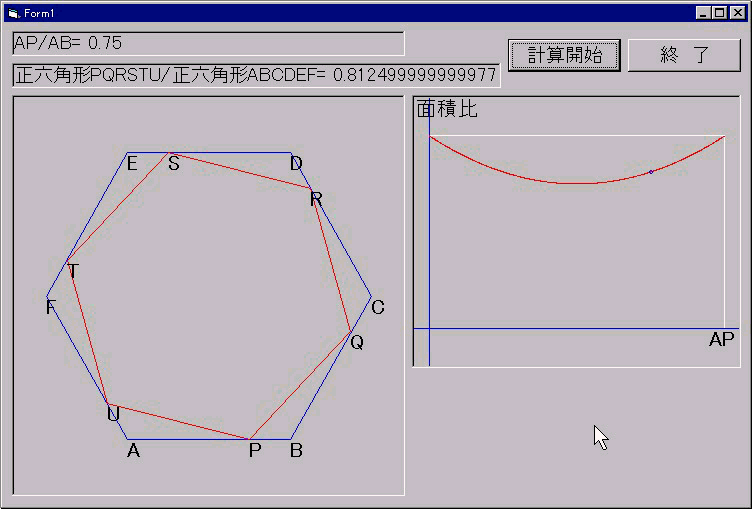
�����̂悤�Ƀp�\�R���Ő}��`���v���O����������Ă݂܂����D
�ӂ`�a���_�o���`����a�܂ňړ����C�`�o���R�ƂȂ�Ƃ��̖ʐϔ���v�Z���܂�
�i�{���́C�n�𐳘Z�p�`�̒��S�Ƃ���Ƃ��̂n�o2�^�n�`2���v�Z���邾���Ȃ̂ŁC
����ȑ傪����Ȃ��̂ɂ���K�v�͂Ȃ������̂ł����j�D
���̃v���O�����ɂ��C���͂O.�W�P�Q�T�i���P�R�^�P�U�j�ƂȂ鎖��������܂��D

| kiyo | ���NH | sambaGREEN |
| ch3cooh | ��ӂ����̂炢�������� | ���� |
| mhayashi | ���̗��� | �l�c�@���� |
| Idaho Potato | �� | MINIMINI32 |
| �Ђ�䂫 | �� | �g�V |
| �}�T�{�[ |

�����������}�`�̖��͉�@�����������āA�����������Ӗ��ł������낢�Ȃ��Ǝv���܂��B
�E���̂S�ł���������������Ă���悤�ɁA
�����Ȑ}�`�ɂ����ẮA�ʐϔ���o�����߂ɖʐςڏo���K�v�͂Ȃ��A�����䂪�킯����̂Q��ŋ��߂邱�Ƃ��ł��܂��ˁB
�������̐ϔ�Ȃ�R��ł��B
�����E���̂P�P��Idaho Potato�Ɠ����ŁA
�����������@�̒��ŁA�O�p�`�̒�ӂ̒����ƍ����̔�ŏo���Ă�����̂�
�����Ƃ��V���v���ł��ꂢ���ȂƊ����܂��B
�E���̂X��kiyo����́A��{�I�ɂP�s�ʼnɎ����Ă��܂��B
���w���̒m���ʼn�����Ƃ������Ƃ�����܂����A����͊��o�I�Ȃ��̂�������܂���̂ŁA
�l�ɂ���Ċ������͈Ⴄ��������܂���B
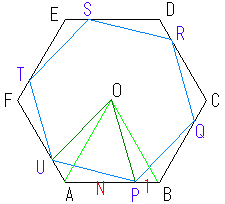
���̉�@�ŁAAP:PB=3:1�@����ʉ����Ă݂܂��B
AP:PB=N:1�@�Ƃ��܂��B
��UAP=(N/N+1)�(1/N+1)��OAB
��OCP={1-(N/N+1)�(1/N+1)}��OAB
�]���āA������1-(N/N+1)�(1/N+1)=(N2+N+1)/(N+1)2 �ƂȂ�܂��B
���̃O���t���umathematica�v�ŕ`���Ƃ����Ȃ�܂��B
�������N=1�ŋɏ��ŁA�ɏ��l3/4�ł��B
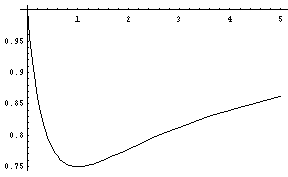
�@
�֘A�����b�肪�A
�R���L�E���� NO.793�ɂ���܂��B

 E-mail
E-mail
 �߂�
�߂�
 �z�|���y�|�W
�z�|���y�|�W