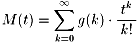
となる予定です。
これが無限級数の和の発展になっていたのです。でも、自信がないです。
Weekend Mathematics/コロキウム室/2000.1〜3/NO.90
| NO.777 | 2000.3.9. | 水の流れ | 無限級数の和(13) |
午後、勤務先で「コロキウム室」の
NO.776 無限級数の和(12)
の投稿を読んで、大変興味が湧いてきました。
実は”あの第2種スターリング数”の一般項を見つけるもう1つの方法が、
指数型母関数(積率母関数)の登場なのです。
そして、k次の中心積率(モーメント)を定義します。この値をH(k)とします。
さらに、特別な原点のまわりのk次の積率を出し、この値をh(k)とします。
すると、h(1)=期待値E(X)=1、H(2)=分散V(X)=1となります。
そして、h(k)が何とビル指数となっています。指数型母関数(積率母関数)の定義から導けます。
ここで、確率変数Xの指数型母関数(積率母関数)とは、M(t)=関数etxの
期待値が−h<t<h(hは正の定数)を満たす原点近傍のすべての実数tに対して存在するとき、
M(t)=E[etx](平均)を言います。
以上は、「新数学辞典」(大阪書籍)から答えています。
さらに、このことは、
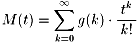
となる予定です。
これが無限級数の和の発展になっていたのです。でも、自信がないです。
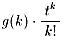 の係数がh(k)になっているか確かめていません。これも勉強します。
の係数がh(k)になっているか確かめていません。これも勉強します。
午後、この示唆をくださったとき、当然太郎さんの胸に熱いもの湧いてきたのは当然でした。
頭の片隅にはこのk次のモーメントの言葉がかすかに残っていました。
心のゆとりが欲しい! ありがとう!ヴァーさん

| NO.778 | 2000.3.10. | kiyo | 階乗関数(3) |
Stirling numbers of 2nd kind の一般項を十進ベーシック(1000桁モード)で
プログラムしてみました。
REM Stirling numbers of 2nd kind 一般項の計算
10 INPUT PROMPT "行n, 列 k:k<=n ":N,K
IF K>N OR K<=0 THEN
PRINT "正しく入力して下さい"
GOTO 10
ELSE
PRINT "計算を開始します。"
END IF
DIM S2(N,K)
LET S=0
FOR I=1 TO K
LET S=S+(-1)^(K-I)*COMB(K,I)*(I^N)
NEXT I
REM K!の計算
LET S1=1
FOR J=1 TO K
LET S1=S1*J
NEXT J
LET S=S/S1
PRINT "S2(";N;",";K;")";"=";S
END

| NO.779 | 2000.3.12. | WAHEI | ガロア理論の心(3) |
(群指標とその独立性)
ここではガロアの基本定理を解く鍵となる、指標の独立性を考えます。
そこで群の準同型写像を定めましょう。といっても別に新しい事ではありませんが…
(定義)
AとBを積で群とする。
写像f:A→Bが群の準同型写像であるとは、f(ab)=f(a)f(b)を満たす事を言う。
従ってeをAの単位元、e´をBの単位元とするなら、f(e)=e´が成り立つ。
一般に演算を保つものを準同型写像と言いました。
ですから、環写像はもちろん準同型写像です。
ここで、体は積でアーベル群を成していましたから、
群Gと体kの間に矛盾なく群の準同型写像を定められるはずです。
この群から体に向かう群の準同型写像を体kにおける群Gの指標といいます。
定義を厳密に書くと次のようになるでしょう。
(定義)
G´={σ|σ:G→kで群の準同型写像}として、
∀α∈Gに対しσ(α)≠0を仮定する。このσを体kにおける群Gの指標という。
今は演算は積としていますから、σ(α)=0では意味を成さない事に注意してください。
さて、次に書くのが有名な指標の独立性です。
(定理)…指標の独立性
σ1……σn∈G´を相異なる群指標とする。
(つまり写像として異なっている)このとき
α1σ1(x)+…+αnσn(x)=0
(∀αi∈k、∀x∈G)ならば、α1=…=αn=0が正しい
(但し1≦i≦n)
つまり指標によって移されたGの元は体k上で1次独立になっているということです。
この証明はArtin先生のうまい方法に従いましょう。
(Artin先生の証明)
nに対する帰納法で示す。
n=1の時はα1σ1(x)=0で、
σ1(x)≠0であり、
体は全て整域なのでα1=0であるから成り立つ。
だからn>1として、n−1まで定理の主張が正しいとする。
今yをGから任意にとってxとの積yxを考えると群は演算が備わっているので
当然このyxもGの任意の元である。
そこで、xをyxに置き換える。すると、
α1σ1(yx)+…+αnσn(yx)=0
であって、今σ達は群の準同型なので、
α1σ1(y)σ1(x)+…+αnσn(y)σn(x)=0となる。この式を(1)とおく。
さて、ここで元の式、つまり
α1σ1(x)+…+αnσn(x)=0の両辺にσn(y)をかける。
すると、
α1σn(y)σ1(x)+…+αnσn(y)σn(x)=0
となり(なぜならσは準同型写像なので)この式を(2)とおく。
さて、ここで(1)−(2)を実行する。すると、n番目の項が打ち消される。
α1σ1(x)(σ1(y)−σn(y))+…+αn−1σn−1(x)
(σn−1(y)−σn(y))=0
従って帰納法の仮定により特にα1(σ1(y)−σn(y))=0としてよい。
今はn>1なので、
σ1(y)とσn(y)は等しくないから、
α1=0である。
よって以下同じようにα2=α3=…=αn−1=0なので、αn=0
となる。 (証明終わり)
どうでしょうか?いつ考えてみても非の打ち所のない完璧な証明です。
この指標の独立性のコロラリーとして、次の補題を得ます。
(補題1)
体KとLに対してσ1、σ2、…、σn:K→Lを相異なる環写像とすると、
α1σ1(x)+…+αnσn(x)=0ならば、
α1=α2=…=αn=0である。
(但し∀αi∈K、∀x∈Gで1≦i≦n)
この補題はDedekind(デデキント)の補題と言われています。
(スペリングは自信ありません)証明はもう済んでいます。なぜなら環写像は群の準同型となるからです。
さて、僕自身も大分忘れかけていますから、復習をしながら進んでいきましょう。
方程式上の分解体をEとし、その自己同型群AutEを考えます。
GをAutEの部分群とし、E(G)はGの元(写像)で動かないEの元の集合で、
Gに対する不変体と言いました。
またこのE(G)はEの部分体になっている事はすぐにわかります。
ですから、体の拡大E/E(G)を得ます。ではこの拡大次数はどうなっているでしょうか?
つまり、[E:E(G)]を求めたいのです。
(補題2)
G={σ1、σ2、…σn}とおく。すると、[E:E(G)]≧nが正しい。
この補題がいっている事を整理してみますと、AutEの部分群Gが上のようにn個の元から成っていれば、
体の拡大E/E(G)の拡大次数は少なくともnよりは大きい、
つまり、|G|より大きいと言っています。本当でしょうか?
(補題の証明)
背理法で示す。すなわち[E:E(G)]=r<nとして矛盾を導く。
[E:E(G)]=rで、これはE(G)上のベクトル空間Eの次元を表していて、
次元とは一次独立なベクトルの最大個数であった。
これらのベクトルをベクトル空間Eの基底という。
従って基底の個数とベクトル空間の次元は一致する。
さて、Eの基底は今r個あるのでその基底を1組持ってくることができ
(基底の取り方は一意的ではありません。よく知る2次元の平面で考えるとわかります)、
それらを{ω1、ω2、…ωr}とする。(基底はこのように集合の形で書く)
ここで次の連立方程式を考える。
σ1(ω1)x1+σ2(ω1)x2+…+σn(ω1)xn=0 …………… σ1(ωr)x1+σ2(ωr)x2+…+σn(ωr)xn=0この連立方程式は未知数、つまりxの個数がn個で方程式の個数がr個、 従ってr<nを考えればこの連立方程式は非自明な解を持つ(これについてはこの証明が終わってから解説します)。
σ1(a1ω1)x1+…+σn(a1ω1)xn=0 ……… σ1(arωr)x1+…+σn(arωr)xn=0これらの式を一斉に加え、 かつα=a1ω1+…+arωrを考え 次の式を得る。
さて、ガロア理論の本質というのは分解体上の自己同型群の部分群と分解体以下の中間体との間に
一対一対応があるということでした。
実はこれはどんな体拡大に関してもいえるわけではありません。
今まで取り上げた例は全てある特殊な拡大になっていたのです。
(定義)…ガロア拡大
K/Fを体の拡大とする。
この拡大がガロアである(またはガロア拡大である)とは、F=K(G)となるAutKの部分群Gが取れることを言う。
今まで考えてきた事によるとAutKの部分群としてGal(K/F)が取れていたわけです。
さらに上で示した補題2を芸術にまで昇華した定理として次を挙げる事ができます。
(ガロアの定理)
補題2と同じ仮定でGが有限群ならば、[E:E(G)]=|G|が成り立つ。
(証明)
補題2より、[E:E(G)]≧n=|G|は言えている。
示すべきは[E:E(G)]≦nである。
これを示すにはα1、α2、…αn−1∈Eが常に一次従属である事を言えばいい。
G={σ1、σ2、…σn}とする。
ここで補題2と同じ方針で非自明解をもつ連立方程式を作ることを考える。
そこでつぎの方程式を考えるとうまくいく。
σ1−(α1)x1+…+σ1−(αn+1)xn+1=0 ……… σn−(α1)x1+…+σn−(αn+1)xn+1=0
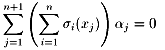 となる。
となる。
ここでx1≠0より、σ1(x1)≠0であって、
よってこれはα1、α2、…αn+1が一次従属である事を示している。
従って[E:E(G)]=|G|を得る。
(証明終わり)
この等式、つまりGが有限群ならば、[E:E(G)]=|G|は有名なオイラーの公式と同等に美しい公式として知られ、
大学の学部のレベルで理解できる数学としては最も綺麗な公式とされています。
このガロアの定理のコロラリーとして、次を得ます。
(コロラリー)
Gal(E/E(G))=G
この等式も実に綺麗です。全く感動物ですね!
(補題)
G1、G2<AutEを2つとも有限部分群とする。
このときG1=G2⇔E(G1)=E(G2)
(証明)
まず⇒は全く自明。問題は逆方向です。
G1=Gal(E/E(G1))=Gal(E/E(G2))=G2
従ってG1=G2を得ます。これはすぐ上のコロラリーを使えば割りと簡単ですね。 (証明終わり)
これによるとガロアの理論(すなわち分解体上自己同型群の部分群と中間体の間に一対一対応が存在)において、
AutEの部分群Gは拡大E/Fに対して唯1つ定まり、
G=Gal(E/F)であると言っています。
それでは、いよいよガロアの基本定理を料理しましょう。
(ガロアの基本定理の前半…Fundamental Galois Theorem Stage 1)
K/Fを有限次のガロア拡大とする。
このときK/Fの中間体の集合AとG=Gal(K/F)の部分群の集合Bの間には
次のような一対一対応がつく。
m:A→B
n:B→A
でn(m(A))=A(つまり写像nとmの合成がA上の恒等写像)かつ、
m(n(B))=B(つまり写像mとnの合成がB上の恒等写像)
ガロアの基本定理というのはこの前半と後半を合わせた物ですが、
後半の証明は次回に回して(申し訳ありませんがベクトル空間の基本概念も次回に回します)、
今回はこの前半の証明をやって終わりましょう。
(前半の証明)
m(n(B))=Bはつまり、∀G∈Bに対してmn(G)=GということなのでGal(K/K(G))=Gであって、
ガロアの定理とそのコロラリーから成立している。(うまい対応がすでについていましたね)
n(m(A))=Aが問題である。
これは∀E∈Aに対してnm(E)=Eということなので、K(Gal(K/E))=Eを示せばいい
(なぜならば、不変体というのは分解体の中間体でしたから)。
ここでK(Gal(K/E))⊇Eは明らかである
(不変体とガロア群の定義からこれは明らかとしていいと思うのです。
でも腑に落ちない方はきちんと納得がいくまで考えてください)。
従ってK(Gal(K/E))⊆Eを示せばいい。
便宜上、H=Gal(K/E)とおき、またE´=K(H)とおく。
ガロアの定理とそのコロラリーからK/K(H)は有限次ガロア拡大であって、
従って[K:K(H)]=|H|が成り立つ。
ここで体の拡大次数の関係式[K:F]=[K:E´][E´:F]
(これはNO.771 ガロア理論の心(2)で書いたと思うのですが、その証明はまだやっていませんでした。
次回にやりたいと思います)と、
群の指数と位数の関係式
|G|=|H|[G:H]
(これは代数方程式シリーズでやりました。
ここで紛らわしくて恐縮ですが[G:H]は体の拡大次数ではなく、
群GのHに関する指数です)
はガロアの理論によると対応しているから
(ここが本質的です。すなわち体の拡大次数と群の指数は対応しているのです)、次を得る。
[E´:F]=[K:F]/[K:E´]=|G|/|H|=[G:H]
従って[E´:F]=[G:H]=rとおいてGを同値類に分解する。
(この話は全て代数方程式シリーズに書いてあります。忘れた方はもう一度見直してみてください)
G=a1H∪a2H∪…∪arH
ここでaiは全てGの元であって、よって写像である事に注意する。
(1≦i≦r)このai達をE上へ制限する。
但し、写像の制限とは、写像f:A→Bがあって、CをAの部分集合とすれば、
f|C;C→Bとして、写像fをCへ制限するという。
すなわちAの部分集合Cの元をfでBへ移す事をいう。
さて、a1|E、a2|E、…ar|E :E→K相異なる。
なぜならば、ai(α)=aj(α)が∀Eについて成り立つなら、
aj−aiはEの元を固定するK上自己同型なので、
aj−ai∈Hとなって
これはG上の同値関係R11となっている
(代数方程式シリーズ参照)ので、
ajとaiは同じ同値類に属している(分割の補題より)から、
i=jとなる。従ってガロアの定理から
[E:F]≧r=[E´:F]であるからE=E´がわかる。 (証明終わり)
正直にいうと、今回の内容はかなり高度です。
さすがにガロアの理論と言われるだけあるでしょう。
もちろん一回読んだだけでは意味がさっぱりわからないと思っております。
何回も自分がわかるまで読んでみるといいでしょう。
ですから何も僕のやり方でなくともいいわけです。
ベクトル空間の内容はともかくとして、それ以外は全て今まででやってきた事ですから、
わからなくとも悲観する事をせずに、
特に代数方程式シリーズを読み直してみるといいでしょう。
次回にこのガロアの基本定理の後半を示して、ベクトル空間の基本性質を簡単に紹介して可解群に入りたいと思っております。

| NO.780 | 2000.3.12. | ちか | 3倍角の公式(1) |
tan3θ = (3tanθ-tan3θ)÷(1-3tan2θ)
って言うのを、
cos3θ = 4cos3θ - 3cosθ
son3θ = 3sinθ - 4sin3θ
を使って、証明しなければならないんですが、
どうやればでしょうか?
tanθ を sinθ÷cosθ
に置き換える方法をやってみたのですが、
どうしても、証明する事ができません。

| NO.781 | 2000.3.12. | Junko | 3倍角の公式(2) |
基本的には、tanθ = sinθ/cosθを使えばいいと思います。
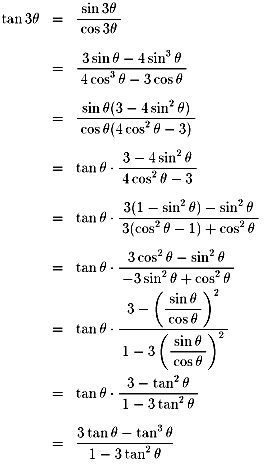

| NO.782 | 2000.3.12. | 水の流れ | 階乗関数(4) |
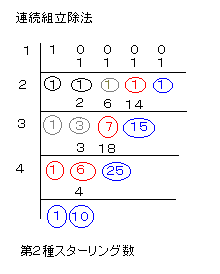
NO.774 階乗関数(1)で提起した問題ですが、
恒等式の性質で未定係数法を使って、
S(2,1)=1,S(2,2)=1,S(3,1)=1,S(3,2)=3、S(3,3)=1
と出します。
ここで、他の求め方もあります。それが、連続組立除法という方法です。
この方法は、整式Aを1次の整式Bで割った商をP、あまりをQとしたときに、
一度に求めてくれる方法です。
よく、因数分解するとき、1次因数を発見するのに使います。
詳しく左の図を見て下さい。
ご覧のように、次々と、「第2種スターリング数」が生まれてきます。
したがって一般に、xn=S(n,1)x[1]+S(n,2)x[2]
+S(n,3)x[3]+・・・+S(n,n)x[n]
となる係数S(n,1)、S(n,2)、S(n,3)、・・・、S(n,n)はこの連続組立除法で続けていけば、
簡単に求められます。
更に先の話は、
<美しい数学の話>第18話 「第2種スターリング数S(n,k)」にあります。

| NO.783 | 2000.3.12. | Iwasaki | 玉の選び方(1) |
5つの玉(青:3 赤:2)より2つ選んだ場合、2つとも赤い玉が選ばれる確率は?

| NO.784 | 2000.3.12. | Junko | 玉の選び方(2) |
5つの玉を{B1、B2、B3、R1、R2}とします。
まず可能性すべてを書き出してみます。
{B1、B2}、{B1、B3}、{B1、R1}、{B1、R2}、{B2、B3}、
{B2、R1}、{B2、R2}、{B3、R1}、{B3、R2}、{R1、R2}の10通りになります。
玉を選ぶ際に2つの玉の順番は関係ないので、集合の記号で書き表してあります。
これを「組み合わせ」と言います。
Combinationの記号を使って、5C2=10ともかけます。
一般に異なるn個の中から同時にr個取り出す組み合わせは、nCrとかき、
nCr=n!/r!(n−r)!で計算できます。
[nの階乗:n!=n・(n−1)・(n−2)・・・2・1]
さてこの10通りの中で、赤2つが取り出されるのは、{R1、R2}の1通りしかありません。
青を無視して、赤2つの中から2個取り出す場合の数、2C2=1と考えてもいいでしょう。
したがって確率は、P=1/10と考えられます。

| NO.785 | 2000.3.15. | 月の光 | 3倍角の公式(3) |
ド・モアブルの定理
(cosθ+isinθ)n=cosnθ+isinnθ
の左辺を展開し実部と虚部を比較するとn倍角の公式が得られます。
tannθ=sinnθ/cosnθとするとtannθもtanθだけの式で表わされます。
ガウス記号を使ってやってみて下さい。

| NO.786 | 2000.3.15. | 月の光 | dilogarithm |
M・ケッヒャーの数論的古典解析という本にこの関数が紹介されていました。
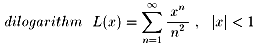
は次のような不思議な関係があります。
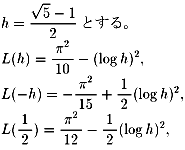
本に載っていたのは半ページ足らずの値の紹介だけで具体的な求めかたは
載っていませんでした。
この関数についてなにか御存知でしたら教えて下さい。

 E-mail
E-mail
 戻る
戻る