
Weekend Mathematics/コロキウム室/2000.1〜3/NO.88
| NO.761 | 2000.2.26. | kiyo | 無限級数の和(9) |
表を作りました。
| N/K | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 計 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | ||||||
| 2 | 1 | 2 | 3 | |||||
| 3 | 3 | 3 | 1 | 7 | ||||
| 4 | 4 | 6 | 4 | 1 | 15 | |||
| 5 | 5 | 10 | 10 | 5 | 1 | 31 | ||
| 6 | 6 | 15 | 20 | 15 | 6 | 1 | 63 | |
| 7 | 7 | 21 | 35 | 35 | 21 | 7 | 1 | 127 |
A(n)=SUM{C(n,k)}=2n-1
「水の流れ」さんの問題の趣旨は、
指数関数に関係していると同時に、
階差数列が循環しながら(再帰的に)現れるという点でしょうか?
1 2 3 4 5 6 7 1 1 1 1 1 1 ........................... 1 3 6 10 15 21 2 3 4 5 6 1 4 10 20 35 3 6 10 15 1 5 15 35 4 10 20 1 6 21 5 15 1 7 6

| NO.762 | 2000.2.26. | kiyo | 階段の問題(2) |
トリボナッチ数列の問題ですね。
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | |||
|---|---|---|---|---|---|---|---|---|---|
| 0 | 0 | 1 | 1 | 2 | 4 | 7 | 13 | 24 | 44 |

| NO.763 | 2000.2.26. | Junko | 階段の問題(3) |
この問題は、NO.219 バスケットボ−ルの問題と同じ問題ですね。
トリボナッチ数列については、NO.217 大相撲本場所(11)にあります。

| NO.764 | 2000.2.26. | kiyo | 無限級数の和(10) |
NO.756 無限級数の和(7)の
「n個の異なる要素を持つ集合を空でないk個の部分集合に分ける方法は何通りあり
ますか」
K個の部分集合の意味を取り違えていました。K個の要素を持つと勘違いしていました。
これで問題の趣旨が理解出来ました。
同値の問題ですね。
表
| N/K | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 計 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | ||||||
| 2 | 1 | 1 | 2 | |||||
| 3 | 1 | 3 | 1 | 5 | ||||
| 4 | 1 | 7 | 6 | 1 | 15 | |||
| 5 | 1 | 15 | 25 | 10 | 1 | 52 | ||
| 6 | 1 | 31 | 90 | 65 | 15 | 1 | 203 | |
| 7 | 1 | 63 | 301 | 350 | 140 | 21 | 1 | 877 |

| NO.765 | 2000.2.27. | Junko | 「三角の問題」の発展(2) |
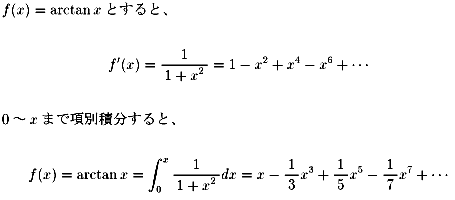
テイラ−展開については、
NO.376 ゼーター関数物語(22)にあります。

| NO.766 | 2000.2.27. | kiyo | 無限級数の和(11) |
表のなかに秘められた美しい規則性について。
表
| N/K | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 計 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | 1 | ||||||
| 2 | 1 | 1 | 2 | |||||
| 3 | 1 | 3 | 1 | 5 | ||||
| 4 | 1 | 7 | 6 | 1 | 15 | |||
| 5 | 1 | 15 | 25 | 10 | 1 | 52 | ||
| 6 | 1 | 31 | 90 | 65 | 15 | 1 | 203 | |
| 7 | 1 | 63 | 301 | 350 | 140 | 21 | 1 | 877 |
| k | ||||||
| 2 | 1, | 3=1*2+1, | 7=3*2+1, | 15=7*2+1, | 31=15*2+1, | 63=31*2+1 |
| 3 | 1, | 6=1*3+3, | 25=6*3+7, | 90=25*3+15, | 301=90*3+31 | |
| 4 | 1, | 10=1*4+6, | 65=10*4+25, | 350=65*4+90 | ||
| 5 | 1, | 15=1*5+10, | 140=15*5+65 | |||
| 6 | 1, | 21=1*6+15 |
上記の規則性をアピールされたかったのだと思います。

 E-mail
E-mail
 戻る
戻る