Weekend Mathematics／コロキウム室／テーマ別
／20.最速降下問題1
NO.415 '99 3/22 水の流れ ゼーター関数物語（４５）
ゼーター関数ζ（２）物語第１３夜＜特別寄稿＞の始まり、始まり。
さて、レオナルド・オイラーは広範囲に業績を残した
１８世紀を代表する数学者であります。
この物語の一部は、１７４８年に発表された
『無限小解析入門』の中に書いてあります。
また、オイラーの数学について語ろうとすると、
いずれにしても彼の論文の全集「オペラ・オムニア」全７３巻にふれないわけにはいきません。
これは彼が生涯に著した８８６篇にもおよぶ論文
（ラテン語、フランス語、ドイツ語などさまざまな言語で書かれています）をおさめたものです。
作品の幅は広く、相当なものでしたから、未発表のまま残されていたものを出版するのに
死後４７年間もかかったと言われています。
それらには偏微分からグラフ理論、複素解析、常微分方程式に至るまで
数学の全領域にそれぞれ新しい方向を示した独創性あふれる論文が入っているのです。
実際、あらゆる数学の分野にオイラーに帰される重要な理論が存在します。
したがって私たちはオイラー定数、オイラーの多項式、オイラー積分等々の存在は
もちろん、幾何学ではオイラーの三角形、位相幾何学では、オイラーの標数、グラフ
理論ではオイラーの閉路といった具合にあちこちでその名を見出すことになります。
ここで、「数学の知性」を読んでいて、興味深い問題がありましたので、
紹介します。
それは、ヨハン・ベルヌーイが１６９６年７月にライプニッツの雑誌
“ActaEruditorum”に手強い問題を発表しました。ヨハン自身こう述べています。
『気高く、独創的な精神は知識を増やすための努力を引き出すものであるが、
これを強く刺激するものとしては、難解でしかも役に立つ問題を求め、
これを解くことで名声を獲得し後世に永遠の記念塔を残すこと・・・、
これ以上のものはほとんど考えれない。それは周知のことである。』
ヨハンの考え出した特別問題は大変良い問題でした。
彼は異なる高さにある２点を考えます。
この２点をＡ，Ｂとし、１点がもう１点の真上にないものとします。
これらの２点を結ぶ直線から円弧、波形に曲がりくねったものまで、
もちろん無数にあるわけです。
そこで、この曲線にそってＡからＢへボールを転がし落とすと想像してみて下さい。
ボールが上の点から下の点にたどり着くまでにかかる時間は当然、
曲線の形に関わってくることになります。
ベルヌーイはボールが最も短い時間で転がり落ちる特定の曲線ＡＢを求めよという問題を出して、
数学界に挑戦したのです。
彼はこの曲線をギリシャ語の“最短”と“時間”という語からとって最速降下問題と呼びました。
明らかに最初に考えつくことはＡとＢを結ぶ直線とすることですが、
ヨハンは軽率な判断を未然に防ぐために言っておこう。
実際Ａ点からＢ点を結ぶ最も短い距離は直線ＡＢであるが、
しかしこれは最も短い時間で動く道ではないのである。
私がその曲線ＡＢに与える名称は幾何学者にはよく知られているものである。
ヨハンは数学界に対し解を受け付ける期限を１６９７年１月１日としました。
しかし期限がきたとき彼は１つの解とともに“敬愛なるライプニッツ”
から手紙を受け取りました。
ライプニッツは期間が短すぎるとの不公平がでないように当分の間この問題は公開し
ておいて、次のイースターまで期限を延ばしたらどうだろう？と丁寧に申し出ました。
さーて、今夜は長ーくなりましたね。
目をこすりながらでもいいですから、最後まで読んで下さい。
皆さんもこの最速降下問題の曲線の名称を考えてください。
答えだけで良いです。
次の夜は本題に入ります。お休みなさい・・・。
NO.466 '99 5/9 水の流れ 最速降下問題（１）
皆さん、NO.415のゼーター関数ζ（２）物語の第１３夜＜特別寄稿＞を思い出してください。
もう一度、ヨハンの考え出した特別問題を書きます。
「異なる高さにある２点を考えます。
この２点をＡ，Ｂとし、１点がもう１点の真上にないものとします。
これらの２点を結ぶ直線から円弧、波形に曲がりくねったものまで、
もちろん無数にあるわけです。
そこで、この曲線にそってＡからＢへボールを転がし落とすと想像して
みて下さい。ボールが上の点から下の点にたどり着くまでにかかる時間は
当然、曲線の形に関わってくることになります。
ベルヌーイはボールが最も短い時間で転がり落ちる
特定の曲線ＡＢを求めよという問題を出して、数学界に挑戦したのです。
彼はこの曲線をギリシャ語の“最短”と“時間”という語からとって
最速降下問題と呼びました。」
ここで、再度、問題を誤解されることがないように、繰り返します。
「与えられた二つの点を結ぶ曲線は無数にありますが、
たとえばその曲線を細い管か溝と考えて、
小さな球をその中に置いて手を放し、
この球が１点からもう１つの点までもっとも短時間に通過する、
そんな曲線を１つあげなさい。」
ヨハンの視界の中にはもっと別な標的がありました。
ヨハンはこう書いています。
「幾何の秘密を見抜いただけでなく、
その分野を拡張したという驚くべき法則を誇っている者たちを含め、
この風変わり問題を解いたという者は現れていない。
ただし、彼らは誰にも知られていないと思っていたらしいが、
その黄金の定理とやらはかなり以前に他の人物によって
発表されていたのである。」
”黄金の定理”とはアイザック・ニュ−トンの発見した流率法をさしています。
ヨハンはこの問題の写しを１６９７年に、
イギリスの造幣局に務めていたニュートンに発送しました。
当時ニュ−トンは姪のキャサリン・コンドウィットと共に
ロンドンに住んでおり、彼女がこのエピソードに触れています。
「１６９７年、その問題がベルヌーイから送られてきたとき、
ニュ−トン卿は貨幣大改鋳で大忙しの最中にあり、
ロンドン塔からはやっと４時に戻ってきた。
たいそう疲れていたが、それを解いてしまうまで（朝の４時だった）、
眠ろうとはしなかった。
アイザック・ニュ−トンは当時もうかなりの年齢になっており、
しかも緊張を強いられる日中の仕事でくたびれていたのに、
ヨーロッパの大多数の者が解決できなかった問題に勝利を収めたのです。
それは偉大なる英国の天才の恐るべき威力を
思い知らせる素晴らしい機会になりました。
この続きは、次回にお送りします。
尚、歴史的事実は、参考文献の「数学の知性」（現代数学社）から、
多くの引用をさせて頂いています。
NO.467 '99 5/10 水の流れ 最速降下問題（２）
ニュートン（イギリス：１６４２〜１７２７）はベルヌーイ兄弟
（スイス兄ヤコブ：１６５４〜１７０５、弟ヨハン：１６６７〜１７４８）や
ライプニッツ（ドイツ：１６４６〜１７２６）が彼の評判や栄光を
打ち砕いてやろうと狙っていることや、
どうせ彼らは自分たちの解を発表してやろうとずうずしながら待ちかまえているに
違いないことをはっきりと感じとっていました。
ですから、ニュートンはこの機会をとらえて、時間が勝負のこの問題をさっさと
解いてしまったのです。多少怒りを込めて彼はこう述べたと言います。
”私は数学上のことで外国人にいじめられるのは好きじゃない”
さてヨーロッパへ戻って、１６９７年のイースター
（キリストの復活を祝う祭り：春分後の最初の満月の次の日曜日）が近づくにつれ、
いくつかの解がヨハンの下に寄せられました。
誰もが探していた・・・（幾何学者ならよく知っている）
・・・曲線は、外でもない上から下へ向かうサイクロイドでした。
この重要な曲線はパスカル（スランス：１６２３〜１６６２）と
ホイヘンス（オランダ：１６２５〜１６９５）によって研究されていましたが、
これが最速降下線にもなることに二人の数学者のどちらも気づいていませんでした。
ヨハンは独特の誇張した言い回しで、
”もし私がこのホイヘンスのサイクロイドこそ求めていた曲線であると言ったら、
あなたがたは驚きのあまり生気を失うであろう”と言っています。
期限であるイースターの日がきました。
ヨハンは合わせて ５つの解を受け取りました。
彼自身のものと、ライプニッツのもの、３つ目が兄ヤコブのもの
（さぞヨハンは落胆したでしょう。解けないと思っていたから）、
ホスピターリ侯爵のものもこれに加わっています。そして、最後が英国の消印のついたものでした。
開封してみると、匿名になっていましたがヨハンはそこに正解を見つけだしました。
彼はアイザック・ニュートンの手強さを思い知らされたのです。
サインこそありませんでしたが、解そのものが迷うことなく天才のサインを示していました。
真実かどうかは怪しいのですが、うれしくなるような伝説が伝えられています。
”私はその爪を見てライオンを識別した”
これで、最速降下線（サイクロイド）にまつわるお話を終わります。
そこで、現代にもどってみます。
東京と大阪を結び最速の乗り物（リニアモターカー）の研究が進んでいますが、
この最速降下線を知っているなら、
是非東京と大阪を結ぶサイクロイドの地下道をつくってもらいたいなー・・・。
また、私自身、興味をもっているのに自然界で、
このサイクロイドの性質を使っている乗り物を見つけたいです。
例えば、ジェットコウスターとか、奈良の東大寺の屋根の優雅な曲線は
雨が自然に早く落ちるように設計されていて、このサイクロイド曲線がモデルかなー・・・。
もし、ご存じ方があれば、お知らせください。
尚、遅くなりましたが、いつものように、
歴史的事実は、参考文献の「数学の知性」（現代数学社）から、多くの引用をさせて頂いています。
| NO.468 | '99 5/10 | Junko | 最速降下問題（３） |
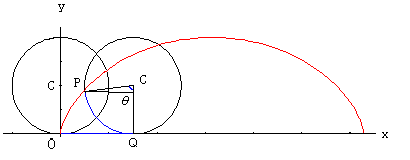
最速降下問題の答えでもある、サイクロイド曲線についてかきます。
右の図のように、直線上を円が転がるときに、
円周上の定点Ｐが動く軌跡をサイクロイドと呼びます。
この円の半径をａ、∠PCQをθとすると、
点Ｐ(x,y)は次の様に表示されます。
線分OQ=弧PQであることに注意して、
x=a(θ-sinθ)
y=a(1-cosθ)
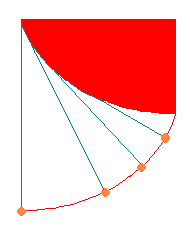
| NO.476 | '99 5/15 | プ−太 | 最速降下問題 （４） |
サイクロイドが使われている例として、振り子がありますよ。
図@最速降下曲線において、曲線の途中から玉を離しても、
てっぺんから玉を離したのと同時にゴールへたどりつきます。
つまり、曲線のどこから玉を離しても、ゴールへたどりつく時間は同じになります。
（最速降下曲線自身を求めるのは、変分法などを用いて、
図@の主張は微積分を用いて、説明できます）
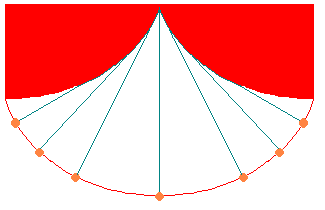
図Aサイクロイド自身の伸開線は同じくサイクロイドになります。
つまり、サイクロイドに糸を巻きつけて、
図Aの下の端をもって糸をピンとはったままはがしていくと、
糸の端の描く曲線はサイクロイドになります。
（ここら辺は、微分幾何の曲線論です）
図Bそういった性質をつかっていつも同じ周期で振れる振り子がつくれます。
これを等時性といいます。
普通の（軌跡が円である）振り子も等時性をもつのですが、
厳密には違います。
高校物理で、普通の振り子の周期は素材が糸であるか棒であるかにとって
違うが、振り子の長さによってのみ周期が決まる（振れ幅には関係しない）
習った人がいるかもしれません。
しかし、それは振れ幅が小さいときには、
sinθ＝θと近似的表わされるとして周期を計算したのです。
（これを厳密にやると、周期は楕円積分で表わされるそうです。）
図Bの振り子は、サイクロイド型の天井に糸でできた振り子を揺らし、
振り子の軌跡をサイクロイドにしようとしたものです。
振れ幅が大きくても、また減衰して小さくなっても、
理論的には完全に同じ周期でゆれます。
ただ、現実的には、天井のサイクロイドに巻き付いている影響は少なく、
ほとんど無意味みたいです。
なかなか面白いとおもいませんか？
| NO.1147 | 2002.2.1. | 遊未 | 最速降下問題 （５） |
NO.476 最速降下問題の、図@での最速降下曲線自身を求める式、
どこから離してもゴールにたどりつく時間は同じという主張の証明を、
詳しく知りたいです。
どなたかおねがいします。
| NO.1150 | 2002.2.3. | yokodon | 最速降下問題 （６） |
この問題を解くのに必要な知識は、以下です。
質量 m の物体が、ある曲線 y ＝ f(x) の形状をした滑らかな“斜面”にそって２
次元運動し、摩擦はなく重力のみを外力として受けるものとして考えます。物体の初
速度は、（0,0）とします。
物体の力学的エネルギー保存則は、以上の仮定の下で次式になります。
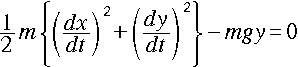・・・[1]
[1] 式を、以下のように書き換えます。２乗の扱いですが、複号の正を取ることに
します。
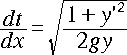・・・[2]
これを、積分します。
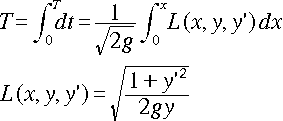
・・・[3]
都合上、右辺の被積分関数を L(x,y,y')と置いています。
さて、この T を最小にするような y = f(x) を求めるわけです。 ここで変分法を使います。「関数 f(x) を“変化”させたときの、T の最小値」を 求めるのが、変分法です。些か数学的な正確さを犠牲にして議論を進めますが、関数 y の任意の“微小変化”を δu とし、このときの T の“変化”をδT とすると、部 分積分から、以下のように変形できます。
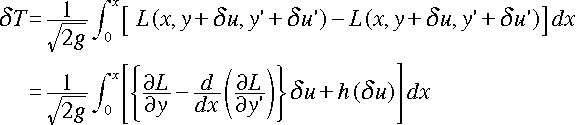
（ h(p) は、p の２次以上の整式）
ここで、δu は任意でしたから、δT ＝ 0 となる条件下では、
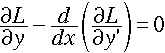・・・[4]
が成り立ちます。これが、『オイラー・ラグランジュ方程式』と
呼ばれるものです。
本問の条件に戻って、[4] を計算すると、整理して最終的に以下のようになります
（途中は、長いので省略しています）。
y'2 + 2yy'' + 1 ＝ 0 ・・・[5]
これを解くと、サイクロイドの曲線の式が出てきます
両辺に y' をかけると、d/dx{yy'2 + y} ＝ 0 となり、x で積分すると、
y' = {(A2-y)/y}1/2 ・・・[6]
という形に出来る（A：積分定数）ので、そこで置換積分をします。
[6] 式で、y ＝ A2・sin2(u/2) とおくと、結局以下の結果を得ます。
x ＝ A2/2・(u - cos(u)) , y ＝ A2/2・(1 - sin(u))
この解の結果から、[3] の値が（x,y の初期値と終点に依存した）定数になること
は、[3] に解を代入して置換積分を実行すると出てきます。
| NO.1152 | 2002.2.9. | 遊未 | 最速降下問題 （７） |
NO.1150 最速降下問題（６）
への質問なんですが、
[1]から[2]への書き換えと、[5]からどうすればサイクロイドの式が出るのか、
そこの部分が考えたんですが、よく分かりません。
できるなら詳しい式を示していただきたいのですが…
| NO.1153 | 2002.2.9. | yokodon | 最速降下問題 （８） |
[1] → [2] の変形と、[5] からサイクロイドの式への変形について、やりかたを
お示ししたいと思います。
（1）[1] → [2] の変形
まず、次の事実に着目します（合成関数の微分）。
dy/dt ＝ dy/dx・dx/dt
これを [1] 式に代入し、整理します。
1/2・m・{1 + (dy/dx)2}・(dx/dt)2 - mgy ＝ 0
これを、dx/dt について、解いてみて下さい。
さて、dt/dx ＝ 1/(dx/dt) ですから、以上から [2] を得ます。
（2）[5] →サイクロイド解
[5] 式の両辺に y' (＝ dy/dx) を掛けます。
y'3 + 2yy'y'' + y' ＝ 0 ・・・[7]
ところで、
d/dx(y・y'2) ＝ y'3 + 2yy'y''
ですから、微分の線形性から、[7] 式は結局、
d/dx{y・y'2 + y} ＝ 0 ・・・[8]
と同値です。y ≧ 0 に注意して、A2 （A：ある実数）を積分定数として、[8] 式の
積分は
y・y'2 + y ＝ A2
となります。これを y'（＝ dy/dx）について解いたものが [6] 式です。復号の正を
採りました。
y' = {(A2-y)/y}1/2 ・・・[6]
[6] 式は、変数分離型の微分方程式なので、
∫{y/(A2-y)}1/2 dy=∫dx
と、変形できます。この左辺で、以下の変数変換をします。
y ＝ A2・sin2(u/2)
これで置換積分をすると、最終的な結果になります（No.1150の結果には、積分定
数が A しか出てきていませんが、初期時刻にて（x,y）＝（0,0）であることを暗に
使いました）。
| NO.1158 | 2002.2.20. | ＤＤＴ | 最速降下問題 （９） |
最速降下線の途中から重りを離しても、その運動周期は離した位置に無関係なことを示します。
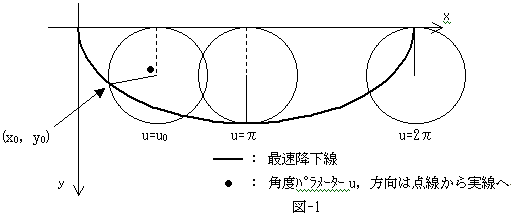
まずNO.1150の結果（2/9修正版）より、運動は上図の曲線上に束縛される1次元運動です。
重りの軌道の束縛曲線である最速降下線を、ﾊﾟﾗﾒｰﾀuを用いて書けば、
x＝a(u−sin u)
y＝a(1−cos u) (1)
です。ただしA2/2をaとしました。aは図-1の円の半径です。
まず、最速降下線の1点（x0(u0)，y0(u0)）から落下する重りが、
同じ曲線上の別の点（x(u)，y(u)）に達するまでの経過時間を運動方程式を解いて求める方法は、
uに対する運動方程式が複雑で諦めました。
そこで問題を解かずに経過時間のみ求める方法をご紹介します。
この方法は、NO.1150の[3]で適用な置換積分を実行するのと同等です。
どちらもエネルギー保存則をdt/dxについて解いて、xで積分し経過時間を求めます。
重りの運動はuに関する1次元運動とみなせるので、典型的な1次元運動を考えます。
運動を表す座標をx，速度v＝dx/dtとするとエネルギー保存則は、
E＝T＋U＝1/2･mv2＋U(x) (2)
と書けます。ここでmは粒子の質量，TはT＝1/2･mv2で運動エネルギー，
U＝U(x)は保存力を導く力のポテンシャルです。
(2)を運動量pと座標xで書きかえるために、突然ですがラグラジアンなるものを考えます。
L＝T−U＝1/2･mv2−U(x) (3)
がラグラジアンです。L＝L(v，x)と考えてLをVで偏微分すると、運動量の表式が得られます。
∂Ｌ/∂v＝mv (4)
ここで運動量をpとし、p＝mvを用いて(2)からvを消去すると、
E＝1/2m･p2＋U(x) (5)
となります。運動量と座標で表されたエネルギーの表式をハミルトニアンと呼び、
ふつうE＝H(p，x)で表します。ハミルトニアンからは、運動方程式を導けます。
∂H/∂p＝ dx/dt (6)
∂H/∂x＝−dp/dt (7)
とおくと、通常の運動方程式m･d2x/dt2＝−U(x)が得られます。
通常の座標や運動量を用いた場合、これらはトリビアルな結果ですが、
式(1)を用いた時のように任意に変換された座標に対しても、
関係(4)，(6)，(7)はそのままの形で成り立つので、その場合はトリビアルではありません。
以下の関係は、1次元運動を表す任意の座標qに対して成立します。
運動量pは式(4)から、p＝∂Ｌ/∂vとして得られるものです。
作用変数Iを不定積分、
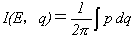(8)
で定義します。作用変数Iの物理的意味は、一般化角運動量とでも言うべきものですが、
とても説明しきれないので省略します。
I＝I(E，q)なのは、エネルギー保存則Ｅ＝Ｈ(p，q)より、p＝p(E，q)であるためです。
∂I/∂Eを計算します。積分記号下の微分を利用して、
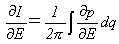(9)
と書けます。またＥ＝Ｈ(p(E，q)，q)より、
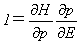
となり、
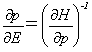
が成り立ちます。ところが（p，q）に関する式(6)の関係が、
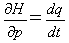
であるために、作用変数IのエネルギーEに関する微分は、
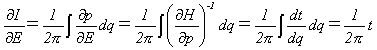(10)
であることがわかります。よって式(10)により、運動が開始されてからの経過時間tを計算できます。
この積分を周期運動の１周期に関して行えば、明らか運動の周期が出ます。
しかも作用変数Iの定義(8)を見るばわかるように、
I(E，q)を計算するためには、p＝p(E，q)の形がわかれば良いので、
エネルギー保存則の表式Ｅ＝Ｈ(p，q)が必要なだけです。
従って実際にq＝q(t)の形を具体的に求めなくても周期を計算でき、
しかも任意の座標で同じ方法が使えます。
今の場合、座標uに関する力学的エネルギーを計算してみると、･ を時間に関する微分として、
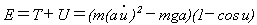(11)
となります。しかし式(11)にはまだ、計算に関して面倒を起こしそうな超越関数(1−cos u)が
含まれています。三角関数がいくら初等超越関数であろうと超越関数は超越関数です。
もう一度変数変換して、必ず求積可能で、ある程度は代数処理も可能な有理関数への帰着を試みます。
q=1-cosu (12)
とおけば、
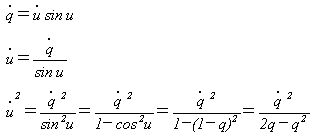
なので、
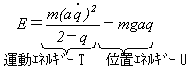(13)
が得られます。ラグラジアンLは、式(13)の位置エネルギーの符号を変えたものなので、
座標qに対する運動量pは、
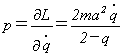(14)
で定義されます。これを式(13)に代入すれば、
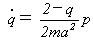
なので、
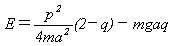(15)
となります。目的は(p，q)に関する作用変数Iの、
エネルギーEに関する微分∂I/∂Eを計算することですが、
位相空間{(p，q)}で運動を表すと、より計算に便利な幾何学的意味を作用変数Iに
与えられます。そのために式(15)をqについて解きます。
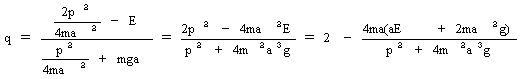(16)
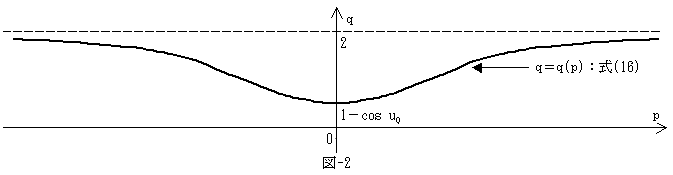
と変形できるので、運動の軌跡は図-2となります。
ここでエネルギーEは図-1と式(11)から、
E(u0)=-mga(1-cosu0) (17)
です。また作用変数Iの定義式(8)の積分∫p･dqは、
図-2のq＝2と式(16)の曲線の間に挟まれた面積です。
面積なので、q＝2と式(16)のq＝q(p)を使って直接pで積分しても同じです。
積分範囲は、図-1からu0≦u≦2π−u0なので、p，qの定義式(12)，(14)をたどることにより、
uに関する運動の1周期、
u＝u0 → π → 2π−u0 → π → u0
に対して、
cos u＝cos u0 → -1 → cos u0 → -1 → cos u0
q＝1−cos u
＝1−cos u0 → 2 → 1−cos u0 → 2 → 1−cos u0
で、qの増減と図-2の曲線の概形（漸近線はq＝2）、およびp＝2ma2/(2−q)･dq/dtから、
p＝0 → ＋∞ → −∞ → 0 → ＋∞ → −∞ → 0
となります。すなわち図-2のq＝2とq＝q(p)が無限遠でつながった閉曲線と考えて、
状態点(p，q)は、uに関する運動の1周期の間に、閉曲線を2周します。
従ってuの1周期に対応する作用変数は、式(16)が偶関数なのを考慮して、
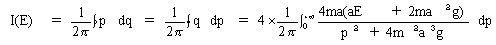(18)
と書けます。ところでいま欲しいのは、式(18)の積分値ではなく、
そのEに関する微分です。不定積分による定義(9)に従い、
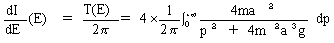(19)
が得られます。ここで式(19)のT(E)は、運動の周期Tが、
重りの持っている力学的エネルギーEの関数であるかもしれないと言ってます。
力学的エネルギーEは式(17)より、重りの初期位置u0の関数です。
いいかえれば運動の周期TがEに影響されるということは、
重りの初期位置u0に影響されることになります。
式(19)の最右辺の積分はEを含まないので、運動の周期TはエネルギーEに影響されません。
従って最速降下線振り子の等時性が示せました。これが最初の目的です。
最初に述べたようにこの方法は、
NO.1150の[3]の積分を実行するのと本質的に同等ですが、
力学問題という制約条件があるために作用変数を導入すると、
正しい置換のやり方をほぼ自動的に示してくれるのだと思います。
| NO.1159 | 2002.2.20. | Akira | 最速降下問題（１０） |
最速降下問題について。どの位置から落下させても同じ時間で下に辿り着く、
ということの証明の方法と、証明中の式を細かくしりたいんです…。
大学の授業でやったけど、間の計算や式、細かい証明方法が理解できなくて困ってます。
| NO.1160 | 2002.2.24. | yokodon | 最速降下問題（11） |
到達時間に関して
サイクロイド解から、所要時間を求める部分をご説明します。
等時性に関する詳しい説明は、DDT さんが既に丁寧にして下さっているので、省略
致します。
NO.1150の [3] 式に、以下を代入します。
x ＝ A2/2・(u - sin(u)) , y ＝ A2/2・(1 - cos(u))
ところで、
dx/du ＝ A2/2・(1 - cos(u)) , dy/du ＝ A2/2・sin(u)
ですから、
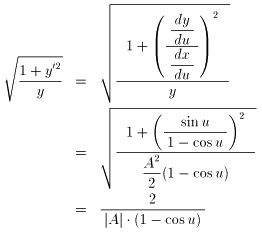
となります（途中は、省略しました）。
よって、[3] 式から、t ＝ T のとき u ＝u1 であるとすると、
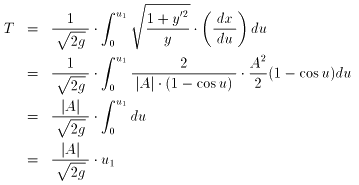
のようになります。
さて、A と u1 は、共に曲線の概形を決めるパラメータ（前者は初期条件のもと
で決まる積分定数、後者は境界条件の一つ）でした。一方、T と u1 の関係に関し
て見方を変えれば、u を t の関数としてみたとき、u(0) ＝ 0 とすれば、
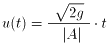
となることが分かります。
戻る