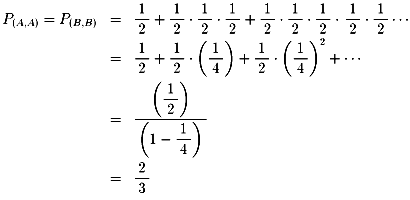
4.従って、相手にサ−ブ権がある状態で自分が得点する確率 P(A,B)=P(B,A)は、
Weekend Mathematics/コロキウム室/1999.4〜6/NO.62
| NO.526 | '99 6/8 | Junko | バーレーボールの得点(3) |
3.自分にサ−ブ権がある状態で自分が得点する確率 P(A,A)=P(B,B)を求めます。
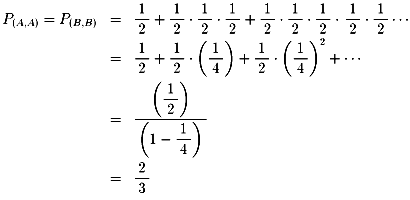
4.従って、相手にサ−ブ権がある状態で自分が得点する確率
P(A,B)=P(B,A)は、
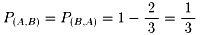
どちらが得点したかで場合分けしていきます。
その時に、どちらにサ−ブ権があるか気をつける必要があります。
また、得点に関係しないサ−ブ権の移動は考えなくてもいいことにご注意ください。
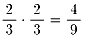
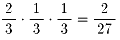
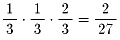
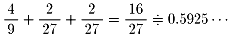
5.
同様にどちらのチ−ムが得点したかで場合わけです。
(相手チ−ムが得点した後に得点するような場合を赤で表示しています。)
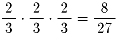
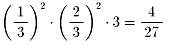
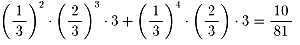
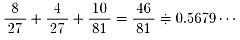
サ−ブ権を持って試合を開始したチ−ムの方が、
最初は有利(最初の1点は2/3と1/3)ですがだんだんとその度合いが弱くなり、
15点ともなるとほとんど気にならない程度(1/2と1/2)になるのでしょうか?
でも、15点まで検証するのはちょっと大変そう?

| NO.527 | '99 6/9 | 水の流れ | 置換積分(12) |
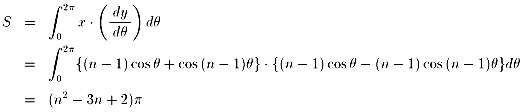
さらに、n=3のとき、特にデルトイド、
n=4のとき、特にアステロイド と言います。
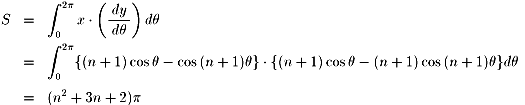
さらに、n=1のとき、カージオイド(心臓形)、
n=2のとき、ネフロイド(腎臓形)と言います

| NO.528 | '99 6/12 | Idaho Potato | 連続の証明(7) |

| x - a | < δは、 0 < | x - a | < δが正当。
なぜなら、x = a を除外しておかないと、
f(a) = αを含意することになり、結果的に、
「極限の定義」ではなく、「連続性の定義」になってしまいます。
NO.524
証明の3行目以下での δ の選び方:
「そのような δ は必ず存在する」で済ませても
よいかもしれませんが、たとえば、次のようにすれば、
δを具体的に選び出すことができます。
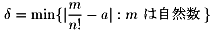
右辺の値が存在して、しかも 0 でないことは、
a が無理数であることからわかります。

| NO.529 | '99 6/12 | Idaho Potato | 連続の証明(8) |
No.524でJunkoさんが 「連続の証明」を完結してくれたところで、 ε-δの意味や背景について、少し考えてみましょう。
「関数が連続である」という言葉から、
どのような状態を想像しますか?
たいていの人は、その関数のグラフを考えて、
「グラフの線がつながっている」というイメージでとらえると思います。
その「イメージ」をもう少し明確にするためにつくられたのが、
「関数の極限」という概念を用いた連続性の定義です。
それでは、「関数の極限」とは何でしょうか?
高校の教科書では、「極限」に対する素朴なイメージを、
「限りなく近づく」などという表現で説明しています。
しかし、このような直観的な説明だけでは、
極限の概念を数学の対象として扱うためには不十分です。
そこで、数学的に厳密で曖昧性のない形で、
「限りなく近づく」ということの意味を明確にするために考え出されたのが、
ε-δを用いた極限の定義なのです。
そして、ε-δによって厳密に定義された極限の概念を用いることによって、 関数の連続性も、数学的に厳密に定義されるのです。
ところで、こうして定義された「関数の連続性」というのは、
私たちが持っている「連続な関数」に対する直観的なイメージを正しく反映しているのでしょうか?
No.511の問題は、
まさにこのようなことを私たちに問いかけていると思います。
「連続 = グラフの線がつながっている」という立場で考えると、
No.511の関数は、そもそもグラフを描くこと自体が困難(不可能?)ですし、
想像力をたくましくしてグラフを思い浮かべてみても、
それは、とても「線がつながっている」などと形容できるものではありません。
ところが、ε-δによって定義された「連続性」の概念というのは、
このような、一見「連続」とは思えないような関数をも含んでしまうのです。
ε-δによる連続性の定義というのは、
「連続性の概念を厳密に定めて、
数学の対象として扱えるようにする」という数学的な要求は、
確かに満たしています。
しかし、
「関数が連続であるとはどういうことか」という「哲学的」な問いに対しては、
必ずしも十分な答えを与えているわけではないように思えます。

| NO.530 | '99 6/12 | 水の流れ | 高貴な未解決問題・その2 |
第2話:「完全数」
自然数の正の約数について、考えてみましょう。
例えば、6の約数は6=2×3より、1,2,3,6です。
これらを足してみると、1+2+3+6=12となり、
ちょうど元の6の2倍になっています。
このように、自然数nの正の約数の和が元の自然数の2倍になっているような
数を完全数と言います。
これは、ピュタゴラス学派(紀元前500〜300年)が自然数の素因数分解の中で、
発見していったと思われます。
この定義から、最初のいくつかの完全数は、6,28,496,8128,… であることが割
合早くから知られています。
6=3×2=(1+2+3+6)×2
28=7×4=(1+2+4+7+14+28)×2
496=31×16=(1+2+4+8+16+31+62+124+248+496)×2
…………
ここで、数字P=q×2(p−1)<qは素数>であるが完全数を考えてみます。
2とqは素数だから、Pは素因数分解されています。
qの約数の和は1+q
2(p−1)の約数の和は1+2+4+…+2(p−1)=2p−1であり、
P=q×2(p−1)の約数の和は、掛けてみると、(q+1)(2p−1)
一方、Pは完全数だから、Pの約数の和は 2×q×2(p−1)=q×2p
両者が等しいことより、 (q+1)(2p−1)=q×2p
展開して、比べると、q=2p−1
それで、qが素数なら、
q×2(p−1)=(2p−1)・2(p−1)
そして、 M(p)=2(p−1)がメルセンヌ数で、素数なら
P=(2p−1)・2(p−1) は完全数になります。
現在までに、分かっている完全数を順に、書きます。
6(p=2)、28(p=3)、496(p=5)、8128(p=7)、
33550336(p=13)、
8589869056(p=17)、137438691328(p=19)、
2305843008139954128(p=31)
……
そして、今現在の最大の完全数はP=2859433×(2859433−1)
という気の遠くなるような大きな数字です。
さて、完全数の「オイラーの定理」を書く前に、この偉大で有名な数学者を紹介します。
スイスの数学者のオイラーは(Leonhard Euler,1707〜1783)
ヨハン・ベルヌイーにより指導され、ペテルスブルクのアカデミーとベルリンの科学アカデミー
で仕事をした。彼は驚くべき記憶力の持ち主で、1735年に右目の視力を失ったし、また、
1766年には左目の視力も無くした。それにもかかわらず、彼は驚くべき記憶力の助けで、
口述をさせることにより、彼の研究成果を発表し続けたのである。オイラーは最も卓越した数学の
著作家で、13人の子供がいたが、生涯に800以上の論文を書いた。
また、パリのアカデミーから12回も賞を受けている。
フランソア・アラゴは、次のように述べている。
「オイラーは人が息をするように、鷲が空中にいるように計算をした」と。
オイラーは記号、e,i やxの関数f(x)の記号を導入することにより、数学を系統的にした。
彼は、微分方程式に偉大な貢献をした。
「無限小解析入門」(1748年)は解析学の基礎を与えた。
オイラーは、ベーター関数やガンマー関数、またゼーター関数をも研究した。
フランスの有名なラプラスは「オイラーを読め、オイラーを読め、彼は万物について私達の師匠である」
と学生たちに言ったそうである。
お待たせしました。
「オイラーの定理」:
nが(2p−1)・2(p−1)の形を持ち、
2p−1が素数なら、そのときに限りnは偶の完全数である。
<証明> 条件が十分であることは、前に述べてあるので、分かりますから、次に必要であることを
示してください。皆さん!考えてください。
皆さんは、21世紀には(今世紀中かも)何番目かの完全数数を見ることができるでしょう。 是非、チャレンジください。完全数数は話題がつきません。
そこで、問題です。
問題:完全数のすべての約数の逆数の和は2であることを証明してください。
<参考文献:素数の不思議:好田順治著(現代数学社)>

| NO.531 | '99 6/14 | 水の流れ | 本を棚に入れる問題(1) |
太郎さんは作業机の下にいっぱいの本があります。
一度、整理して本棚に入れたいと思っています。
入れ方にもいろいろな場合があることに太郎さんは気がつきました。
<1> 本でみると、異なる本なのか、見分けのつかない本なのかが問題になります。
<2> 本棚においても同じことで、異なる棚か、同じ棚かを考えなければなりません。
これで、この組み合わせによって、4つの場合に分かれます。まだあります。
<3>どの本棚にも必ず本を入れて空がないように入れるか、それとも本をいれない棚を
許すかにもよります。
結局8つの場合を考えて、整理することにしました。
問題1:5冊の異なる本を、3個の異なる棚に入れる方法は何通りでしょうか?
ただし、空の本棚があっても良いとする。
問題A:一般に、m冊の異なる本を、n個の異なる棚に入れる方法は何通りでしょうか?
ただし、空の本棚があっても良いとする。
問題2:5冊の異なる本を、3個の異なる棚に入れる方法は何通りでしょうか?
ただし、空の本棚があってはいけないとする。
問題B: 一般に、m冊の異なる本を、n個の異なる棚に入れる方法は何通りでしょうか?
ただし、空の本棚があってはいけないとし、m≧nとする。
問題3:5冊の同じ本を、3個の異なる棚に入れる方法は何通りでしょうか?
ただし、空の本棚があっても良いとする。
問題C:m冊の同じ本を、n個の異なる棚に入れる方法は何通りでしょうか?
ただし、空の本棚があっても良いとする。
問題4:5冊の同じ本を、3個の異なる棚に入れる方法は何通りでしょうか?
ただし、空の本棚があってはいけないとする。
問題D:m冊の同じ本を、n個の異なる棚に入れる方法は何通りでしょうか?
ただし、空の本棚があってはいけないとし、m≧nとする。
太郎さんは本の整理に疲れてきましたので、後半の入れ方は次回にしたいと思っています。

| NO.532 | '99 6/15 | Junko | 本を棚に入れる問題(2) |
B(5,1)=1
B(5,2)=25−{2C1・B(5,1)}=32−2=30
B(5,3)=35−{3C1・B(5,1)+3C2・B(5,2)}=243−93=150
B(5,4)=45−{4C1・B(5,1)+4C2・B(5,2)+4C3・B(5,3)}=1024−784=240
B(5,5)=55−{5C1・B(5,1)+5C2・B(5,2)+5C3・B(5,3)+5C4・B(5,4)}=3125−3005=120
・・・
nHm=n+m−1Cmについて
先程の例(3H5)でいえば、
5冊の本を、(3−1)=2つの仕切りで仕切ると考えます。
《BBB|B|B》・・・1つ目の本棚に3冊、2つ目の本棚に1冊、3つ目の本棚に1冊
《BB||BBB》・・・1つ目の本棚に2冊、2つ目の本棚はなし、3つ目の本棚に3冊
といった具合です。
これは、本5+仕切り2=7個のものを並べる並べ方、ただし本、仕切りともそれぞれ区別はしない
ということで、7C5(または、7C2)となります。
一般にnHmの場合には、n個のものと、m−1個の仕切りを1列に並べると思えばいいので、
n+m−1Cmになるわけです。

| NO.533 | '99 6/15 | 月の光 | タイル敷き(3) |
この問題は始め、2重積分や複素数や難しい数学を使って証明されました。
これはちょうどネズミを殺すのに大砲を持ってくるようなものだそうです。
1985年に数学者のモントゴメリーはある会議においてもっと初等的な証明をしようと提案しました。
その後この提案に応えて13の異なる証明が出されました。
そのうち、最も簡単な証明の一つであるリチャード・ロッホバーグの証明を紹介します。
証明)
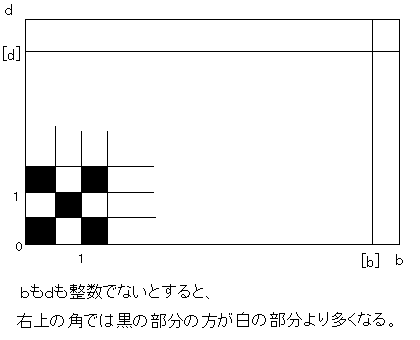
大きい長方形を、左下の角を基点として単位長さの半分を一辺とする正方形のチェッカー盤パターンに
分ける。それぞれのタイルには整数の辺があるから、黒と白が同じ面積あるはずである。
このようなタイルが大きな長方形を完全に覆うとすると、大きい方も黒と白が同じ面積あることになる。
したがって大きい長方形の少なくとも一つの辺は整数の長さになる。
もしそうでないとすると、大きい長方形は4つの部分に分割され、そのうちの3つの部分は黒と白が同じ
面積あるが、4番目の部分はそうでないことになる。
証明終)
この他の証明には正方形を数えるいろいろな方法、素数や多項式、ステップ関数、グラフ理論を用いるもの
などがあります。
<引用:現代数学ミステリーツアー(新曜社)>

| NO.534 | '99 6/16 | 月の光 | 連続の証明(9) |
NO.516連続の証明(4)の証明で、
|x2-4|=|(x+2)(x-2)|<|x+2||x-2|とありますが、
ここは”=”ではないでしょうか?
また、δ<min(ε/8 ,√ε/2)の意味を教えて下さい。

| NO.535 | '99 6/16 | 水の流れ | サッカーのリーグ戦 |
今、サッカーのシドニーオリンピックアジア地区1次予選が行われています。
日本は5カ国のリーグ戦を戦っています。
では、引き分けはないとして、起こりうる勝敗の順位表は何通りでしょう。
ちなみに、3カ国のリーグ戦の場合は2勝、1勝1敗、2敗
3チームとも1勝1敗 の2通りです。
そこで、順にチーム数増やしていきます。
4チームの場合は何通りでしょう?
6チームの場合はと考えていきます。
太郎さんは、現在の段階では地道に数えてみることにしました。

 E-mail
E-mail
 戻る
戻る