Weekend Mathematics乛僐儘僉僂儉幒乛1999.4乣6乛NO.56
| NO.474 | '99 5/15 | 悈偺棳傟 | 塅拡嬻娫偱偺嵟抁宱楬栤戣乮俋乯 |

僐儘僉僂儉幒NO.313乽塅拡嬻娫偱偺嵟抁宱楬栤戣乿偺夝愢傪偟傑偡丅
傑偢偼丄NO.399傪尒偰偔偩偝偄丅偙偙偱丄僔儏僞僀僫乕偺僱僢僩儚乕僋偐傜丄
佢俢俙俵亖俁侽並偵側偭偰偄傑偡丅
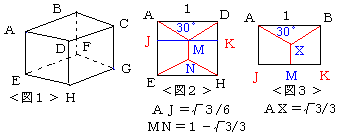
恾俀傪嶲徠偟傑偟傚偆丅
偙偺応崌侾曈偺挿偝傪侾偲偟偰偁傝傑偡丅

偟偨偑偭偰丄塅拡嬻娫偵偍偗傞俉偮偺尋媶巤愝傪寢傇嵟抁宱楬偺挿偝偼侾曈偑侾侽倣偱偡偐傜丄俇侾丏俋俇倣偱寢偽傟傑偡丅
偲偙傠偱丄懢榊偝傫偼愝寁恾偑偆傑偔彂偗側偔偰崲偭偰偄傑偡丅
偙傟傑偱偺僀儊乕僕傪嶲峫偵偟偰丄奆偝傫峫偊偰偔偩偝偄丅

| NO.475 | '99 5/15 | 悈偺棳傟 | 棫曽懱偺揥奐乮俀乯 |
僐儘僉僂儉幒NO.314乽棫曽懱偺揥奐恾乿偺夝愢傪偟傑偡丅
俇偮偺惓曽宍偐傜側傞晛捠偺揥奐恾偼侾侾捠傝偁傝傑偡偑丄
偡傋偰愗傝奐偄偨廃偺挿偝偺崌寁偼俈侽們倣偵側傝傑偡丅
偦偙偱丄愗抐偡傞挿偝偑俈侽們倣傛傝抁偄曽朄傪弴偵懢榊偝傫偼峫偊傑偟偨丅
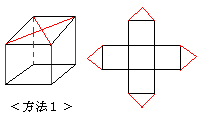
亙曽朄侾亜棫曽懱偺忋柺傪俀偮偺懳妏慄偵増偭偰愗傞応崌偱偡丅
愗抐偡傞挿偝偼係侽亄俀侽併俀佮俇俉丏俁們倣丂偵側傝傑偡丅
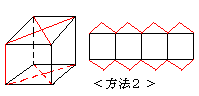
亙曽朄俀亜棫曽懱偺忋柺偲壓柺偺懳妏慄偲偦偺俀偮偺柺傪寢傇曈傪愗傞応崌偱偡丅
愗抐偡傞挿偝偼侾侽亄係侽併俀佮俇俇丏俇們倣丂偵側傝偝傜偵抁偔側傝傑偡丅
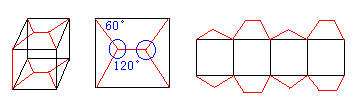
亙曽朄俁亜棫曽懱偺忋柺偲壓柺偵僔儏僞僀僫乕偺僱僢僩儚乕僋傪巊偄傑偡丅
偙偺僔儏僞僀僫乕偺僱僢僩儚乕僋偼NO.393傪嶲徠偟偰偔偩偝偄丅
愗抐偡傞挿偝偼俁侽亄俀侽併俁佮俇係丏俇們倣丂偵偟偐側傝傑偣傫丅
偙傟偑嵟傕抁偄愗抐曽朄偱偡丅
彯丄僔儏僞僀僫乕乮侾俈俋俇乣侾俉俇俁乯偼値屄偺揰傪寢傃
嵟抁僱僢僩儚乕僋傪峫偊偨偙偱抦傜傟偰偄傑偡丅

| NO.476 | '99 5/15 | 僾亅懢 | 嵟懍崀壓栤戣 乮係乯 |

僒僀僋儘僀僪偑巊傢傟偰偄傞椺偲偟偰丄怳傝巕偑偁傝傑偡傛丅
恾嘆嵟懍崀壓嬋慄偵偍偄偰丄嬋慄偺搑拞偐傜嬍傪棧偟偰傕丄
偰偭傌傫偐傜嬍傪棧偟偨偺偲摨帪偵僑乕儖傊偨偳傝偮偒傑偡丅
偮傑傝丄嬋慄偺偳偙偐傜嬍傪棧偟偰傕丄僑乕儖傊偨偳傝偮偔帪娫偼摨偠偵側傝傑偡丅
乮嵟懍崀壓嬋慄帺恎傪媮傔傞偺偼丄曄暘朄側偳傪梡偄偰丄
恾嘆偺庡挘偼旝愊暘傪梡偄偰丄愢柧偱偒傑偡乯
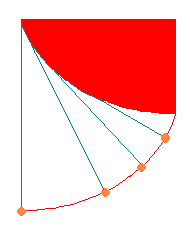
恾嘇僒僀僋儘僀僪帺恎偺怢奐慄偼摨偠偔僒僀僋儘僀僪偵側傝傑偡丅
偮傑傝丄僒僀僋儘僀僪偵巺傪姫偒偮偗偰丄
恾嘇偺壓偺抂傪傕偭偰巺傪僺儞偲偼偭偨傑傑偼偑偟偰偄偔偲丄
巺偺抂偺昤偔嬋慄偼僒僀僋儘僀僪偵側傝傑偡丅
乮偙偙傜曈偼丄旝暘婔壗偺嬋慄榑偱偡乯
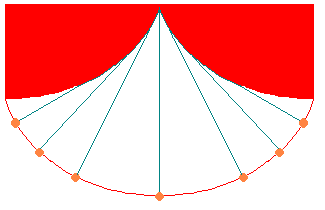
恾嘊偦偆偄偭偨惈幙傪偮偐偭偰偄偮傕摨偠廃婜偱怳傟傞怳傝巕偑偮偔傟傑偡丅
偙傟傪摍帪惈偲偄偄傑偡丅
晛捠偺乮婳愓偑墌偱偁傞乯怳傝巕傕摍帪惈傪傕偮偺偱偡偑丄
尩枾偵偼堘偄傑偡丅
崅峑暔棟偱丄晛捠偺怳傝巕偺廃婜偼慺嵽偑巺偱偁傞偐朹偱偁傞偐偵偲偭偰
堘偆偑丄怳傝巕偺挿偝偵傛偭偰偺傒廃婜偑寛傑傞乮怳傟暆偵偼娭學偟側偄乯
廗偭偨恖偑偄傞偐傕偟傟傑偣傫丅
偟偐偟丄偦傟偼怳傟暆偑彫偝偄偲偒偵偼丄
sin兤亖兤偲嬤帡揑昞傢偝傟傞偲偟偰廃婜傪寁嶼偟偨偺偱偡丅
乮偙傟傪尩枾偵傗傞偲丄廃婜偼懭墌愊暘偱昞傢偝傟傞偦偆偱偡丅乯
恾嘊偺怳傝巕偼丄僒僀僋儘僀僪宆偺揤堜偵巺偱偱偒偨怳傝巕傪梙傜偟丄
怳傝巕偺婳愓傪僒僀僋儘僀僪偵偟傛偆偲偟偨傕偺偱偡丅
怳傟暆偑戝偒偔偰傕丄傑偨尭悐偟偰彫偝偔側偭偰傕丄
棟榑揑偵偼姰慡偵摨偠廃婜偱備傟傑偡丅
偨偩丄尰幚揑偵偼丄揤堜偺僒僀僋儘僀僪偵姫偒晅偄偰偄傞塭嬁偼彮側偔丄
傎偲傫偳柍堄枴傒偨偄偱偡丅
側偐側偐柺敀偄偲偍傕偄傑偣傫偐丠

| NO.477 | '99 5/17 | 悈偺棳傟 | 僆僀儔乕偺乽柍尷夝愅擖栧乮侾乯乿乮俋乯 |
僆僀儔乕偺乽柍尷夝愅擖栧乮侾乯乿偺戞俆栭偺巒傑傝丄巒傑傝丅
師偺摍幃偑婎杮偱偟偨偹丅

偙傟傜偺抣偼僛乕僞乕偺摿庩抣偲偟偰偺夝庍偑偱偒傑偡偟丄
帺慠奅偵傕晛捠偵昞傟偰偄傞偐傕偟傟傑偣傫丅
偨偲偊偽丄儔儌儘乕偝傫偼侾俋俋俈擭偵丄検巕椡妛偵偍偄偰俆侽擭娫
擮婅偲偝傟偰偒偨僇僔儈乕儖岠壥傪傾儊儕僇偺僔傾僩儖偵偍偗傞幚尡偱
妋擣偟偨偲偒偺棟榑抣偼幚幙揑偵
侾亄俉亄俀俈亄俇係亄丒丒丒亖侾乛侾俀侽丂丂偱偟偨丅
柍尷戝偵側傞偲偙傠傪偆傑偔堷偒嫀偭偰乮孞傝崬傫偱乯
堄枴偺偁傞桳尷抣傪弌偡偙偲傪暔棟妛偱偺尵梩偱乽孞傝崬傒乿偲尵偄傑偡偑丄
忋婰偺抣偑偦偺堦椺偲峫偊傜傟傑偡丅
僆僀儔乕偺婏柇側寁嶼偑弌偨偮偄偱偵丄僆僀儔乕偺嵟傕寖偟偄寁嶼
乮敪嶶偑僛乕僞乕偺応崌傛傝寖偟偄両乯傪徯夘偟傑偡丅
侾両亅俀両亄俁両亅係両亄俆両亅俇両亄俈両亅丒丒丒亖侽丏係侽俁俇俆俀俇丒丒丒
亙崱傑偱偺僆僀儔乕偺乽柍尷夝愅擖栧乮侾乯乿偺尨峞偼丄
乽悢妛偺柌丂慺悢偐傜偺傂傠偑傝丂乿崟愳怣廳丗娾攇彂揦丂傪嶲峫偵偟偰丄
懡偔偺堷梡偟偰偄傑偡丅亜
戞俀栭偺偲偒偵丄埲壓偺偙偲傪彂偒傑偟偨偹丅
僛乕僞乕娭悢兡乮倱乯偺慺惏傜偟偄偺偼倱偵偳傫側暋慺悢傪戙擖偟偰傕丄
堄枴傪帩偮偲偄偆揰偱偡丅亙悢妛揑偵偼乽夝愅愙懕壜擻乿偲尵偄傑偡亜
僆僀儔乕偺尒偮偗偨宍乮侾俈係俋擭乯偱尵偄傑偡偲丄
倱亝侽偺偲偒丄寧栭偺悽奅
侽亝倱亝侾偺偲偒丄偨偦偑傟偲偒亙梉從偗丒挬從偗亜
侾亝倱偺偲偒丄拫娫懢梲偺悽奅
偲儐僯乕僋側寧偺儅乕僋偲懢梲偺儅乕僋傪彂偄偰偄傑偡丅
寧栭偺悽奅偱偺晄巚媍側寁嶼偼偙偙偱丄廔傢傝偵偟傑偟偰丄
拫娫偺寁嶼偵堏傝傑偡丅
僆僀儔乕偼侾俈俁俆擭偵丄弴師兡乮俀倣乯乮倣亖侾丆俀丆丒丒丒侾俁乯傪寁嶼偟傑偟偨丅
兡乮俀俇乯偑嵟屻偱偟偨丅偪側傒偵丄
兡乮俀俇乯亖侾俁侾俆俉俇俀乛侾侾侽俋係係俉侾俋俈俇侽俁侽俆俈俉侾俀俆丒兾俀俇偱偡丅
幚偵嬃堎揑側寁嶼擻椡偱偡丅嬃扱偡傞偽偐傝偱偡丅
偙偙偱巹偙偲偱偡偑丄俁寧丆悢幃張棟乽俵倎倲倛倕倣倎倲倝們倎乿偺島廗夛 傪庴島偟偰偒傑偟偨丅 拫媥傒偵偙偭偦傝僜僼僩傪偍庁傝偟傑偟偰丄 変偺僆僀儔乕偵嬤偯偙偆偲巚偄傑偟偰丄僛乕僞乕兡乮倱乯偺抣偵挧愴偟傑偟偨丅
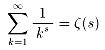
俵倎倲倛倕倣倎倲倝們倎偼執戝側僜僼僩偱偡丅弖帪偵寁嶼偟偰偔傟傑偡丅
巹偺庤尦偵丄兡乮俀倣乯乮倣亖侾丆俀丆丒丒丒俀俀乯丂偺抣偑偁傝傑偡丅
兡乮俁乯偺抣偼弌傑偣傫偱偟偨偑丄僆僀儔乕偵彮偟偱傕嬤偯偗偨傛偆側姶摦偑桸偄偰棃傑偟偨丅
榖傪杮戣偵栠傝傑偡丅
偁偺儀儖僰僀偑尋媶偟偨儀儖僰僀悢偵挧愴偟偰偄偒傑偡丅
偝偰丄栤戣偱偡丅
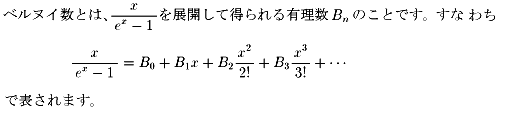
偙偺俛値偺抣傪俛侽偐傜俛俉傑偱丄媮傔偰偔偩偝偄丅
偙傟偱丄戞俆栭傪暵偠傑偡丅偍媥傒側偝偄丅

| NO.478 | '99 5/17 | 昹揷丂柧枻 | 俀n偺榓乮侾乯 |
拞俁偺惗搆偐傜偙傫側幙栤偑棃傑偟偨丏 斵偼寁嶼偑岲偒傜偟偔丆偨傑偨傑偙傫側嫽枴怺偄寁嶼寢壥偵婥晅偄偨偦偆偱偡丏 俀n乮値亞俁)傪師偺傛偆偵彂偒暲傋偰丆崌寁偡傞偲俋偑暲傇偲偄偆偺偱偡丏
| 俀3 | 俉 | |||||||||
| 俀4 | 侾 | 俇 | 丂 | |||||||
| 俀5 | 俁 | 俀 | ||||||||
| 俀6 | 俇 | 係 | ||||||||
| 俀7 | 侾 | 俀 | 俉 | |||||||
| 俀8 | 俀 | 俆 | 俇 | |||||||
| 俀9 | 俆 | 侾 | 俀 | |||||||
| 俀10 | 侾 | 侽 | 俀 | 係 | ||||||
| 俀11 | 俀 | 侽 | 係 | 俉 | ||||||
| 丒丒丒 | 丂 | |||||||||
| 崌寁 | 俋 | 俋 | 俋 | 俋 | 俋 | 丒 | 丒 | 丒 | 丂 |
幚嵺偵僾儘僌儔儉傪嶌偭偰憱傜偣偨偲偙傠丆
嵟崅俆侽侽侽寘偱俁係俋係寘傑偱俋偑暲傇偙偲傪妋擣偟傑偟偨丏
扤偐偙偺尨棟偵偮偄偰丆夝柧丆傑偨偼徹柧偟偰乮偁傞偄偼惗搆傪墝偵姫偔曽朄傪嫵偊偰乯
偄偨偩偗傑偣傫偱偟傚偆偐丏抪偢偐偟側偑傜丆巹偼偙偆偄偆偺偑嬯庤偱偡丏
僾儘僌儔儉傪慻傓偺偑惛堦攖偱偡丏
俻俛俙俽俬俠僾儘僌儔儉
'noguchi2.qb
CLS : max = 5000: DIM a(max), b(max)
a(0) = 0: a(1) = 8: b(1) = a(1): keta = 1: kaisuu = 1
FOR j = 2 TO max: a(j) = 0: b(j) = 0: NEXT
WHILE b(max) = 0 AND INKEY$ = "": kaisuu = kaisuu + 1
FOR j = 1 TO keta: a(j) = 2 * a(j): NEXT
FOR j = keta TO 1 STEP -1
IF a(j) > 9 THEN a(j - 1) = a(j - 1) + INT(a(j) * .1): a(j) = a(j) MOD 10
NEXT
IF a(0) = 1 THEN
keta = keta + 1
FOR j = keta TO 1 STEP -1: a(j) = a(j - 1): NEXT: a(0) = 0
END IF
FOR j = kaisuu - keta + 1 TO kaisuu: b(j) = b(j) + a(j - kaisuu + keta)
NEXT
FOR j = kaisuu TO 1 STEP -1
IF b(j) > 9 THEN b(j - 1) = b(j - 1) + INT(b(j) * .1): b(j) = b(j) MOD 10
NEXT
count = 0: owari = 0: j = 1
WHILE owari = 0 AND j <= kaisuu
IF b(j) = 9 THEN count = count + 1 ELSE owari = 1
j = j + 1
WEND
LOCATE 1, 1: PRINT 2; "^"; kaisuu + 2; "("; keta; "keta)"
PRINT 9; "->"; count: PRINT "others->"; kaisuu - count
WEND: WHILE INKEY$ <> "": WEND: END

| NO.479 | '99 5/18 | Junko | 俀n偺榓乮俀乯 |
椺偊偽丄俀10傑偱偵嬫愗偭偰峫偊偰傒傑偟偨丅
俽亖俀3丒侾侽7亄俀4丒侾侽6亄俀5丒侾侽5亄
俀6丒侾侽4亄俀7丒侾侽3亄俀8丒侾侽2亄
俀9丒侾侽10亄俀10
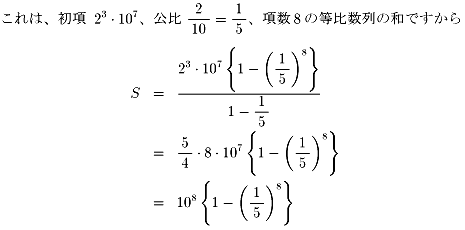
偙傟偼丄侾侽8傛傝彮偟彫偝偄悢(濨枂側昞尰偱偡偑丒丒丒)偲偄偆偙偲偱偡丅
幚嵺偵偼丄99,999,744偲側傝丄侾侽8亅俀8亖100,000,000-256偲
側偭偰偄傑偡丅
堦斒偵俀N傑偱寁嶼偡傞偲丄
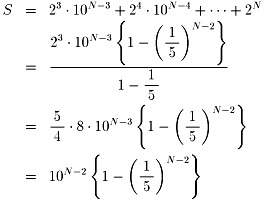
偙傟偼丄侾侽N-2亅俀N-2偲昞尰偟偰傕偄偄傢偗偱偡偑丄
忋偐傜偐側傝偺寘傑偱乽俋乿偑暲傇偩傠偆偙偲偑傢偐傝傑偡丅

| NO.480 | '99 5/18 | 寧偺岝 | 俀n偺榓乮俁乯 |
傑偢俽n傪師偺傛偆偵峫偊傑偡丅
俽3=8
俽4=80+16=96
俽5=800+160+32=992
乧
俽n=23亊10(n-3)+24亊10(n-4)+乧
+2n亊100
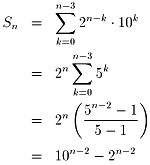
偲側傝傑偡丅
n偑戝偒偄偲偒10(n-2)偼 2(n-2)偵斾傋偰偲偰傕戝偒偄偺偱
俋偑偄偔偮傕懕偔偲偄偆傢偗偱偡丅
傑偨丄10(n-2)偼(n-1)寘丄2(n-2)偼 [(n-2)log2+1] 寘偩偐傜丄
俽n偼忋偐傜(n-2)-[(n-2)log2] 屄俋偑懕偒傑偡丅
俽n偼(n-2)寘側偺偱俽5002偼5000寘丄5000-5000 log2=3494.85乧側偺偱
忋偐傜3494屄偺俋偑暲傃傑偡丅
[ ]偼僈僂僗婰崋偱偡丅

| NO.481 | '99 5/19 | 寧偺岝 | 俀n偺榓乮係乯 |
俀偺戙傢傝偵俆偱傕忋偐傜俋偑暲傃傑偡丅
俀偺偲偒偲摨偠傛偆偵俿n傪 n亞侾偱師偺傛偆偵偟傑偡丅
俿1=5
俿2=50+25=75
俿3=500+250+125=875
乧
俿n=51亊10(n-1)+52亊10(n-2)
+53亊10(n-3)+乧
+5n亊100
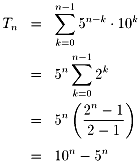
偙傟傕n偑戝偒偄偲偒10n偼 5n偵斾傋偰偲偰傕戝偒偔側傝傑偡偑丄
2n偺偲偒傎偳嵎偼戝偒偔側偄偺偱丄
忋偐傜楢懕偟偰暲傇俋偺屄悢偼彮側偔側傝傑偡丅
偦偺屄悢偼 n-[nlog5]側偺偱俿n偑5000寘偺偲偒
5000-[5000log5]=1505 屄偲側偭偰2偺偲偒偺 3494屄偺敿暘埲壓偵側傝傑偡丅
俽n偲俿n偺抣傪偄偔偮偐彂偄偰傒傑偡丅
| 俿1=5 | |
| 俿2=75 | |
| 俽3=8 | 俿3=875 |
| 俽4=96 | 俿4=9375 |
| 俽5=992 | 俿5=96875 |
| 俽6=9984 | 俿6=984375 |
| 俽7=99968 | 俿7=9921875 |
| 俽8=999936 | 俿8=99609375 |
| 俽9=9999872 | 俿9=998046875 |
| 俽10=99999744 | 俿10=9990234375 |
| 乧 | |
| 俿20=9.999990463E+19 |

| NO.482 | '99 5/20 | 昹揷丂柧枻 | 抲姺愊暘乮侾乯 |
俋俈擭偺戝嶃晎棫戝妛擖帋栤戣偱丆
乽嵗昗暯柺忋偵丆尨揰俷傪拞怱偲偡傞敿宎俀偺屌掕偝傟偨墌俠偲丆
偦傟偵奜懁偐傜愙偟側偑傜夞揮偡傞敿宎侾偺墌俠'偑偁傞丏
墌俠'偺拞怱偑(俁,侽)偵偁傞偲偒偺俠'懁偺愙揰偵報俹傪偮偗丆
墌俠'傪墌俠偵愙偟側偑傜妸傜偢偵夞揮偝偣傞丏
揰俹偺昤偔嬋慄偱埻傑傟偨椞堟偺柺愊傪媮傔傛丏乿
偲偄偆偺偑偁傝傑偟偨丏
夝摎偼丆
俹(倶丄倷)偲偟丆俷俙偺倶幉偲偺側偡妏傪兤偲偡傞偲丆
倶亖俁cos兤亅cos俁兤丆倷亖俁sin兤亅sin俁兤乮侽亝兤亙俀兾乯
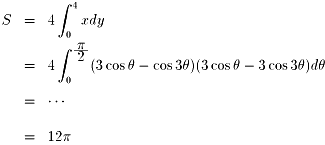
偲偄偆昗弨揑側抲姺愊暘偺寁嶼偱偡丏
偙偺栤戣傪師偺傛偆偵夝偄偨惗搆偑偄傞偺偱偡丏
偙偺夝摎偺偳偙偑堘偭偰偄傞偺偐丆偲偄偆偺偑幙栤側偺偱偡丏
| 儮俽 | 亖儮兤(倶2亄倷2)乛俀 |
| 亖儮兤{(俁cos兤亅cos俁兤)2亄(俁sin兤亅sin俁兤)2}乛俀 | |
| 亖儮兤(俆亅俁cos俀兤) |
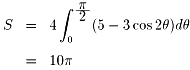

 E-mail
E-mail
 栠傞
栠傞