Weekend Mathematics/コロキウム室/1997/NO.5
NO.33 9/4 MK142857
今晩は。早いもので、夏休みもあっという間に終わってしまいましたね。
最近考えた問題を1つ送ります。
問題 8
どの頂点にも4つの正三角形と1つの正方形が集まっている
多面体について考えます。
この多面体の正三角形の面と正方形の面の数はそれぞれ
いくつずつになりますか。
ところで、このような問題では、
オイラーの多面体の定理をよく利用しますが、
この定理はまだ自分で証明したことがありません。
どうやって証明すればよいのか教えて下さい。
NO.34 9/15 Junko
オイラーの多面体の定理についてです。
一般に平面上や空間の中の図形Kが三角形分割されているとき、
三角形の数fと、辺の数eと、頂点の数vを数えて
χ(K)=v-e+f
とおいて、χ(K)をオイラ-数といいます。
三角形分割でない場合も何本かの辺を加えることで、
三角形分割にすることができます。
その際、加えた辺の数とそれによって増えた面の数が同じなので、
オイラ-数はかわりません。

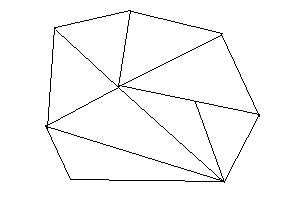
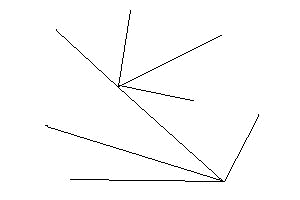
すると、閉じた道を含まない線系ができ、これを樹形と呼びます。
χ(樹形)=1となります。
つながった辺と頂点を1つずつ組にしていくと、
必ず最後に頂点が1つ残るからです。
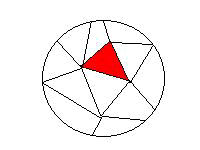
従って、χ(球面)=χ(K)+1 =1+1 =2
参考図書
NO.35 9/17 Junko
問題8についてです。
サッカ-ボ-ルのような立体を
イメ-ジしましたが、どうでしょう?
面の数をf、頂点の数をv、辺の数をeとすると、
オイラ-の多面体の定理より、
f+v=e+2・・・(1)
更に、三角形の数をt、四角形の数をsとすると、
t+s=f・・・(2)
三角形の辺の数は3、四角形の辺の数は4だから、
多面体全体で辺の数は、
3t+4s
ただし、これは2重に数えているので、
3t+4s=2e・・・(3)
1つの頂点に三角形は4つだから、
多面体全体で三角形の個数は、4v
ただし、これは3重に数えているので、
4v=3t・・・(4)
1つの頂点に四角形は1つだから、
多面体全体で三角形の個数は、v
ただし、これは4重に数えているので、
v=4s・・・(5)
以上5つの式を連立方程式として解きます。
(2)と(3)を(1)に代入します。
t+s+v=(3t+4s)/2+2
全体を2倍し、整理すると、
2v=t+2s+4
更に、(4)と(5)を代入します。
2v=4v/3+2v/4+4
これより、v=24
(4)と(5)に代入することにより、
t=32、s=6
つまり、三角形32個、四角形6個というわけです。
今度、ひまをみつけて模型を作ってみようかしら?
NO.36 9/20 みかん
問8の問題ですが、
四角形が6 三角形が32は分かりました。
そこで質問、この多面体は何種類できますか?
2種類できるように思うのですが・・・。
NO.37 9/22 Junko
よくわかりませんので、模型を作ってみました。

この多面体は球に近い形をしていて、
両極に当たる部分に正方形をおくと、
(この正方形同志は45度ずれています。)
赤道上に4つの正方形が斜めに位置します。
その隙間を埋めるように32個の正三角形が並びます。
そして、任意の2つの正方形同志の位置関係は
すべて同じで、
写真にあるように2種類あるようです。(違いがわかりますか?)
この結果を理論的に示すにはどうしたらいいのでしょう?
NO.38 9/23 よふかしのつらいおじさん(No.32を受けて)
No23についての感想。
"学校"という場所で、
中学・高校・大学と10年間も英語を学習したり
使っているのに、
なぜ日本人が英語をうまく話せないかについて。
急に中学で英語を教えるはめになった
元高校数学教師(にわかいんちき英語教師)の感想
まず、"学校"で英語を学んでいるということが
構造的にそれを可能にしにくくしていると思います。
教える目的が担当者ごとに色々だといいうことです。
英語を「聞ける・話せる・読める・書ける」ようにという
道具としての熟練を目指すこと、
自分たちの文化とは異なるまた別の知的体系を
総体として知ること、
英語という教材を媒介として担当者の持っているもの
(理念など)を伝達する・・・。
学校で教えるということは、
英会話教室や予備校で教えることと質や
目的が自ずと異なると思います。
そうであるので僕が"学校"の英語の教員として
採用される余地がありえると思います。
これが英語教室であれば教員としては
採用の余地はありえません。
"学校"というところは目的や意識の異なる
多様性を持った集団で構成されています
多様性に対応するためにはそれぞれ適当な
ところで妥協せざるをえず熟練の完成までは
目指せないということです。
もちろん時間的な余裕もありません。
中学1年は3単位です。
"Do you have a book ?" に対して "Yes, I do. "
と自然に言える生徒は半分もいません。
どこかで訓練した子(熟・英語教室・帰国子女など)
が可能です。
多くの子は少し考えてbe動詞でないから"Yes, I am."
でない方だ、という感じです。
担任をしていると授業を受ける態度とか
仲間と協調できるかというようなことも大事なことになります。
結果(授業の内容を身につけること)よりも
グループの中の役割をうまくやれているかの方が
大切になってきます。
英会話教室では会話の習得のみが目的になりえますが
"学校"の英語ではそうはできません。
次に、"教室"で学ぶということは
あくまで模擬的なもので、
必然性を伴った中での学習
ではないということです。
"Write apple." 、"Draw an apple."、
"Paint the apple."の違いを感じることは
なかなか大変だと思います。
下手に訳すと「りんごをかけ」で
日本語で考えると区別がなくなってしましいます。
"Write ABC."、"Write 123."、"Write あいうえお."
などを経験していると"apple"と綴れると思います。
"Draw a line."、"Draw a circle."、
"Draw a picture of Mt. Fuji."などを経験してい
るとりんごの絵を描けると思います。
最後のはりんごの絵に色を塗るのか実物に
ニスでも塗るのかその辺だと思います。
多分普通の人は伝えたい内容を日本語で考えています。
「かく」と言う内容を表すときに "write"、"draw"、
"paint" に対して自分の必然性を伴った経験がないので
すぐに適当な言葉を選ぶことができないのだと思います。
外国語として学ぶ場合に"Hey."と 言われても実感を伴わないと思います。 辞書に「注意を引いたり驚きを表したり質問を発したり するときの発声」とありますが、 文の前後を考えてこの場合は驚いているんだろうとかいう 具合に1クッション入るのではないかと思います。 場面に応じた英語の音の経験がないのでこれで いいのかどうか自信が持てないのだと思います。
さらに、日本人はほぼ単一民族であることだと思います。
島国であったため自分とは異なる民族に対したとき、
素直に受け入れられない部分があると思います。
例えばアメリカのように様々な民族が周りにいる
状況とは違うのではないかと思います。
日本人の心の中に人種に対する入り組んだ偏見は
潜在的に強くあるのではないかと思います。
(他の人種を卑しむだけでなく、
自分自身も卑しんだりして、
白人の持つ人種差別より込み入っていると思います)
だから、いざ白人を目の前にして何か
言わなければならないはめになったとき、
必要以上の圧迫を感じるのだと思います。
 戻る
戻る