NO.23 8/4 S.I.
あるサイトで読んだのですが、
最近またまた教育過程が変ったようですね。
最近でもないのかもしれませんが。
数学では複素平面が入ってきたようですが、本当でしょうか?
私の姉(S32年生まれ)の数学3の参考書を昔借りて
勉強していたら、複素平面(複素数平面というべきですか?)
が入っていて驚いたことを覚えています。
なぜなぜまた復活したのでしょうか?
数学の世界でそんな時代の要請があったのでしょうか?
数学に関係ないことで申し訳ないですが、
何とか審議会とやらが、
「大学入試の科目から英語をなくす」という、
トンデモ審議結果を出したそうですが、本当なのでしょうか?
私、アメリカに居り、英語では苦労しております。
日本人の英語下手は有名なのですが、
私の分析している理由は以下のものです。
- 日本語は子音+母音(あ行は母音だけ)で、
音を構成させているが、英語では子音だけの音があり、
これが重要。
ところがそれを聞き取る訓練ができていなかった。
- 文法的に、日本語は前から後ろへ修飾がかかっていくのに、
英語では後ろからどんどん修飾をかけていく。
語順の違い。
日本語は助詞(て、に、を、は、、、)で、
自由に語順を動かせる。
ところが英語では主語+動詞+目的語、、、
と語順が意味を固定する。
語順にフレキシブルに構えている日本人は
発想として慣れていない。
- 日本語は内容豊かであるが、英語はその点貧弱。
意味を取るとあまりに簡単すぎてスカみたいに感じる。
とにかく日本人の英語下手は日本語と英語の違いが
あまりに大きいのが主な理由でしょう。
ヨーロッパ語族なんか、文法がほとんど似ていますから、
単語の差し替えさえすれば簡単に英語になるわけです。
(独文英訳でもやれば明確です。
英語にすればかえってやさしい。)
何とか審議会のおっさんの考えるような、
入試のために実用英語とかけ離れた英語を
勉強させるからなんていうのが理由ではありません。
入試から英語が無くなれば、英語はもう単なる副教科です。
そうなったら、ただでさえ英語ができない日本人が
どうなることでしょう。
特に最近は文法軽視とか。
そりゃあ、幼児期にやるならいいでしょうが、
ある程度の年齢になったらそれは無理です。
昔、駿台にいた伊藤先生がやっておられた、
英語の仕組と文の成り立ちを一度分析意識化して、
その後、英語を理解する頭の働かせ方の訓練をする、
というのが今思うと一番正解でした。
学校文法の見直し
(I wished I could have been taught mathematics by you.
なんてそんな文を会話している人はいません。)
やヒアリング、会話の重視、それから、
言いにくいけど英語の先生の発音の改善、、、
などやることは他にあると思いますが、
入試から英語をなくせばいい、とは何とも短絡的な結論です。
英語の先生はなんて言っておられます。
(でもこのニュース自体が本当なのだろうか?)
NO.24 8/7 Junko
教育課程については、勉強不足で大したことは答えられないと思います。
94年度入学の生徒から、今の教育課程に移行しました。
根幹となる数学Ⅰ、Ⅱ、Ⅲと
オプション科目である数学A、B、Cとで構成されています。
高校の多様化に合わせて、各学校ごとにカリキュラムを編成
できるようにという配慮(?)でしょうか。
ご指摘の複素数は数学Bの中の1単元です。
数学Bはオプション科目ですから、
数学的(?)に絶対必要というわけではないと思います。
数学Aについて少し話します。
数学Aには、次の4つの単元があります。
- 数と式(展開や因数分解など)
- 数列(等差数列、等比数列、Σ、漸化式など)
- 平面幾何(メネラウスの定理、三角形の五心、変換など)
- 計算とコンピュ-タ-(コンピュ-タ-、ベ-シック、表計算など)
この中から学校ごとに選んでカリキュラムを組むわけですが、
ほとんどの学校が、1.数と式 と 2.数列 ではないでしょうか。
これって、個人的な好みなのではないかしら、と思うものや、
今時ベ-シックねえ、確かにアルゴリズムの勉強にはいいのかも、という感じですよね。
また、数年前までは、(私が高校生の時もそうでした。)高校に入学すると
まず、展開や因数分解といった計算の基礎となるものを学習しました。
ところが、これが数学嫌いを生み出しているというわけで、
オプション科目である数学Aにまわされてしまいました。
では、実際の場面で因数分解が必要になったらどうするのか。
必要になったところで学習しなさい、という現地調達方式と呼ばれるものです。
これでは、生徒は余計にわかりにくくなると思うのですが・・・。
現実には多くの学校が従来通り、つまり入学したての1年生に対しては、
数学Ⅰに入る前に数学Aの数と式の項目を学習するということを行っているのではないでしょうか。
確かに教育課程の編成というのは大変な仕事だとは思いますけれども、
もう少ししっかりやってほしいなと思いますね。
NO.25 8/7 MK142857(No.20を受けて)
小島淳子 先生 こんばんは。
さて、問題7についてですが、
予め当てはめられている数字がないときは、
答えがたくさん存在します。
ところが、問題のように1、3、5を固定すると、
うまい具合に答えが1つに定まるのです。
ところで、その答えの導き方ですが、
この図形の性質を調べれば、試行錯誤を減らすことができます。
問題のように、1、3、5を固定したのは
この図形の性質をうまく利用して解けるようにするためです。
僕は次のような解答例を用意しました。
図1で、一直線上の4つの数の和は26になりますが、
星印をつけた4つの数の和も26になるのです。
なぜなら、図1で、12個の数の和は、
1+2+3+・・・・・+12=78で、
また、星印をつけていない8つの数の和は
一直線上に並ぶ4つの数の和の2倍に等しく、
52となるので、
星印をつけた4つの数の和は26(=78-52)となるからです。
図1 図2
☆ 1
◯ ◯ ◯ ◯ ◯ c ◯ ◯
☆ ☆ a b
◯ ◯ ◯ ◯ 5 ◯ ◯ ◯
☆ 3
これより、図2のようにa,b,cを定めると、
1+a+b+3=26より、a+b=22
よって、(a,b)=(10,12),(12,10)となりますが、
a=10とすると、c=26-(1+10+5)=10 となり、
a=cとなって不適です。
これから(a,b)=(12,10)と決まり、
cは8(=26-1-12-5)となります。
ここまでの結果を全て当てはめると、図3のようになります。
図3 図4
1 1
◯ 8 ◯ ◯ d 8 e f
12 10 12 10
5 ◯ ◯ ◯ 5 g h i
3 3
次に、2がどこに入るか、考えるため、
図4のようにd,e,f,g,h,iを定めます。
2がg,h,iのいずれかに入ると仮定すると、
この3つのうちの残りの2つの和は、19(=26-2-5)となりますが、
8、10、12が使えないため、ここで行き詰まります。
これから、2はd,e,fのいずれかに入り、
d,e,fのうち2以外の2つの和が16になるため、
d,e,fは小さい順に2、7、9となります。
つまりeには2、7、9のいずれかが入りますが、
e=2とすると、i=13 、e=7とすると、i=8となり、
いずれの場合も不適なので、e=9と決まり、
同様にして、d=7となります。
以上の結果を全て当てはめたのが図5ですが、
ここまで数字がわかると、
残りは一直線上の4つの数の和が26であることを利用して
簡単に求めることができます。
こうして、最終的な結果は図6のようになり、
このとき、確かに一直線上の4つの数の和は等しくなっています。
図5 図6
1 1
7 8 9 2 7 8 9 2
12 10 12 10
5 g h I 5 4 11 6
3 3
僕は、この問題を考えたのは中学二年生のときです。
このように星形の図形に数字をうまく当てはめると、
一直線上の数の和をみな等しくできる、
という事実を知ってから、
なるべく少ない試行錯誤で解け、
また答えが1つしか存在いような問題を作ってみようと思い、
この問題を考えました。
NO.26 8/8 のんべえ熊(No.23を受けて)
英語の教師でありながら、
英語教育そのものにはたいして興味がない上に、
知識も少ないということをお断りした上で、
できるかぎり自分の思うことをかいてみたいと思います。
駿台の伊藤先生はぼくも浪人時代に教わったことがあります。
まず、何とか審議会というのは、中央教育審議会のことらしいですが、
中教審の一番新しい答申の主たるものは、
ご承知のように、中高一貫教育の公的導入と飛び級制の承認ですが、
英語を入試からはずすというのは聞いたことがありません。
細かい答申部分に含まれていたのかもしれませんが、寡聞にして知りません。
ただ、去年だったか、その前の年だったか、
多摩大学のアメリカ人学長のクラーク氏が
入試から英語をはずす方針を打ち出したことは知っています。
この点に関するぼくの考えは、
入試からはずせとは言わないまでも選択科目の一つにすべきだとは思います
(英文科や外国語学部はべつとして)。
現状では、4年制大学のほとんどの学部が、
文系、理系を問わず、英語を入試に課しています。
一般教養として、日本人のすべて(または、大学へ進むものすべて)
が英語ができなければならない、
という観念をまず払拭する必要があると思います。
この観念が日本人の英語コンプレックスの背景にあるとぼくは思っています。
確かに、文系理系を問わず、「英語ができたほうがいい」
ということはいえると思いますが、
すべての学問の必要条件というほどではありません。
逆説的に聞こえるかもしれませんが、選択にするほうが、
日本の英語教育の質、さらに、
日本人の英語能力の質を高めることにつながると思うわけです。
ついでに言うなら、高校での英語も選択にすべきです。
実際、高校英語は本来選択教科である外国語の一科目ですが、
実態として、英語をやらずに卒業できる高校はないのが現状です。
それを本来の選択科目にすべきだと思うのです。
要点はこうです。英語はやりたいもの、興味があるもの、
必要だと感じているものがやればいいということです。
ただ、その代わり、必修としての英語に代わって、
さまざまなバリエーションの英語の授業を用意する必要があります。
話せなくても読む力だけでもつけたいものにはそれにみあった授業を用意し、
読めなくても、日常会話くらいはできるようになりたいものには、
それに見合った授業を用意するということです。
もっとも、日本においては学校以外でこのような力を磨くことは
メディアの利用を含めて十分可能な状態がすでに存在していますから、
なおさら選択でいいし、
また、学校ですべてのバリエーションを用意する必要もないと思います。
現在の英語教育では、やりたいものも、やりたくないものも、
必要だと思っているものも、
必要ないとおもっているものも一斉に教えているわけで、
その結果、教材にしろ、教え方にしろ、どうしても平均的なものにならざるをえない。
結局、誰にとっても、
さしたる効果をもたらさない無駄な労力を使うことが多いというのが
一般的な情況といえるのではないでしょうか。
選択にすることがそこを変えて行くきっかけになるはずです。
押さえておくべきことは、すべての日本人に英語教育は必要ないということです。
さて、日本人の英語へたの原因をS.I.さんは分析していますが、
1)と2)は当たっているのではないでしょうか。
1)は音声面に関するものですが、敷衍して言うならば、
日本語は発音に関しては極めて不精ものの言語で、
口の内外の筋肉をたいして使わずに発音できるし
、母音にしても5つ(かつては8つあったそうですが)というのは本当に少ない。
したがって、英語に限らず、
使う筋肉の多いほかの外国語の発音がだめなのは致し方のないことです。
しかし、これも学習の初期に十分な音声訓練をすればできるようになるわけで、
運動や楽器を習うのに似ていると思います。
つまり、いくつになってもそれなりにはできるようになるということです。
最近、小学校からの英語教育の導入が特に音声面での問題から叫ばれ、
実際に導入の方向性が強まっていきていますが、
ぼくが思うには、音楽の一部として、英語の歌を入れ、
その辺を少し膨らませればそれで十分だとおもいます。
2)は文法面での指摘ですが、
語順の問題が日本人が英語を身につけるうえで一番ベーシックな障害
となっていることは教えていてよく分かります。
読む、書く、聞く、話す、すべてにおいて障害となっています。
中でも、この方の言うように、修飾の語順が、
基本的な主語、動詞、目的語(補語)の語順の内部に
障害となって立ちふさがっています。
修飾語が一語ならば英語も日本語も基本的には前からの修飾ですが、
英語では2語以上になると、すべて後ろに回るわけです。
関係代名詞なども文としての修飾関係の一種です。
英語は核になる語を先に出して、
後からそれを修飾する言葉を何重にも、
次々と加えて行く事ができるわけで、慣れてしまえば便利です。
英語は結論を重視し、日本語はプロセスを重視するといっては言い過ぎですが、
そんな感じがしないでもありません。
後ろからの修飾という観念を捨てたほうがいいと思うのですが、
なかなかできません。
しょっちゅう後ろから矢印をかいて、修飾関係を黒板で説明したりしますが、
これはまずいやり方だなと思いつつやってしまっています。
さて、3)についてですが、この種の言い方は知識人といわれる人たちからも
出てくるものですが、ちょっと考えれば、
そんな事は言えるはずもないということが明白な、暴論というしかありません。
日本人の外国語(外国人)コンプレックスのうらにはこの種の日本語(日本人)
優越感があります。
よく、日本語がうまい外国人、とくに話すだけでなく、
書くのがうまい人に対して、日本語のような難しい言葉をどうして
そんなにうまく操れるのですか、などというのもそういったコンプレックスの表われ
です。理論的に考えても、ある程度の長い歴史を持った言語の一方が、
他方よりも優れているとか豊かであるということは、
あるバイアスを設定しない限り言えるはずがありません。
これは文化の優劣に直結しているわけで、
どの民族にも文化的優越感は付き物ではあるものの日本人は特に強いと思います。
もちろん、ある局面を想定した上での比較は可能なわけで、
たとえば擬音語や擬態語に関しては日本語のほうが豊かで、
その自由度も高いといっていいと思います。
他方、韻律に関しては、西洋言語、のみならず中国語も可能であるのに対して、
日本語の詩作においてはほとんど不可能といっていい。
言語にはそれぞれの特性があると言えるのみです。
日本語のほうが豊かだと感じてしまうのはコンプレックスでなければ
その豊かさを享受できるほどには英語に習熟していないということに過ぎません。
最後に文法について思うところを書いてみます。
ぼくが教員になったころ、(自分の高校時代もそうだった)
英語の教科書は読本、文法、作文の3種類で、
文法は必ず全部終わるかどうかは別として、
独立した教科書で行われていました。
それが、指導要領の改訂によって、表面上からは消えてなくなりました。
その裏には、英語きらいにさせてしまうのは文法重視の授業のせいであるとという
根も葉もない説があります。
その結果、表面から消えてなくなった文法は英語Ⅰや英語Ⅱという
それまでの読本の教科書の最後の部分に、申し訳程度に、
ほとんど十分な説明もなく付録のようにつけられて、
あとは教師たちが工夫をして、
文法嫌い故に英語嫌いにさせることのないよう努力せよということになりました。
文法は悪者扱いされて日陰者にされてしまったのです。
かわいそうな文法君というわけです。
その後、再度の改訂で、各レッスンの中に文法事項をちりばめて
その都度扱うようにはなったのですが、
体系的になっているとはとても言い難い情況です。
ある程度の体系が見えなければ文法など無意味です。
これほど中途半端なやり方はありません。
今でも教科書によっては文法用語にやたら神経質になって、
なるべく文法用語を用いないで、説明しようとしているものもあります。
それがかえってわからなくさせていることも気づかずに。
それもこれも、文法用語が文法嫌いやわからなさの原因になっているといった、
とんでもない思い違いによるものです。
実態としては、改訂後もほとんどのいわゆる進学校、ならびに、
私立の大半では、準教科書に格下げされた、
かつての文法の教科書や参考書を使って文法の授業を行ってきました。
ただし、名目は英語Ⅰや英語Ⅱ、現在では必修になったオーラルAやBとしてです。
文部省も県教委もこの事実には頬かむりです。
もっとも、そういう学校の事情は文法が大事だから続けているという面ばかりではなく、
教師にとって文法はおいしい教科であるという面も否定できないと思います。
つまり、文法は一番やりやすい教科でありうることは確かですし、
断定的にまたある程度論理的に説明できることから、
教師としての自尊心を磨梠ォさせてくれるので、
教師のほうが手放したがらないのです。
特に学問的に英語をやってきた人にはなおさらそこにアイデンティティーが
かかっているという面もあります。だから、どっちもどっちといえなくもありません。
ぼくの考えはこうです。やるべきことは文法を日陰者にすることではなく、
学校文法の再編成をすべきだったのです。
それには、かなりの時間と人手が必要です。
しかし、それをやる意味はあると思います。
細かなビジョンを持ちあわせているわけではありませんが、
部分的ですら、英語という言語をもっと分かりやすくする整理の仕方、
もっとわかりやすいまとめ方はあり得ると思います。
大局的には特に日本語との対比をもっと多用することによって、
日本語自身の性格も分かってくるような骨格にすべきです。
大学教授がすすんでこんな事に手を出すとは思えませんから、
こういう事にこそ文部省がプロジェクトチームを作るなり、
研究センターを作るなりすれば、まだ、存在意義はあるものの、
今みたいに余計なお節介しかできないような役所などないほうが、
よっぽど日本の教育事情は良くなるのは明らかです。
まあ、無理な希望的観測でしょうし、出版社にもそんな度胸はありません。
結局高校や中学の現場の教師ががんばるしかないのかなとも思います。
しかし、そんな暇をかこっている教師はまた、
ある面では問題でもあるわけです。
以上、思い付くままに書きました。
NO.27 8/11 shiba-shiba
実は聞きたい問題があり、数学関連のサイトを探しました。
それはルートの求め方です。
たとえばルート4は2であったりする訳ですが、
5乗すると1.306になる数というのはどうやって求めるのでしょうか。
これもあてずっぽで1以上2未満だとか。
1.05よりも大きいけど1.06じゃ大きすぎるとか
続けていって、
1.055当たりに落ち着いたのだけど、
ほんとうはどうやって計算するのですか 。
NO.28 8/20 Junko
ある数aの5乗根(5するとaになるもの乗)を
求めるということは、
方程式 x5=a、
つまりx5-a=0 を解くことに他なりません。
2次方程式ax2+bx+c=0の解が、
x=(-b±SQR(b2-4ac))/2aで与えられることは
中学校で勉強しますね。
手続きはかなり面倒ですが、一般の3次方程式、4次方程式にも
解の公式はあります。
ところが5次以上の方程式には、因数分解できるようなものはともかく一般的な解法はありません。
そこで、どうするかというと大体の見当をつけて近似していくという方法がとられます。
高次方程式f(x)=0の解の見つけ方
高次方程式の実数解は、y=f(x)のグラフとx軸との交点を求めればよいわけです。
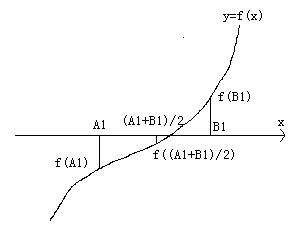
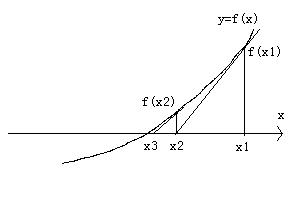
 戻る
戻る