Weekend Mathematics／コロキウム室／1998.7〜12／NO.23

 

NO.178 　　　 10/27 　　Junko 　　　　数理パズル（３）

問題２の数列ですが、ヒントに従ってそれぞれ英語に直してみたら あることに気がつきました。 さて、６６の次は何だろうかと考えていたら、 あれよあれよという間に どんどん進んで「２０００」、そして「２００２」となりました。 本当かなあ・・・？

英語に直した時に、そのspellの中に「e」のないもの。
奇数、１(one)、３(three)、５(five)、７(seven)、９(nine)はすべてだめです。 それと８(eight)もだめです。
さて、６８の次ですが、７０代(seventy-*)、８０代(eighty-*)、９０代(ninety-*)もだめ。 １００(hundred)もだめなので、３桁はすべてだめ。
４桁に突入し、１０００代(one thousand)がだめなので、 ２０００(two thousand)とそして次は２００２(two thousand two)というわけです。

spellの中に「e」が出てくるものが予想外に多いのにびっくりしました。

NO.179 　　　 10/27 　　水の流れ 　　　 平均物価上昇率

今から、４０年前はパン１個が１０円でした。 今では１個１００円です（消費税別）。
４０年の間に１０倍になりました。 それでは、１年平均の物価上昇率は一体いくらでしょう。
ヒント：これが相乗平均の例です。

NO.180 　　　 10/27 　　水の流れ 　　　 最短シュタイナー問題（１）

1. 三角形の頂点Ａ，Ｂ，Ｃの位置に３校があり、 この３校を連結するネットワーク （どの２校もネットワークを通して、行き来できるようにする） を結ぶ計画があります。 もっとも短い結び方で、何ｋｍの線が必要でしょうか？ また、その作図も書いてください。 ただし、ＢＣ＝ａｋｍ，ＣＡ＝ｂｋｍ，ＡＢ＝ｃｋｍ　です。
   
   
2. 正方形の頂点Ａ，Ｂ，Ｃ，Ｄの位置に４校があり、 この４校を連結するネットワーク （どの２校もネットワークを通して、行き来できるようにする） を結ぶ計画があります。 もっとも短い結び方で、何ｋｍの線が必要でしょうか？ また、その作図も書いてください。 ただし、１辺の距離はａｋｍとします。

NO.181 　　　 10/29 　　水の流れ 　　　 ジュ−スの問題（１）

問題の投稿
本日の文化祭で、私のクラスは「吉本新喜劇」を上演しました。 その慰労を兼ねて、 生徒全員にジュースを１本ずつプレゼントしょうと思います。 ５本のセットと９本のセットで売っている 缶ジュースを組み合わせてちょうど人数分だけのジュースを コンビニに買いにいきました。 しかし、どうしても人数分になるような買い方はできませんでした。 考えられる私のクラスの生徒は最大何人でしょうか。

NO.182 　　　 10/30 　　Junko 　　　 ジュ−スの問題（２）

ａ＝５ｍ＋９ｎ（ただし、ｍ≧０，ｎ≧０なる整数）という形に 書き表すことができない最大の整数ａを求めよということですね？
逆に言うと、ある数以上の数は必ず上述の形に書き表せすことができるというわけですね。

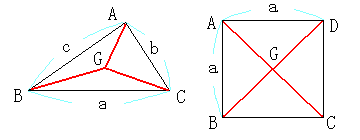
NO.183 　　　 10/30 　　Junko 　　　 最短シュタイナー問題（２）

三角形、ないし四角形の重心と各頂点を結ぶ線分の和になるのでしょうか？ 物理的に考えれば、角頂点において同じ力で引っ張ったときに、 釣り合う点かな？　だとしたら、重心ですよね？

E-mail 戻る