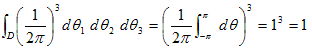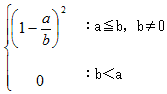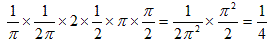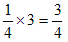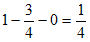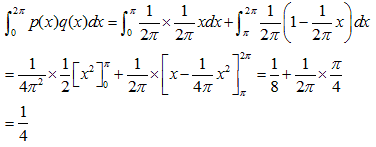ColloquiumNO.252
|
皆さん、場合の数が無数にある確率の問題を考えたことがありますか。ここで、問題です。
床一面に等間隔な平行線群がひかれています。いま、1本の針を任意に床上に落とすとき、
針が平行線の１つと交わる確率を求めよ。
ただし、平行線の間隔を４、針の長さを２とする。
注：ビフォンの針という問題です。
ヒント：針の中点から一番近い平行線と交わる条件を考えてみる。
注：この記事に関する投稿の掲載は、2010年2月15日以降とします。
No.1823ではやんちゃをやってしまったので、今度はちゃんと考えよう！。
「夜ふかしのつらいおじさん」と「kohji」さんの良いとこ取りをしよう、と思いました。ところが・・・。
まず、円周上の3点を角度θ1，θ2，θ3、
−π≦θ1，θ2，θ3＜πで表す事にして、それぞれの一点にまぐれ当たりする確率は、規格化定数を1/2πとして、1/2π×dθ1，1/2π×dθ2，1/2π×dθ3。
実際これらを領域Ｄ＝[−π，π]×[−π，π]×[−π，π]で積分すれば（[−π，π]は区間）、
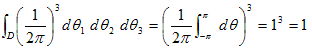
になる（夜ふかしのつらいおじさん方式）。
次に「kohji」さんのように、(θ1，θ2，θ3)に対する、
(1)直角三角形になる条件，(2)鋭角三角形になる条件，(3)鈍角三角形になる条件を書いてやって、その領域Ｒを定め、Ｒの各点に、重み1/2π×dθ1，1/2π×dθ2，1/2π×dθ3をかけて3重積分すれば、それがそのまま確率になる。これは体積比だが、面積比の親類という事で、水の流れ先生にも許してもらえるだろう。俺って何てハイセンス（←と自己満足）。
(1)直角三角形の場合
円周上の三点を、
(cosθ1，sinθ1)，(cosθ2，sinθ2)，(cosθ3，sinθ3)
とする。三角形は、どれか一つの頂点しか直角になれないから、それをθ1の点としよう。そして後で結果を3倍すれば良い。直角三角形の条件は余弦定理を使って、・・・エエト・・・余弦定理とユークリッド内積はいっしょだから・・・、
(cosθ1−cosθ2) (cosθ1−cosθ3)
+(sinθ1−sinθ2) (sinθ1−sinθ3) = 0
となる。・・・なんだ、三平方の定理といっしょじゃないか（←ちょっとがっかり）。
式は複雑そうだが、こちとら数値計算で食ってんだ！。こんなのExcelでもあれば、いくらでも計算できるぜ！（←と自己満足。でもこの考えがそもそも駄目）。
・・・待てよ、条件は単純化できる。今回は三角形の形さえ比較すれば良いんだから、3点のうち2点は水平に取ったって良いはずだ。とすれば、図-1を考えればよい。
図-1より、cosθ3＝−cosθ1，sinθ3＝sinθ1だから、
2cosθ1(cosθ1−cosθ2) = 0
ただし左右対称性から、−π/2≦θ1≦π/2，−π≦θ2＜πとなって、θ1方向の規格化定数はπ，θ2方向の規格化定数は2πで、領域Ｄは[−π/2，π/2]×[−π，π]だ。ほぉ〜ら、2次元の面積比になった！。そしてこんなの、Excelを持ち出すまでもないぜ！。
θ1＝±π/２
か、
θ1＝±θ2
に決まっとる！。
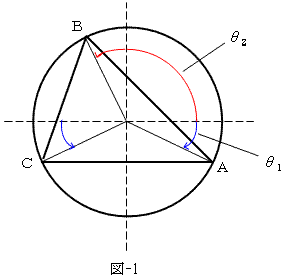
(2)ところが・・・
(1)の条件を、領域Ｄに重ねると、図-2の太線になる。
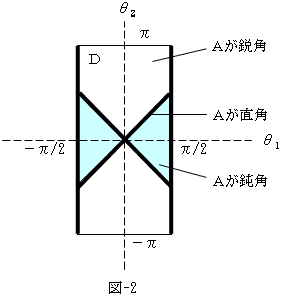
そうすると、領域Ｄに対する太線の面積比は、・・・面積比は・・・( ・ ＿ ・ )ｼﾞｰ・・・、0？。
エッ、エ〜〜っ！。なんですと〜〜っ！！(￣Д￣;) ガーン。
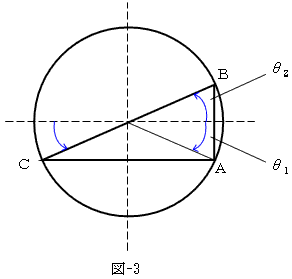
これは条件を間違ったか？。条件をちゃんと図にしてみよう。θ1＝±π/2は、三角形が潰れる場合だから、θ1＝θ2を図にすると、・・・（図-3作成中）・・・
・・・2点が直径に載る時だ。なんだ円周角の定理じゃないか（←要領の悪さに、再びがっかり）。だから条件は正しいと思える。しかし納得できない。図-3にように、3点を選ぶ事は現実に出来るじゃないか？。なのに確率0とはどうしてだ？。確率0とは、実現不可能という事じゃないのか？。
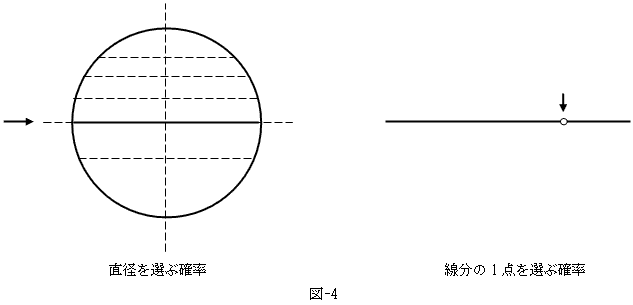
だけどこれは、円周上に2点とって、それが直径になる確率を求めるのといっしょだ（図-4の左）。2点を水平に取って良いなら（良いと思える）、これは半円周から1点にまぐれ当りする確率と同じだ。という事は、線分上の1点にまぐれ当りする確率と同じ事になる（図-4の右）。No.1817に戻って考え直そう。
(3)考え直してみました
No.1817で、長さbの線分上に、長さa以上になるように2点を選ぶ確率は（0≦a，b）、
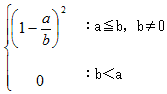
だった。aがbを越える時は、長さbの線分上に長さa以上の2点は選べないから、確率は0になる。当然だ。
しかしa＝bの時は？。この時も確率は0になるが、長さbの端点を現実に選ぶ事ができる。
・分布確率の場合の確率0とは、実現不可能な場合と、限りなく0に近いという、二通りの意味がある。
これが結論になりました。
なんとか面積比にする算段はしましたんで、やっぱり正解を教えて下さい・・・。
以下、一部修正(2/20)
(4) 鈍角三角形になる確率
以上が正しいとして、鈍角三角形になる確率は、鈍角になれるのは1頂点だけなので、
それをＡとすると図-2より、Ａが鈍角になる確率は、
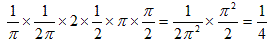
ＢだけもＣだけも鈍角になれて、それらは独立試行なので、
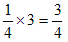
が、鈍角三角形になる確率。
(5) 鋭角三角形になる確率
三角形は、鈍角三角形でも直角三角形でもなければ、鋭角三角形なので、その確率は、
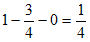
ところで、(2)にいたって、やっと問題のヒントの意味がわかりました。
最初から円周角の定理を使えば良かったのですね・・・。
(0)
考えやすいように円の半径を１とします。
円周の長さは２πです。
円周上に点をとるとき、どこを選ぶかに区別はありません。
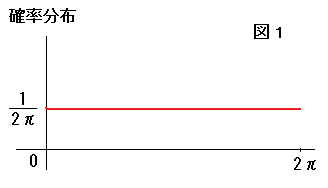
確率分布ｐ（ｘ）は定数と考えられます。
円周にそってｐ（ｘ）を積分すると１とならなければならないので、ｐ（ｘ）＝１／２π となります。
(1)
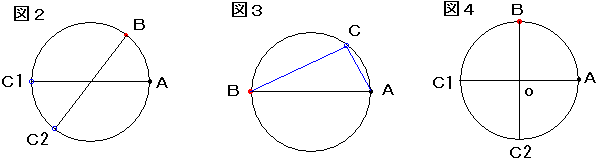
最初の点Ａはどこにとっても良いので右端にします。
２番目の点Ｂは適当に図２のようにとったとします。
△ＡＢＣが直角三角形になるにはＣと（ＡかＢ）とを結んだときに直径にならなければなりません。
（直径にたつ円周角は直角）
図２でＣ1にしてもＣ2にしても点なので円周の２πに対して長さの比の値は０と考えるのが適当です。
２番目の点ＢをＡＢが直径となるようとったとすると（図３）、点Ｃはどこにとっても直角三角形になります。
しかし、点ＢはＡに対しては１点しかないので、円周の２πに対して長さの比の値は０と考えるのが適当です。
以上から直角三角形になる確率は０です。
(2)
図２のように点Ａ、Ｂをとったとします。
△ＡＢＣが鋭角三角形になるには、点ＣはＣ1とＣ2の間にあれば良いことになります。
∠AOBがπになるまでは鋭角三角形になる確率は角の大きさに比例します。
∠ABO=π／2 のとき、鋭角三角形になる確率は、１／４です。（図４）
以上から確率ｑ（ｘ）は図５のように考えられます。
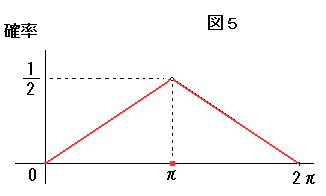
よって鋭角三角形になる確率は、
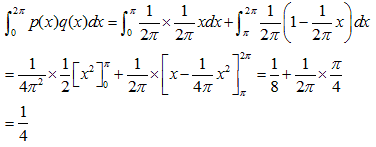
(3)
（１）、（２）より鈍角三角形になる確率は、
１−１／４＝３／４です。
