NO.1797 大学数学事始め(?) 2009.7.20. DDT
白状しますと自分は、大学で正式な数学教育も物理教育も受けていません
(教養の何とかは受けましたが)。独学と言えば聞こえはいいですが、ほぼ勝手気ままな無免許状態の自己流です。
最初のうちは、四輪車や単車どころか、三輪車のサドルにも座れないような状態でした。
ようやっと人並みに腰を落ち着けられるかな?、と思い出したのは、いくつかのひどく基本的な概念を了解した後です
(理解ではなく了解です)。いわゆる「大学数学の壁」を越えたのかな?、と思える瞬間がありました。
以下では、大学の数学を本気で眺めた時、最初にぎょっとする(事によったら、絶望的気分になるかも知れない)、
いくつかの概念についてコメントします。
これを書き出したのは5月も中旬の頃で、新高校3年生になった皆さんや、今春めでたく大学に入学された方々も
いるはずなので、時節柄ちょうど良いかなぁ、と思ったのですが、もう6月になります。
全く、大きなお世話になりそうです・・・。
1.集合
集合とは物の集まりの事です。ここで物は、何でもOKです。それ以上でもそれ以下でもありません。
「〜の全体」と言った瞬間に(〜が集まったと思った瞬間に)、集合はもう定義されています。
なので、集合を集めた「集合の集合」なんかも、数学では平気で出てきますが、「集合」という言葉が出てきたら、
「何か集めたな」と思えば良いだけです。ただし集め方(集合を定義する条件)が、非常に間接的だったり、
複雑になったりする事はあります(大学は専門職を養成する場でもありますから)。
以上は、素朴集合論の考えです。無限集合だとか、無限のパラドックスを回避する公理的集合論だとかは、
大抵の場合意識する必要もありません。何を言いたいかというと、「集合とは物の集まりで、物は何でもOK」
という程度の普通の感覚でOKなのだから、集合という言葉に過敏になる必要はない、という事です。
例:自然数全体の集合N({1,2,・・・}と集まったと思った!)
じつはNの中には無限個の要素がありますが、集まったと思った瞬間に、Nは存在すると考えています(普通は)。
2.構造
物を集めただけの集合で出来る事は、要素の個数をカウントするくらいで、集合内部に、
何か特長的な内部構造が生じる事はありません。自然数全体の集合N={1,2,3,4,5,・・・}には、
要素の順序が自然にあるように思えますが、N={5,10,1,1000,100,・・・}(← 順序なし)でもあります。
実際にはNを集めた後で、集合Nに順序構造を入れて、{1,2,3,4,5,・・・}と整列させている事になります。
集合の内部構造はふつう、部分集合の集合を考える事で発生します。部分集合の集め方を与えて、構造を定義するわけです。
この集め方は大抵ひどく間接的で、わかり難いものの典型になります。
例:位相構造の定義
集合Xの部分集合の集合Dが、次の条件を満たすように与えられてできる構造を、X上の位相構造と言う。
(O1) Dの集合の任意の合併は、Dの集合。
(O2) Dの集合の有限個の共通分は、Dの集合。
Dの集合は、この位相構造の開集合と言う。
こんなので「構造」が生じるの?、という気もしますが、実際にはこれだけで、かなりの事が言えるようになります。
それはTextを丹念に追えば、必ず了解できます。
3.写像
言ってしまえば写像とは、関数の事です。関数y=x2とか良く言いますし、放物線のグラフを想像します。
しかし、関数4=22とは言いません。どうしてかと言うと、4=22が放物線のグラフと結びつかないからです。
この場合暗黙の内にやっている事は、x全体の見渡しです。それでxは(独立)変数と言われます。
この独立変数の見渡しを、もう少し厳密に定式化したものが、写像の概念です。つまり、
| x | y
|
|---|
| 0 | 0
|
| 1 | 1
|
| 2 | 4
|
| 3 | 9
|
| ・
|
| ・
|
| ・
|
| x | x2
|
| ・
|
| ・
|
| ・
|
という「表」が任意のxを網羅して与えられたら、それで関数y=x
2は定義されたと考えます。
この方法の利点は、式にも書けない関数だって定義できるところです(表があればいいんだから)。
ところでxは、実数全体の集合R(実数が全部集まったと考えた)の要素の一つです。yもRの要素の一つです。
Rの各xに特定のyが対応して関数になっています。これを、f:R→Rと書いて、表を書く事を省略します。
またxやyがRに属する事を、x∈R,y∈Rと書きます。
対応を具体的に知りたい時は、f:x

x
2などと書きますが、
事によったら、f:x

[f(x)を定義する複雑な条件文]、
といった場合は無きにしも非ずです。よって関数はf(x)ではなく、関数fと書く事になります。
f(x)は、関数fのxにおける関数値f(x)=x
2です。しかし関数y=f(x)や、もっとひどく、
y=y(x)という言い方も良くします(便利なので)。これは、f:x

f(x)という意味です。写像の定義を挙げます。
定義1.(写像)
XとYを集合とする。各x∈Xに対して、xによって定まるy∈Yが一つだけの時、
この対応を写像と言い、f:X→Yと表わす。x∈X,y∈Yとわかっている時は、f:x  yとも書く。
Xを定義域,Yを値域と言う。
yとも書く。
Xを定義域,Yを値域と言う。
この一般的定義を読んだとき、自分に起きた最初の反応は、「全てのxについて、yは一つだけなのか?
」というものでした。数学の専門家からは、「そんなこたぁ〜、どこにも書いてない!」という一喝を受けるだけですが、
最初はみんな素人です。こんな疑問もなきにしも非ずだと思います。
数学は、最低限に言葉を切り詰めて記述します。なので、定義1.のどこにも「全てのxについて、yは一つだけ」などとは
書いていないので、異なるxには異なったyが対応しても良い事になります。もう一言いえば、異なるxに、
同じyが対応しても良い事にもなります。こんな例は、ごまんとあります。そんな時は、
最低限に言葉を切り詰めている事を、思い出します。慣れれば、文脈から判断できます。
次に、この一般的定義は一見虚しく感じられますが、じつは重要な含みを持っています。
一つは、任意のx∈Xに対して、必ず対応するyが存在しなければ写像でないという事です。
この制限は厳しすぎるように思えますが、定義を厳密化するためには必要です。
ただし実際には適宜判断し、対応するyが存在しないxは無視したりするのは自由です
(つまり、自由に定義域を狭めたりする事は可能)。
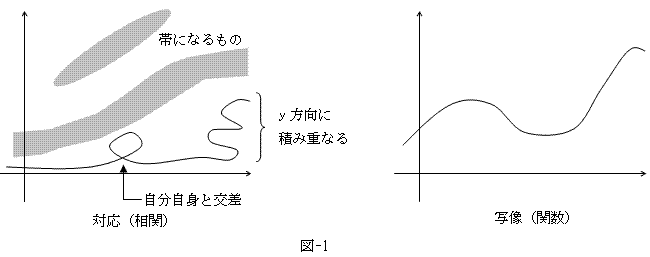
もう一つは、帯になるグラフは写像(関数)でない、という重要な結果です。
逆に言えば、関数(写像)のグラフは必ず曲線になります。そうでないものは、たんに対応とか相関と言われます。
ただし自分自身と交差したり、y軸方向に積み重なるような曲線も、定義1.から関数ではありません。
この場合は、まさに定義域や値域を適当に拡縮して、関数になるように「部分写像」を定めます。
「部分写像」の例は、少し後に述べます。
4.単射,全射,双射
写像の一般的性質として、特に役立つ性質が3つあります。
一対一の写像、上への写像、およびその両方の性質を持つ写像です。
標準的定義を述べれば、以下のようになります。
定義2-1.(一対一の写像)
f:X→Y,y1=f(x1),y2=f(x2)とする。
x1≠x2 ⇒ y1≠y2 である時、fを1対1の写像と言う。
(「⇒」は、「ならば」と読みます)
定義2-2.(上への写像)
f:X→Yとする。任意のy∈Yについて、y=f(x)となるx∈Xが存在する時、fを上への写像と言う。
定義2-1.の条件を満たせば、実際に写像fは、一対一の対応になります。何故なら対偶を取ると、
「y1=y2 ⇒ x1=x2」になるからです。
逆に言うと、「y1≠y2 ⇒ x1≠x2」や「x1≠x2
であってもy=y2となる場合もある」
は、写像では一般的に当然という事です。それは図-1の右側を見れば明らかと思いますが、
一対一でない典型例は、f(x)=x2です(y=x2)。
y=x2では例えば、+2≠−2に対してf(±2)=4ですし、y1=16,
y2=4のy1≠y2に対しては、
x1=±4,x2=±2で、必ずx1≠x2です。
これに対してf(x)=x(y=x)は、一対一です。「x1≠x2であっても
y1=y2となる場合」はなく、「y1≠y2 ⇒
x1≠x2」は当然満たし、この場合y=xである事から、
「y1=y2 ⇒ x1=x2」も当然となって、
対偶をとれば「x1≠x2 ⇒ y1≠y2」が成り立ちます。
一方、上への写像でない典型例もy=x2になります。何故なら、y=x2≧0なので、
y<0については、y=f(x)となるx∈Xは存在しないからです。これに対してy=xは、
上への写像の典型例です。それはグラフを想像すれば、すぐわかると思います。
以上の話は、y=x2とy=xのグラフを書けば、すぐに了解できる事です。
にも関わらず、言葉でもってそれらを説明しようとすると、上記のように面倒になります。
でもそれは数学において、やらざる得ない事態でもあります。何故なら「絵にも書けないグラフ」
を扱わざる得ない場合もあるからです。だとすれば使用可能な言葉として、できるだけ図形的直感を
反映したような用語を定めておくと便利です。ただし以下では、集合Aが集合Bの部分集合である事を、
A⊂Bと表わします。
定義3-1.(逆像)
f:X→Yとする。A⊂Yについて、f(x)∈Aとなるx∈Xの全体の事をAの逆像といい、
f-1(A)で表わす。f-1(A)は、Xの部分集合である(f-1(A)⊂X)。
特にYの一点{y}⊂Yの逆像を考える時は、f-1({y})と書かずに、f-1(y)と略記する。
全ての写像が上への写像ではないので、任意のy∈YやA⊂Yについて、
f-1(y)やf-1(A)が存在するわけではないが、その場合は、
f-1(y)=φ,f-1(A)=φと考える。
逆像に空集合φも認めれば、逆像を表わす定義域Xの部分集合は、常に存在する。
何故なら、任意の集合Xに対して、φ⊂Xだから。
定義3-2.(像)
f:X→Yとする。A⊂Xについて、f-1(y)⊂Aとなるy∈Yの全体の事をAの像といい、f(A)で表わす。
f(A)は、Yの部分集合である(f(A)⊂Y)。
特にXの一点{x}⊂Xの像を考える時は、f({x})と書かずに、f(x)と略記する。
写像の定義より、任意のx∈Xに対して、対応するy∈Yは必ず存在するので、
任意のx∈XやA⊂Xについて、f(x)やf(A)は必ず存在する。言い換えれば、
像を表わす値域Yの部分集合は、常に存在する。
逆像とは、指定されたy∈Yに写像して来るような、x∈Xを全て集めたものです。
写像y=x2の、Yにおける一点y=4の逆像は、f
(4)={+2,−2}⊂Xになります。
そして、y=−1の逆像は、f-1(−1)=φ⊂Xとなります。
逆に像とは、指定されたx∈Xが写像する、y∈Yを全て集めたものです。
Xの部分集合A={+2,−2}⊂Xの像とは、f(A)={4}⊂Yです。
逆像と像の用語を用いると、「一対一の写像」「上への写像」の定義は、かなり直感的になります。
定義4-1.(単射)
f:X→Yとする。任意のy∈Yについて、f-1(y)={x}である時、
すなわち一点の逆像が一点集合である時、これを単射と言う(「y1=y2 ⇒ x1=x2」と同じ条件。一対一の写像と同じ)。
ただしyがf(X)の外にある時は、f-1(y)=φであるが、φは0個の要素を含むとみなして、これも一点集合と考える
(一点集合より、さらに強力な一点。0個だから)。
定義4-2.(全射)
f:X→Yとする。f(X)=Yである時、これを全射と言う
(任意のy∈Yについて、y=f(x)となるx∈Xは、当然存在する。上への写像と同じ)。
定義4-3.(双射)
f:X→Yとする。fが単射かつ全射である時、これを双射と言う。
ただし双射という用語は、けっこうローカルなものである事を最近知りました。
ふつうはそのまま、全単射と言うみたいです。さらに図-1みたいな「概念図」は是非描くべきです。
何故なら、このような単純な「図」が、面倒な概念の理解を非常に助けてくれます。
現在の数学は、その基礎に集合論を置きました。集合論では、ある性質を言葉によって説明する事と、
その性質を満たす物供を全て並べて見せる事(集合を作ってみせる事)は同じだ、と考えます。
その立場では、言葉によって説明する必要はありません。「〜の集合を考える」という一言でもって、
全ては了解できるはずだ、という基本的態度が、現在の数学にはあります。これはある意味、
こと誤解を生じさせない点においては、ものすごく爽快な物ではありますが、初学者にとって、こんなに難しい物もありません。
何故なら、集合の全体イメージを想像できなければ、物事は了解不可能であり、その想像はふつう、
訓練によって達成されるからです。現在の数学は、初学者に過度の初期訓練を要求します。しかし対策はあります。
集合論が基礎という事は、逆に言うと原理的にはいつでも、「了解を補う概念図(イメージ図)」を描けるはずなのです。
何故なら集合によって、常に了解すべき対象を、即物的に全て並べて見せる事を行うからです。何らかの形で、
概念は常に可視化できます。
例えば、n次元のグラフの単射や全射を語るにしても、本質部分は図-1のような
「概念図」で十分だと、自分には思えます。集合は全てを並べて見せてくれる、
非常に即物的な理論なのだから、どんなに難解で複雑な話でも、概念図は書けたはずではないのかと・・・。
しかし現在の標準的Textの多くは、そうではありません。これは手抜きではないのか?。
いま自分は、そうではない事を知っています。現在の標準的Textの原典は、かなり古いものが多いです。
事によったら、前世紀初等とかいうのもざらです。その頃、例えば図-1にようなものを作るのが、
いかに難しかったのかを、いまの自分は知っています。
図-1のような他愛もない図さえ昔は、専門の印刷技術者にスケッチを渡し、何度も仕上がりを
イメージした「活版印刷」の結果を想像する、チェックと打ち合わせを行って、やっと「印刷物」になっていたのです。
その状況は、ほぼ1980年代まで続きました。
我々は今、技術革新による、ものすごい幸運の中にいます。図-1なんか自分は、たったの5分で作りました。
しかもたったの5分で作ったものが、そのままWebなどに載ったりします。30年前には、考える事すら出来なかった事態です。
だから言います。概念図を描きましょう。それについては、例えば現在のPC環境が、フルサポートしてくれます。
5.逆写像
逆写像は逆関数と同じです。逆写像は、単射,全射の概念の便利さを示す最も簡単な例になります。
また、定義域の任意の要素に必ず対応先がなければならないという、写像の定義における制限の妥当性を示す例にもなります。
f:X→Yが逆写像を持つ条件は、それが双射である事です。証明は簡単です。
写像f:X→Yの一般的な様子は、図-2にように書けます。
図-2において  は、f:X→Yを表わし、
は、f:X→Yを表わし、 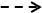 は、f:x
は、f:x  yを表わしています。図-2においては、f
yを表わしています。図-2においては、f
(y2)を表わす△と、f-1(y3)を表わす△とが重なっていますが(y2≠y3)、
fが写像なら、このような事はありません。何故なら二つの△が重なっていると、
その共通部分に含まれるx'∈Xから、等しくないy2とy3に2本の  が立ち、
f:x'
が立ち、
f:x'  y2,y3となって、
写像の定義に反するからです。
y2,y3となって、
写像の定義に反するからです。
さらに写像の定義から、△は  で表わした集合Xを隙間なく埋め、f(X)={y1,y2,y3,・・・,y,・・・}⊂Yは、
fが全射とは限らない事から一般には、f(X)≠Yである事もわかります。以上の事を念頭に置き、
逆写像(逆関数)f-1:Y→Xがあったとして、それが写像になる条件をさがします。
で表わした集合Xを隙間なく埋め、f(X)={y1,y2,y3,・・・,y,・・・}⊂Yは、
fが全射とは限らない事から一般には、f(X)≠Yである事もわかります。以上の事を念頭に置き、
逆写像(逆関数)f-1:Y→Xがあったとして、それが写像になる条件をさがします。
逆写像(逆関数)f-1:Y→Xとは、y=f(x)なら、
f:y  xとなるようなものなので、
図-3以外にはあり得ません。
xとなるようなものなので、
図-3以外にはあり得ません。
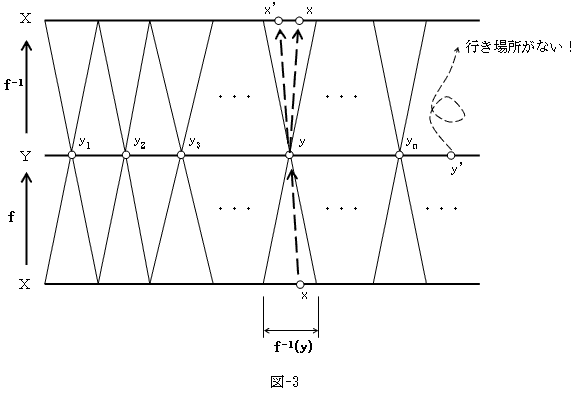
図-3には、二つ問題があります。まずy=f(x)である時、
f-1(y)=xと決める事は出来ますが、逆像f-1(y)の中にもう一点x'(x'≠x)が含まれた場合、
f-1(y)=x'でもあるとせざる得ません。これはy=x2について逆関数を考えようとした場合、
x=±y1/2となってしまうような、良くある話で、写像の定義に反します(同じxに2つのyが対応するので)。
従って逆像f-1(y)は、f-1(y)={x}の一点集合である必要があります。定義4-1.に戻れば、
これはfが単射でなければならない、という事です。
もう一つは、f(X)≠Yである事です。fが単射であっても、f(X)≠Yならば、
f(X)の外にあるy'に対しては、f:y'  xとなるxがありません。このような場合、
「ただし、y'がf(X)に属さない時は、逆写像を考えない」などと但し書きを付ける手はありますが、
但し書きには一般性がありません(忘れるかもしれない)。
xとなるxがありません。このような場合、
「ただし、y'がf(X)に属さない時は、逆写像を考えない」などと但し書きを付ける手はありますが、
但し書きには一般性がありません(忘れるかもしれない)。
このような定義としての曖昧さを除くために、写像の定義では、任意のx∈Xには、
必ず対応するyがなければならない、という制限を設けています。よってfは、全射でなければなりません。
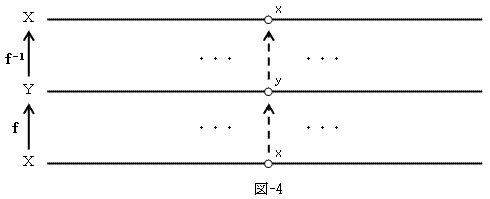
fは単射かつ全射でなければならないので、双射です。逆にfが双射なら、図-3は図-4にようになるので、
f-1:y  xとなる逆写像f-1は、常に存在します。
xとなる逆写像f-1は、常に存在します。
しかし同時に、次の事も言えます。
定理1.
f:X→Yが単射である時、値域をYからf(X)に移行する事によって得られる写像f':X→f(X)は、逆写像f '-1を持つ。
f:X→Yが全射である時、各y∈Yに対して、一点x∈f-1(y)を集めて作ったXの部分集合を、
A={x∈X|xはf-1(y)に属するどれか一点で、y∈Y}
とする。fのAへの制限f ':A→Yは、逆写像f '-1を持つ。
f:X→Yである時、各y∈f(X)に対して、一点x∈f-1(y)を集めて作ったXの部分集合を、
A={x∈X|xはf-1(y)に属するどれか一点で、y∈f(X)}
とする。定義域をXからAへ、値域をYからf(X)へ移行する事によって得られる
写像f':A→f(X)は、逆写像f '-1を持つ。
[証明]
いずれもf 'は双射だから。
[証明終]
制限や移行の「意」はわかって頂けるものと想像します。
制限(縮小)に対して延長(拡大)という用語もあります。
延長とは、もとの定義域を含むように、定義域の集合を任意に大きくする事です。
以上が、自由な定義域,値域の拡縮、すなわち「部分写像」の例です。
6.合成写像
合成写像は合成関数と同じです。f:X→Y,g:Y→Zであるとき、x∈X,y∈Y,z∈Zとして、写像、
x  y
y  z
z
を合成写像と言い、g  f:X→Y→Zと書きます。ふつうに書けば、z=g(y)=g(f(x))です。
f:X→Y→Zと書きます。ふつうに書けば、z=g(y)=g(f(x))です。
自分は一応、数値計算分野の出身ですが、実務計算において合成写像の必要性を感じた事は、ほとんどありません。
写像の合成の概念は、やはり理論を読み易くするためにあると思えます。
写像の合成は、意味をはっきりさせるために写像を分解したり、二通りに写像の意味を解釈したい場合などに利用されます。
例えば、写像(x1,x2,・・・,xk,・・・xn)
 f(xk)を考えてみます。
f(xk)を考えてみます。
ここで(x1,x2,・・・,xk,・・・xn)は、
積集合X1×X2×・・・×Xnの一点を表わします。
積集合の代表例は、2次元平面R2=R×Rです。この場合の一点は、
(x1,x2)∈R×R=R2
となります。
積集合X1×X2×・・・×Xnは大抵、Πi∈IXiと略記されます。
形式的には、Σi∈IXi
=X1+X2+・・・+Xnと同じです。ここで何故、添え字がi∈Iかと言うと、
添え字i=1,2,・・・は必ずしも数字でなくても良いからです。とにかくi≠jのとき、
Xi≠Xjと区別できれば良いので、Xα≠Xβでも良いわけです。
Σi∈{ギリシャ文字の集合}Xi,Πi∈{ギリシャ文字の集合}Xi
というわけです。良く利用されるのが、Σi∈Naiです(Nは自然数全体の集合)。これは、
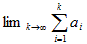
と同じです。ざっくり言えば、N={1,2,・・・,i,・・・,∞}と思っても良いからです(本当は、∞はNに属しませんが)。
ところで、写像(x1,x2,・・・,xk,
・・・xn)  f(xk)は、
写像g:xk
f(xk)は、
写像g:xk  f(xk)と実質的に同じです。何故なら関数値f(xk)が、
xkだけで決まるからです。このような事をはっきりさせるために、射影prkを用意します。
f(xk)と実質的に同じです。何故なら関数値f(xk)が、
xkだけで決まるからです。このような事をはっきりさせるために、射影prkを用意します。
「pr」はprojection(プロジェクション,射影)の意味です。
さらに(x1,x2,・・・,xk,・・・xn)を略記して、
(xi)と書きます。射影prkとは、
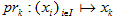
で定義される写像です。これを用いると、先の写像fは、
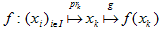
と分解され、f=g  prkである事から、fが実質的にgだけで定まる事がはっきりします。
二通りに写像の意味を解釈したい場合として、三角関数の加法定理を挙げます。
prkである事から、fが実質的にgだけで定まる事がはっきりします。
二通りに写像の意味を解釈したい場合として、三角関数の加法定理を挙げます。
2次元平面における回転行列T(θ)がわかっているとします。最初にベクトル(x,y)をα回転させて(x',y')を得、
その後に(x',y')をβ回転させて(x",y")を得る操作は、ベクトル(x,y)を一気に(α+β)回転させて(x",y")を
得る操作と同等です。写像の言葉で書けば、
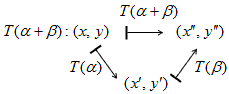
となりますが、行列記法の信じられないくらいの出来の良さから、
回転の1次変換の合成は行列の積になるのが最初からわかっています。従ってこの「図」より、
T(α+β)=T(β)T(α)が導かれ、結果は、お馴染みの加法定理になります。
この例のように、写像の意味を二通りに解釈して結果が同じである事に注意すると、
面倒な計算や考察がほとんど抜きになる、びっくりするほど簡潔な証明が得られる場合が、
けっこうあります(幾何的証明と比較してみて下さい)。
写像の合成を利用する理由は、もう一つあります。それは、写像に関する性質を定義2〜4のような
集合の言葉ではなくて、写像の言葉として定式化すると、驚くほどスマートな証明が得られる場合もあるからです。
集合XからXへの恒等写像、すなわちIdX:X→Xを、x  xで定義します。
xで定義します。
定義5.(左逆写像,右逆写像)
f:X→Yとする。r:Y→Xが、r  f=IdXとなる時、rをfの左逆写像(引き込み)と言う。
f=IdXとなる時、rをfの左逆写像(引き込み)と言う。
f:X→Yとする。s:Y→Xが、f  s=IdYとなる時、sをfの右逆写像(押し出し,切口)と言う。
s=IdYとなる時、sをfの右逆写像(押し出し,切口)と言う。
定義5.については、次の基本定理があります。
定理2.(単射,全射の判定条件)
f:X→Yとする。fが左逆写像rを持てば、fは単射である。
f:X→Yとする。fが右逆写像sを持てば、fは全射である。
定理2.は証明しませんが、図-3のイメージを持てれば、定理2.はほとんど自明です。
定理2.の応用(系)として、次の定理3.を挙げます。
定理3.
f:X→Yとする。写像g:x  (x,f(x))は双射である。言い換えれば、写像fのグラフGをX×Yの部分集合として、
G={(x,y)∈X×Y|y=f(x)}で定義したとき、写像g:X→Gは双射。
(x,f(x))は双射である。言い換えれば、写像fのグラフGをX×Yの部分集合として、
G={(x,y)∈X×Y|y=f(x)}で定義したとき、写像g:X→Gは双射。
[証明]
もちろんベタな証明も可能ですが、ここでは定理2.を用いてみます。
gが双射である事を言うためには、単射かつ全射である事を言えば良いわけです。
定理2.によればそれは、左右逆写像がある事と同じです。
r:(x,f(x))  xと定義する。これは写像である。何故なら、全ての(x,f(x))∈Gでこれは定義でき、
(x,f(x))を一つ定めれば、xは一つだけ定まるから。
xと定義する。これは写像である。何故なら、全ての(x,f(x))∈Gでこれは定義でき、
(x,f(x))を一つ定めれば、xは一つだけ定まるから。
s:(x,f(x))  xと定義する。これは写像である。何故なら、全ての(x,f(x))∈Gでこれは定義でき、
(x,f(x))を一つ定めれば、xは一つだけ定まるから。
xと定義する。これは写像である。何故なら、全ての(x,f(x))∈Gでこれは定義でき、
(x,f(x))を一つ定めれば、xは一つだけ定まるから。
r  f:x
f:x  (x,f(x))
(x,f(x))  xであり、これはr
xであり、これはr  f=IdXを意味する。
f=IdXを意味する。
f  s:(x,f(x))
s:(x,f(x))  x
x  (x,f(x))であり、
これはf
(x,f(x))であり、
これはf  s=IdGを意味する。
s=IdGを意味する。
以上より、写像g:X→Gは全射かつ全射なので、双射である。
[証明終]
定理3.の一つの結果として、任意の写像のグラフは、必ずパラメータ表示を持つ事が言えます。
定理4.(パラメータ表示の存在)
f:X→Yとする。双射h:T→Xが存在すれば、t∈T,x∈X,y∈Yかつy=f(x)として、
(x(t),y(t))∈Gは、fのtによるパラメータ表示である。
[証明]
写像g、
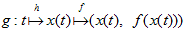
を考えれば、y=f(x)から、(x(t),f(x(t)))=(x(t),y(t))∈G。
従って定理3.よりfは双射。hも双射だから、g=f  hは双射(双射の合成が双射は、ほぼ明らかと思います。
例えば図-4)で、g:T→G。これはgが、fのtによるパラメータ表示である事を意味する。
hは双射(双射の合成が双射は、ほぼ明らかと思います。
例えば図-4)で、g:T→G。これはgが、fのtによるパラメータ表示である事を意味する。
[証明終]
またほぼ自明な結果ですが、次も導けます。f:X→Yが逆写像f-1を持てば、
f-1  f=IdX,
f
f=IdX,
f  f-1=IdYなので、
fとf-1は互いに互いの左右逆写像になっている。
従って、fとf-1はどちらも双射。
f-1=IdYなので、
fとf-1は互いに互いの左右逆写像になっている。
従って、fとf-1はどちらも双射。
大学の数学と高校数学の大きな違いは、物事の定式化(定義の仕方)です。大学の数学の定式化は、
高校よりもずっと抽象度が高くなっています。それは大学の数学が、実務重視、計算主体の高校数学から、
一般性を重視した定性論に移行するからです。理論は概念主体となり、上で見たように数字を使った計算は、
ほとんどなくなり、見慣れぬ記号と論証が飛び交って、最初はどうしても戸惑います。
しかしこれらは、とうに経験済みの事でもあります。小学校の算数から中学校の数学に上がった時、
具体的な数値計算3×(2+1)は、文字式の計算a(b+c)に抽象化されます。
中学校から高校に上がった時には、例えば漸化式an+1=an+(n−1)なんかが出てきます。
漸化式は、高校以前には決して出てこない、再帰計算という新しい抽象概念です。
an+1=an+(n−1) ⇒ an=an-1+(n−2)なんて発想を平気で出来るようになるのには、
けっこう時間がかかったと思います(少なくとも自分はかかりました)。
それ以外にも、因数分解のシステム化,2次不等式,剰余定理,対数/指数,1次変換,関数などなど、
考えてみれば、新しい抽象概念のオンパレードです。
実際そのために、「高校数学の壁」を越えられない人もいます
(私の息子がそうです。理数系の高校にだったのに、音大へ行きました)。
「大学数学の壁」は「高校数学の壁」より高いです。それは抽象度が、以前とは比較にならない程大きく上がり、
それを前提にした「数学の組織化」が本格的に始まるからです。しかし、少なくとも大学初年級の段階では、
高校数学を完成させる目的で、新しい概念は投入されて行きます。その意味では、高校との連続性はありますし、
しかも一度は経験した事です。とは言うものの、大学は専門職を養成する場です。
辛い部分はきっとあると思います。自分もけっこう苦労しましたが、ここで「けつまづく」のは、勿体無い気がします。
7.同型
集合と構造と写像,写像の単射,全射の概念が結びついて、同型の概念が出てきます。
ここでは2次元平面の位置ベクトルを取り上げます。
集合とは物の集まりの事で、物は何でもOK、でした。
そこで、2次元平面の位置ベクトル全体の集合Vを、考えます。
Vは、2次元平面の位置ベクトルを全部集めたもので、無限個の要素を持ちますが、
例によって、「集まったと思った」瞬間に、Vは存在しているものと考えます。
Vの要素には演算が定義されています。a,b∈Vとすれば、a+bも位置ベクトルなので(ふつうの意味で)、
a+b∈Vです。αを実数とすれば、αaも位置ベクトルなので、αa∈Vです。
また、a+b=b+a,αa=aα,a−a=0(0ベクトル),0a=0(左辺の0は実数の0,右辺は0ベクトル)なども成り立ちます。
つまり集合Vは、最初から構造を持っていると考えられます
(厳密には、集めた後に構造を入れているのですが、そこは省略します)。
位置ベクトルに成り立つ演算を持つ集合は、線形構造を持つと言い、
Vのことを線形空間(ベクトル空間)と名付けます。それで、Vの要素はベクトルと呼ばれます。
しかし、たんに線形構造を考えただけでは、その構造は絵に描いた餅なのです。
現実には、もっと実務に役立つような内部構造が必要です。構造は、部分集合を集める条件によって発生する、と述べました。
この場合の部分集合は、「基底」と呼ばれるもので、「基底」の集め方を与える事によって、新しい構造が発生します。
新しい構造とは「次元」です。Vは2次元平面の位置ベクトルを集めたものなので、「Vが2次元のベクトル空間である」
事の道筋を概略示すのが、ここでの目的です。
最初に、ベクトルの独立,従属の概念を定義します。
定義6.(ベクトルの独立,従属)
Vをベクトル空間とする。a1,a2,・・・,an∈V、
k1,k2,・・・knを実数とする。
k1a1+k2a2+・・・+knan=0
⇒ k1=k2=・・・=kn=0
が成り立つとき、ベクトル空間のベクトルを集めた、
部分集合{a1,a2,・・・,an}は、独立と言う。
そうではない時、すなわち、
k1a1+k2a2+・・・+knan=0
であっても、どれかのkiがki≠0になれるとき、
ベクトル集合{a1,a2,・・・,an}は、従属と言う。
従属なベクトル集合の例は、2次元平面の位置ベクトルを集めたVから、
任意に3本のベクトルa1,a2,a3を拾って作った{a1,a2,a3}です。
実際、a1=(x1,y1),a2=(x2,y2),
a3=(x3,y3)とすれば、
k1a1+k2a2+k3a3=0は、
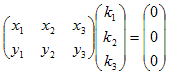 (1)
(1)
となり、条件数<未知数の数なので、常に0でないk1,k2,k3が可能です。
任意の3本以上のベクトル集合でも、同じ状況が成り立つ事がわかります。
次に2本のベクトルを拾った場合は、少し状況が違います。
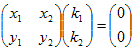 (2)
(2)
です。x1y2−x2y1≠0であれば逆行列があるので、
k1=k2=0であり、x1y2−x2y1=0なら、
k1=k2=0とは限りません。
すなわち、a1とa2が平行でなければ{a1,a2}は独立で、
a1とa2が平行なら{a1,a2}は従属です
(実際には位置ベクトルなので、a1とa2は、同一直線状にある)。
1本の場合はどうでしょう?。ka=0です。
a≠0ならk=0でなければならず、a=0ならk≠0でもOK (3)
以上の状況は、じつは当然でもあります。(2)のa1,a2を、座標軸に平行なベクトルとみなせば、
3本目のa3は常に、a3のa1とa2への射影ベクトルによって分解できて、
a3=k1a1+k2a2と表わせるので
(ベクトルの平行四辺形合成則)、移項すれば、
−k1a1−k2a2+1・a3=0
となり、{a1,a2,a3}は必ず従属で、
(k1,k2)はa3に対して一意に定まる事もわかります
(3本以上でも同様)。
そして座標軸に平行なベクトルは、互いに必ず平行ではありません。
この場合の座標軸には、任意に回転した直交座標系や、任意の斜交座標系も許されます。
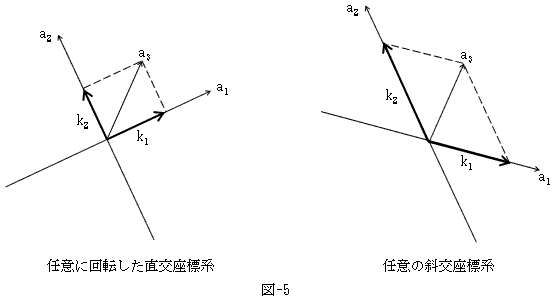
ところが上記の事態は、じつは定義6.の中に含まれています。
何故なら、ベクトル集合{a1,a2,・・・,an}が従属なら、
どれかのkiは0でないので、k1a1+k2a2+・・・+knan=0は、
ai=−k1/ki・a1−k2/ki・a2−
・・・−ki-1/ki・ai-1−ki+1/ki・ai+1・・・−kn/ki・an
と変形できます。さらに{a1,a2,・・・,ai-1,ai+1,・・・,an}が独立であれば、
aiの分解が一意である事も示せます。何故なら、
ai=−k1/ki・a1−k2/ki・a2−・・・−ki-1/ki・ai-1−ki+1/ki・ai+1・・・−kn/ki・an
ai=β1a1+β2a2+・・・+βi-1a i-1+βi+1a i+1・・・+βnan
と二通りの分解があった時には、辺々等置する事により、
(β1+k1/ki)a1+(β2+k2/ki)a2+・・・+(βi-1+ki-1/ki)a i-1+(βi+1+ki+1/ki)ai+1+・・・=0
であり、{a1,a2,・・・,ai-1,ai+1,・・・,an}が独立である事から、
定義6.より、任意のj≠iかつj=1〜nについて、βj+kj/ki=0、すなわちβj=−kj/kiとなって、
分解の一意性も示せるからです。
定義6.は、2次元の位置ベクトルに対して成り立つ事実を、非常に間接的で遠まわしな方法ではありますが、
とにかく再現しています。定義6.には、たった一つだけ利点があります。
それは、任意次元の位置ベクトルに対しても同じ言い方が出来る、という利点です。
それは3次元の位置ベクトル全体の集合Vを考えてみれば、すぐわかると思います。
ところで、2次元の位置ベクトルに関して、3本以上のベクトル集合は常に従属であり、
2本以下のベクトル集合は、独立または従属であるという事実に普遍性がある事には、すぐ気づけます。
例えば、2次元の位置ベクトルではなく、2次元の矢線ベクトル全体の集合V'を考えてみても、
同じ状況が成り立つのはすぐわかります。さらに{a1,a2}を、座標軸に平行なベクトルに取れる事も注意しましたが、
この場合の座標系には、任意の直交座標や斜交座標もOKです。すなわち2次元であれば、
3本以上のベクトルは常に従属で、2本以下のベクトル集合は、独立または従属であるという事実には、
座標系に依存しないという普遍性もあります。
このような発想から、「基底」の概念が現れます。まず次の定理が一般的に導けます。
定理5.
ベクトル空間から取れる、独立なベクトル集合の最大本数は、取り方によらず一定である。
定理5.は証明しませんが、本質的には(1),(2),(3)の計算を行います。この定理の結果をもとに、普遍性を意識した、次の「基底」の定義が生まれます。
定義7.(基底の定義)
ベクトル空間から独立に取れる最大本数のベクトルを集めた、ベクトル空間の部分集合を、基底と言う。
基底とは、座標軸に平行なベクトルを集めたものと本質的に同義です。座標軸の本数とは、その空間の次元です。よって次の普遍的定義になります。
定義8.(次元)
ベクトル空間Vの基底の本数を、次元と言い、dim(V)で表わす。
さて、以上の背景の基に、次の関係式を考えます。ベクトル空間Vから、その要素vを一つ持ってきて、
それをVの基底{a1,a2,・・・,an}によって分解します。
v=β1a1+β2a2+・・・+βnan (4)
です。この基底表現(分解)は、vに対して一意的なものでした。
さらに基底{a2,a2,・・・,an}の本数は、定理5.から、
その選び方によらず常に、次元nです。(4)の最も簡単な例は、やはりここでも、2次元の位置ベクトルになります。
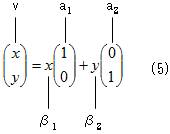 (5)
(5)
ここで(4)や(5)において、vをVの任意のベクトルだとしてみると、(β1,β2,・・・,βn)や(x,y)は、
任意の実数の範囲を動きます。逆に(4)や(5)で、(β1,β2,・・・,βn)と(x,y)が、
任意実数の範囲を動けば、vはVの任意のベクトルを表わす事もわかります。
しかも基底の本数nは、任意に動く(β1,β2,・・・,βn)や(x,y)に関わらず、常に一定です
((5)では、n=2に固定)。そして図-5を思い出すと、(4)や(5)は、ベクトル空間の作り方、
すなわち次元構造の具体化だと了解できます(図-6)。この事を、
基底{ai}は、ベクトル空間Vを「張る」(またはVの「生成系」).
と言い表します。またもや、図形的直感(イメージ)を反映した用語の導入です。
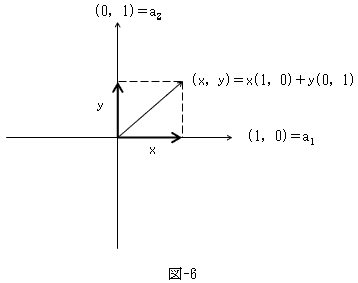
ところが、式(5)と図-6を比較してみると、式(5)自体が図-6に対する、一種の概念図になっている事がわかります。
だってやってる事は、いっしょじゃないですか!。
式(5)と図-6を、実際に意識して比較してみて下さい。意識する事は、次の一点に尽きます。
基底{ai}は独立なベクトルである。ただそれだけです。そのような事をイメージ付けるためにも、
「基底(座標軸)は、空間を張る」という用語が導入されます。
「式=概念図」という図式が成立する時、慣れは必要ですが、恐ろしく明快な定式化が実現できます。
何故なら、図形による直感的把握(定性性)と厳密性(定量性)を一挙に獲得できるからです。
この事を強調するために、式(5)のような書き方を使った、ベクトルに関する証明を「幾何学的」と称するくらいです。
以上の感覚を了解できれば、「同型」の概念は目前です。「同型」概念の定義(定式化)の動機付けを、
理解した事になるからです。
この観点から図-5を見直すと、図-6のような標準的座標軸(自然基底と言われます)であろうと、
任意の直交系でも斜交系でも、とにかくそれがn次元ならば、
v=k1b1+k2b2+・・・+knbn (6)
となるであろう事は、すぐだと思います。ここで{bi}は、n次元ベクトル空間の基底です。
(k1,k2,・・・,kn)は、任意の実数範囲を動きます。
もう一つ別の基底{ai}を考えた時、それに関しても同様に、
w=k1a1+k2a2+・・・+knan (7)
となります。ここで(6)と(7)の(k1,k2,・・・,kn)は、任意の実数範囲を動くので、
同じであってかまいません。そして(6)も(7)も、同じn次元のベクトル空間を作ります。
そうすると、次のような対応を考えてみたくなるのは、ほぼ必然と思えます。
v=k1・a1+k2・a2+・・・+kn・an
↓ ↓ ↓ ↓ (8)
w=k1・b1+k2・b2+・・・+kn・bn
(8)の左辺においては、v  wという対応であり、
右辺ではai
wという対応であり、
右辺ではai  biです。
つまり座標軸を別の座標軸に写すような対応です。
何故なら座標軸さえ定まれば、式(4),(5)より、ベクトル空間は発生するからです。
biです。
つまり座標軸を別の座標軸に写すような対応です。
何故なら座標軸さえ定まれば、式(4),(5)より、ベクトル空間は発生するからです。
しかもこの対応は、図-7より写像fとして定義できるのがわかります。それどころかfは、双射として定義できるはずです。
何故なら図-7では、(x,y)もvもwも、同じ2次元平面の一点を表わすので、
(k1,k2,・・・,kn)が任意である事を考慮すると、
一対一かつ上への写像が可能なのは、明らかだからです。
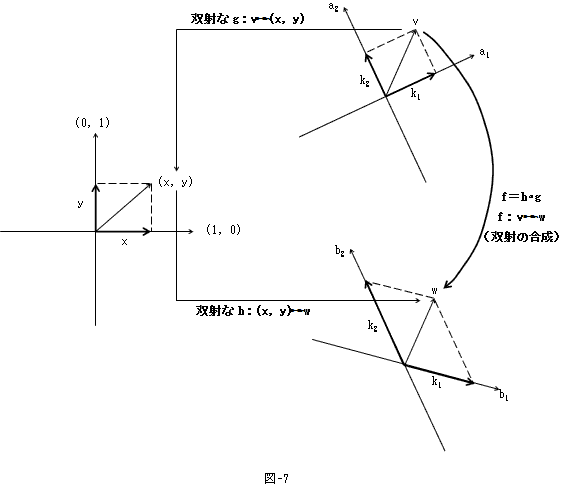
このようなfがあれば、次元構造は、位置ベクトルとか矢線ベクトルとかのベクトル空間の種類にも、
座標系の取り方にも依存しない、普遍構造である事がよりはっきりします。このためにこそ、fを考えます。
(8)において、w=f(v)と書いてみます。ベクトルvは、写像fによってwに移るという意味です。
しかし、(k1,k2,・・・,kn)は任意でした。
(k1,k2,・・・,kn)を適当に設定すれば、v=aiとも出来きます。
何故なら、基底ベクトルもベクトル空間の中の1本のベクトルに過ぎないからです。
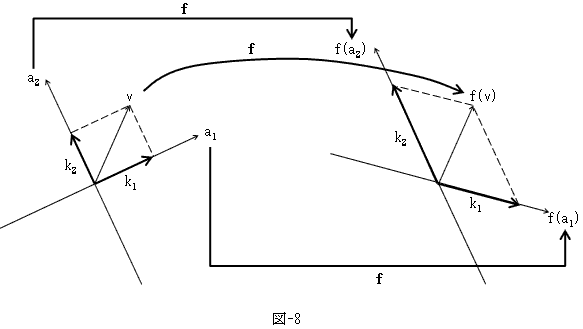
そうすると、bi=f(ai)でもなければなりません。それを絵にしたのが、図-8です。
図-8を、「定性性」と「定量性」が合体した、式(5)に載せます。
v= k1・a1 +k2・a2 +・・・ +kn・an
↓ ↓ ↓ ↓ (9)
f(v)=k1・f(a1)+k2・f(a2)+・・・+kn・f(an)
という事になります。
ところがここから、(9)の定量性能が発揮されます。
(9)の左辺に注目すると、v  f(v)です。左辺と右辺は「=」です。
従って、f(v)=f(k1・a1+k2・a2+・・・+kn・an)である事から、右辺に注目すると、
f(v)です。左辺と右辺は「=」です。
従って、f(v)=f(k1・a1+k2・a2+・・・+kn・an)である事から、右辺に注目すると、
f(k1・a1+k2・a2+・・・+kn・an)
=k1・f(a1)+k2・f(a2)+・・・+kn・f(an) (10)
でなければなりません。
(10)は結局、次の関係があれば良いと教えています。
定義9.(線形写像)
VとWをベクトル空間、f:V→Wとする。xとy∈V,kは実数として、
1) f(x+y)=f(x)+f(y).
2) f(k・x)=k・f(x).
が成り立つとき、ベクトル空間からベクトル空間への写像fを、線形写像と言う。
定義9.の1)と2)を満たすような都合の良い写像はあるのか?、という疑問はいちおう生じます。ところが、あるどころか殆ど自明なのです。
それが行列(一次変換)です。実際fとして行列Aを考え、xとyを(位置)ベクトルとすれば、
1) A(x+y)=Ax+Ay.
2) A(k・x)=k・Ax.
が成り立つのは、計算するまでもないと思います。
この節の冒頭で、「位置ベクトルに成り立つ演算を持つ集合は、線形構造を持つ」と述べました。「位置ベクトルに成り立つ演算」とは、
「+」と「スカラー倍」です。それが「線形構造を定義」します。
定義9.の1)と2)は、写像元から写像先へ、「+」と「スカラー倍」の関係を保存する、
すなわち「線形構造を保存する」のがわかります。このように、写像元から写像先へ、
写像元の要素間の関係を保存する写像を、「準同型写像」と言います。行列は、
「ベクトル空間の次元構造を保存しうる写像」です。このような写像を考えたくなる動機付けを与えたのは、式(5)です。
「準同型写像」が双射なとき、それは多くの場合「同型写像」になります。発想の原点は式(9)です。
式(9)の上下段どちらも、同じ「次元」のベクトル空間を作れるためには、上段における基底{ai}が、
下段においても基底{f(ai)}となる必要があります。
基底とは定義7.により、あるベクトル空間から取れる最大本数の独立なベクトル集合の事で、その本数を「空間」の次元と呼びます。
それが定義8.です。基底とは、座標軸に平行なベクトルを集めたのと、同義だからです。
あるベクトル空間から取れる独立なベクトルの本数は、取り方によらず常に一定です。それが定理5.です。
さらに、ベクトルの独立/従属の定義が、定義6.でした。
準同型写像である行列に、次の事が成り立つと、行列Aは同型写像になります。すごく綺麗な結果だと思います。

となります。さらに次元定理が成り立ちます。ここで次元定理とは、f=Aとした時、
dim(V)=dim(f(V))+dim(ker(f)) (12)
というもので、(12)のker(f)は、ker(f)={v∈V|f(v)=0}で定義されるVの部分空間です。
(11)と(12)は同値です。自分は、(11)と(12)の同値性が手に取るようにわかれば、
大学の初等線形代数の1/3は、制覇したと考えても良いと思っています。線形同型の正式な定義を挙げます。
定義10.(線形同型)
VとWをベクトル空間、f:V→Wとする。fがVの基底をWの基底へ双射に写すとき、これを線形同型と言う。
このときVとWも、同型(線形同型)と言われる。
つまり線形同型とは、座標軸を座標軸へ過不足なく写す写像なので、式(5)と定義9.、および(11)の冒頭を思い起こせば、
まさに「同じ次元型」を作るというわけです。有限次元ベクトル空間の構造とは、要するに「次元」と「基底」しかありません。
それは同型の定義10.を見ればわかります。逆に言うと、同型写像の定義を調べれば、その構造の本質がわかります。
定義10.には、図-6,7,8などと、ほぼ3重のイメージが重なっています。大学の数学とは、けっこうこんな感じです。
最後に一言。位置ベクトル「空間」と矢線ベクトル「空間」は、次元が同じなら同型になります。
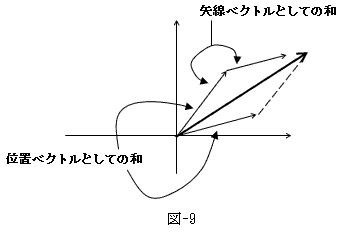
その状況を示したのが、図-9です。
図-9は、位置ベクトルの和も、矢線ベクトルの和も、結果は同じである事を示しています。
どうしてこんなに上手く行くのかと言うと、位置ベクトル「空間」と矢線ベクトル「空間」が「同型」だからです。
逆に、このような事を、言葉を最低限に切り詰めて言うために、「同型」という抽象的概念が導入されます。
大学では、もっとわかりにくい状況にも出会いますが、図-9の状況が同型に基づく事さえ了解できれば、次の事実は当然となります。
1)ふつう位置ベクトルと矢線ベクトルは、混用して用いるが、その結果は一致する。
2)何故なら、位置ベクトルと矢線ベクトルは同型になるように、注意深く定義されている。言い換えれば、そうになるように、作られたのだ。
3)従って、位置ベクトルと矢線ベクトルを混用して用いるのは、2つの理論が目論んだ正しい運用法である。
4)よって、位置ベクトルと矢線ベクトルは、是非とも混用して用いるべきだ(実際、便利です)。
大学において1)〜4)に相当するのが、関数空間と数ベクトル空間です。
無限次元である事をここで敢えてあっさり切り捨てれば、数ベクトル空間は普通の位置ベクトル空間に同型です。
という事は、関数空間は本質的に、位置ベクトル空間と考えて良い事になります。それがHilbert空間(ヒルベルト空間)です。
以上、勝手な事を書きました。
 x2などと書きますが、
事によったら、f:x
x2などと書きますが、
事によったら、f:x 
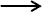 は、f:X→Yを表わし、
は、f:X→Yを表わし、 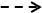 は、f:x
は、f:x  で表わした集合Xを隙間なく埋め、f(X)={y1,y2,y3,・・・,y,・・・}⊂Yは、
fが全射とは限らない事から一般には、f(X)≠Yである事もわかります。以上の事を念頭に置き、
逆写像(逆関数)f-1:Y→Xがあったとして、それが写像になる条件をさがします。
で表わした集合Xを隙間なく埋め、f(X)={y1,y2,y3,・・・,y,・・・}⊂Yは、
fが全射とは限らない事から一般には、f(X)≠Yである事もわかります。以上の事を念頭に置き、
逆写像(逆関数)f-1:Y→Xがあったとして、それが写像になる条件をさがします。



 f:X→Y→Zと書きます。ふつうに書けば、z=g(y)=g(f(x))です。
f:X→Y→Zと書きます。ふつうに書けば、z=g(y)=g(f(x))です。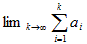
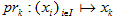
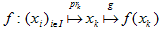
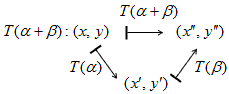
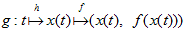
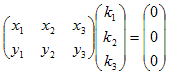 (1)
(1)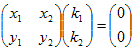 (2)
(2)
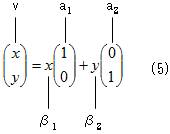 (5)
(5)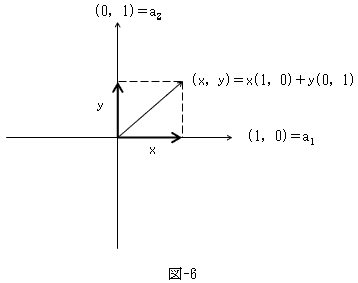





 BとDを結び、△ABD=a,△BCD=bとする。
BとDを結び、△ABD=a,△BCD=bとする。 まず、辺ADを垂直に二等分する直線をひく、(fig.1)
まず、辺ADを垂直に二等分する直線をひく、(fig.1)