NO.1740 最小公倍数 2008.9.15. 水の流れ
皆さん、今年の大分大学医学部の入試問題を改題して出題します。
注：この記事に関する投稿の掲載は、２００８年10月６日以降とします。
NO.1739 ページシステム(2) 2008.8.25 夜ふかしのつらいおじさん
XとYとの対戦で、XがYに勝つ確率をXｙで表すことにする。
すると、XとYとの対戦は、（Xｙ＋Yｘ）＝１と表せる。
１はどちらかが勝つという意味になる。
Ａｂ＝４／７、Ｂａ＝３／７、 Ａｃ＝２／３、Ｃａ＝１／３、 Ａｄ＝４／５、Ｄａ＝１／５
Ｂｃ＝３／５、Ｃｂ＝２／５、 Ｂｄ＝３／４、Ｄｂ＝１／４、 Ｃｄ＝２／３、Ｄｃ＝１／３
まず、AとB、CとDとの対戦は
（Aｂ＋Ba）・（Cｄ＋Dｃ）
＝Aｂ・Cｄ＋Aｂ・Dc＋Bａ・Ｃｄ＋Ｂａ・Ｄｃ
３位決定戦を考えると
＝Aｂ・Cｄ・（Ｂｃ＋Ｃｂ）＋Aｂ・Dc・（Ｂｄ＋Ｄｂ）＋Bａ・Ｃｄ・（Aｃ＋Ca）＋Ｂａ・Ｄｃ・（Ad＋Da）
＝Aｂ・Cｄ・Ｂｃ＋Aｂ・Cｄ・Ｃｂ＋Aｂ・Dc・Ｂｄ＋Aｂ・Dc・Ｄｂ＋Bａ・Ｃｄ・Aｃ＋Bａ・Ｃｄ・Ca＋Ｂａ・Ｄｃ・Ad＋Ｂａ・Ｄｃ・Da
決勝戦を考えると
＝ Aｂ・Cｄ・Ｂｃ・（Ab＋Ba）＋Aｂ・Cｄ・Ｃｂ・（Ac＋Ca）＋Aｂ・Dc・Ｂｄ・（Ab＋Ba）＋Aｂ・Dc・Ｄｂ・（Ad＋Da）
＋Bａ・Ｃｄ・Aｃ・（Ba＋Ab）＋Bａ・Ｃｄ・Ca・（Bc＋Cｂ）＋Ｂａ・Ｄｃ・Ad・（Ba＋Ab）＋Ｂａ・Ｄｃ・Da・（Bd＋Db）
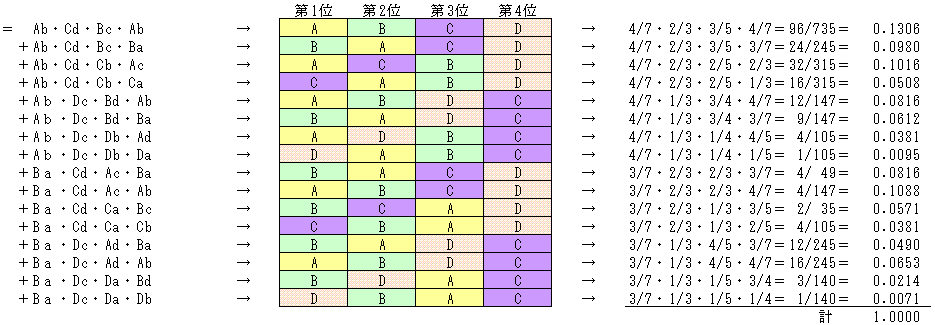
なお、メダル獲得の確率について、ＡとＢはページシステムの仕組みから１です。
ＣとＤは、初めの試合の勝者がメダル獲得の権利を得るので、Ｃは、Ｃｄと等しく２／３、ＤはＤｃと等しく１／３です。
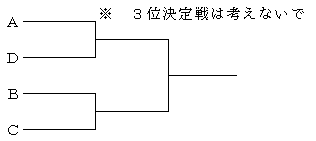さて、普通のトーナメントの場合を考えてみる。
予選リーグでＡＢＣＤの順番だと、ＡとＤ、ＢとＣの対戦になる。
まず、ＡとＤ、ＢとＣの対戦は
（Ａｄ＋Ｄａ）・（Ｂｃ＋Ｃｂ）
＝Ａｄ・Ｂｃ＋Ａｄ・Ｃｂ＋Ｄａ・Ｂｃ＋Ｄａ・Ｃｂ
決勝戦は
＝Ａｄ・Ｂｃ・（Ａｂ＋Ｂａ）＋Ａｄ・Ｃｂ・（Ａｃ＋Ｃａ）＋Ｄａ・Ｂｃ・（Ｄｂ＋Ｂｄ）＋Ｄａ・Ｃｂ・（Ｄｃ＋Ｃｄ）
表１と表２を比べると、予選で成績の良かったＡやＢの優勝の確率は、ページシステム方式の方が高くなっている。
逆に、予選で成績の悪かったＣやＤの優勝の確率は、低くなっている。
試合数が多くなれば実力のあるチームが有利になる。
