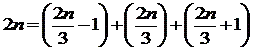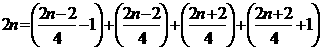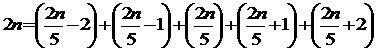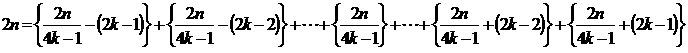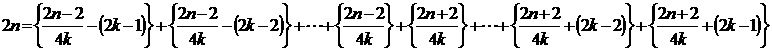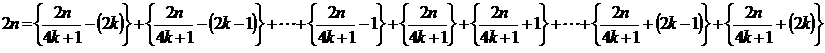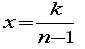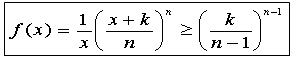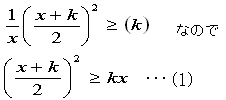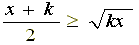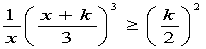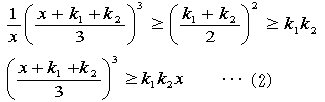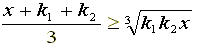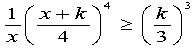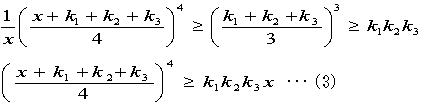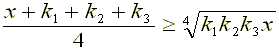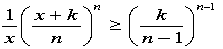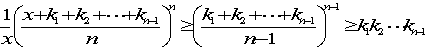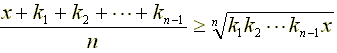NO.1737 ページスステム 2008.8.25 水の流れ
一部修正 8/25 22:00
第212回数学的な応募問題
皆さん、2008年北京オリンピックの女子ソフトボール競技決勝戦では、日本に
心から声援を送りました。悲願の優勝ができて感動を味わうことができました。
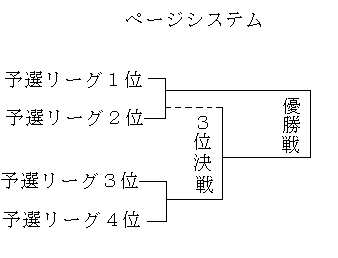
さて、ソフトボールで行われた決勝トーナメントですが、ページシステムという方法です。
予選リーグを行い上位4チームで行うものです。ここで、上位1位、2位は3位以内に入りメダルが確定します。
準決勝2試合は上位1位2位で戦い、勝ったら決勝戦進出します。 また、もう1試合は3位4位で負けたら、4位に確定します。
次に、1位2位の試合で負けたチームと3位4位の試合で勝ったチームが3位決定戦を行い、勝ったら決勝戦に進出、負けたら銅メダル決定となります。
最後にこの2チームで決勝戦を行い、金・銀メダルの争いをします。
ここで、問題を考えました。
予選リーグを行って上位4チームを決めますから、1位から4位のまでのチームの力に優劣ができます。
設定として、予選リーグ1位から4位までの勝つ力を4チーム全体で4割、3割、2割、1割とします。したがって、1位と2位が対戦した場合は1位が勝つ確率は4/7となります。
例えば、今回のように1位Aアメリカ、2位Bアメリカ、3位Cオーストラリア、4位Dカナダチームとします。
このとき、A、B、C、Dの4チームが金、銀、銅メダルのどれか1つを獲得する確率をそれぞれ求めよ。
注:この記事に関する投稿の掲載は、2008年9月15日以降とします。
NO.1736 連続する自然数の和(2) 2008.8.25 夜ふかしのつらいおじさん
ワーク1
36=22×32 なので、次の表より
36の約数の個数は9個
ワーク2
36の約数で奇数の個数は3個です。(1,3,9)
ワーク3
15=1×15=3×5 なので、次の式より
(a−k)+(a−k+1) +(a−k+2) +・・・+a +(a+1) +(a+2) +・・・+(a+k)
=a+a+a+・・・+a
=(2k+1)×a
15=15
15=4+5+6
15=1+2+3+4+5
ワーク4
2n+1=n+(n+1)
ワーク5
偶数2nについて
(1)連続する2個の自然数の和で表すことはできません
連続する2数は、奇数と偶数なので その和は奇数になります。
(2)連続する3個の自然数の和で表すことことができるのは、2nが6の倍数のときです。
6=1+2+3、12=3+4+5、18=5+6+7・・・
つまり
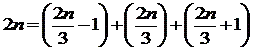
(3)連続する4個の自然数の和で表すことことができるのは、
2nが初項10、公差4の等差数列の項の値になるときです。
10=1+2+3+4、14=2+3+4+5、18=3+4+5+6・・・
つまり
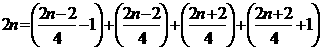
(4)連続する5個の自然数の和で表すことことができるのは、
2nが初項20、公差10の等差数列の項の値になるときです。
20=2+3+4+5+6、30=4+5+6+7+8、40=6+7+8+9+10・・・
つまり
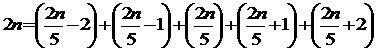
(5)連続する6個の自然数の和で表すことことことはできません。
連続する6数は3個の奇数、3個の偶数となるので、その和は奇数になります。
(6)4k−2個の和で表すことはできません。
連続する(4k−2)個の数は、2k−1個の奇数と2k−1個の偶数となるので、その和は奇数になります。
(7)4k−1個の和で表すことができるのは、2nが初項2k×(4k−1)、公差2×(4k−1)の等差数列の項の値になるときです。
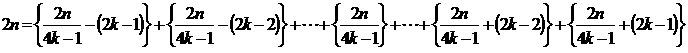
k=1のときは、2nとして {6,12,18,24,30,・・・}
k=2のときは、2nとして {28,42,56,70,84,・・・}
k=3のときは、2nとして {66,88,110,132,154,・・・}
k=4のときは、2nとして {120,150,180,210,240,・・・}
(8)4k個の和で表すことができるのは、2nが初項2k×(4k+1)、公差4kの等差数列の項の値になるときです。
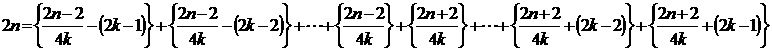
k=1のときは、2nとして {10,14,18,22,26,・・・}
k=2のときは、2nとして {36,44,52,60,68,・・・}
k=3のときは、2nとして {78,90,102,114,126,・・・}
k=4のときは、2nとして {136,152,168,184,200,・・・}
(9)4k+1個の和で表すことができるのは、2nが初項(2k+2)×(4k+1)、
公差2×(4k+1)の等差数列の項の値のときです。
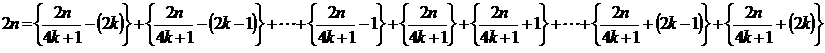
k=1のときは、2nとして {20,30,40,50,60,・・・}
k=2のときは、2nとして {54,72,90,108,126,・・・}
k=3のときは、2nとして {104,130,156,182,208,・・・}
k=4のときは、2nとして {170,204,238,272,306,・・・}
ワーク6
上の(7)から(9)に出てくる偶数を、小さい順に並べると、
{6,10,12,14,18,20,22,24,26,28,30,・・・}
出てこない偶数は
{2,4,8,16,・・・}
つまり、2kの形の数は、連続する自然数の和としては表せないようです。
64までの数で表現が1通りの数
6,10,14,22,26,34,46,68,62, ← 21×奇素数 の形
12,20,28,44,52, ← 22×奇素数 の形
24,40,56, ← 23×奇素数 の形
48, ← 24×奇素数 の形
64までの数で表現が2通りの数
18,50, ← 2×(奇素数)2 の形
36, ← 22×(奇素数)2 の形
64までの数で表現が3通りの数
30,42, ← 2×奇素数×奇素数 の形
60, ← 22×奇素数×奇素数 の形
54, ← 2×(奇素数)3 の形
ワーク7
ワーク3参照
ワーク8
奇数×奇数=【奇数】
偶数×奇数=【偶数】
偶数×偶数=【偶数】
ワーク9
15=1×15
=1+1+1+1+1+1+1+1+1+1+1+1+1+1+1
=(1-7)+(1-6)+(1-5)+(1-4)+(1-3)+(1-2)+(1-1)+1+(1+1)+(1+2)+(1+3)+(1+4)+(1+5)+(1+6)+(1+7)
−6から8までの連続する15個の整数の和になります。
ワーク10
36=36×1=12×3=4×9 なので
(1)36=36
(2)36=12+12+12=11+12+13
(3)36=4+4+4+4+4+4+4+4+4=0+1+2+3+4+5+6+7+8=1+2+3+4+5+6+7+8
ワーク11
3000=23×3×53 より
1000×3とみれば、
999+1000+1001
600×5とみれば、
598+599+600+601+602
200×15とみれば、
193+194+195+196+197+198+199+200+201+202+203+204+205+206+207
120×25とみれば、
108+109+110+111+112+113+114+115+116+117+118+119+120+
121+122+123+124+125+126+127+128+129+130+131+132
他は負の整数が混じるので省略します。
ワーク12
(1)Nが奇数ならば、ワーク4より連続する2数の和に直せます。
(2)Nが偶数ならば、素因数分解します。
その結果、奇数の因数がなければ、あきらめます。
N=n×(2k+1)となれば
N={n−k}×{n−(k−1)}×・・・{n−1}×{n}×{n+1}×・・・×{n+(k−1)}×{n+k}
とします。
また、4の倍数個の和で表すのならば、ワーク5の(8)を参照します。
NO.1735 虚構の近代 2008.8.10 DDT
次の本を読みました。
虚構の「近代」(科学人類学は警告する),ブルーノ・ラトゥール,新評論,2008/8/5(原著1991),川村久美子訳.
感想を言えば、信じられないくらい面白いものでした。恐らく難解な、この手の本としては珍しく、たった二日で読みました(訳わからなくても、読んで行ける)。
最初の印象は、理解社会学か知識社会学という印象でした。理解社会学と言えば、その開祖マックス・ウェーバーがいます。またその正統的継承者と言われる、バーガーもいます。
マックス・ウェーバーの「プロテスタンティズム倫理と資本主義の原理」は、ウェーバーの理解社会学の原点であり、そこでは資本主義のエートスとは、もともとどういうものであったのかに、焦点が当てられます。そこから資本主義というものの行動規範が、解明されて行きます。ここでエートスとは、動機付けとか熱意とか訳されています(タナトスの反対です)。
バーガーの「故郷喪失者達(近代化と日常意識)」では、近代化とともに始まった官僚制に焦点が当てられ、官僚制成立の結果としての、近代人(一般市民)の公人と私人の分離、あるいは官僚制の内面化による近代人の寄木細工性などが、ものの見事に語られます。
このような経験から、理解社会学の余り難しくない本(一般向けに書かれた本)は、けっこう好きでした。「虚構の「近代」」も一般向けに書かれた本です(でも難解?)。
そこではウェーバー流に言えば、近代を成立させたのエートスが語られます。近代とは何を目標にしたものだったのか?、です。しかしそこには、特異な構造が見られます。
(1)「科学/自然」と「社会/人間」と「神/人間」に関する三重のパラドックスおよび、三重のバランス.
(2)認識論による上記概念の純化(明確化)と実践の隠蔽(実際行動の不可視化).
です。ここで詳しくは言いませんが、上記が結局、近代主義の物質的な自由さ(無敵さ)と、非西欧社会に対する異常な侵略性を招いたというのです。
(3)近代主義の物質的な自由さ(無敵さ)とは、オゾンホールや温暖化や砂漠化に、直結する話です.
(4)非西欧社会に対する異常な侵略性とは、経済のグローバル化に直結する話です.
ラトゥールは、現在の世界情勢に直結する話をしています。それを「ベルリンの壁崩壊」という事件を期に書き上げた本書によって、予言しています。そして西欧社会には、恐らく現在の日本も含まれます。
彼によれば「ベルリンの壁崩壊」とは、西欧近代主義の終焉を暴いたものです。自由主義の勝利ではありません。何故ならマルクスの資本論とレーニン主義とは、西欧近代主義の一つの完成形だからです。不完全形である自由主義陣営も、いずれ立ち行かなくなるのは明らかだというわけです。その理由が(1)〜(4)です。こんなに面白い本は、久々に読みました。
理解社会学に話は戻りますが、その威力を思い知ったのは、比較的最近です。100年以上も前にウェーバーは、「職業としての学問(学問の価値自由性)」の中で、すでに次のように言っています。
全ての学問(科学)は、価値判断からは完全に自由である(自由でなければならない).それが証拠に学問は、人生について何も教えてくれないではないか.従って、ある価値を信じる者は、他者の信望する価値(宗教)の顔に泥を塗る者であり、その戦いを学問(科学)によって解消する事は決してできない。
我々学問の徒にできる事は、他者の価値を理解する事だけである。理解する事は、認める事とは決して違う。世界は、終わらない価値の争いの中にある.
このように、現実との間に異様な緊張関係を孕み、なおかつそれを許容し、苦闘する存在、それが認識の木の実を食べた、近代人なのである.
と悲観的意見を述べます(感動的な言葉ではありますが)。
間違いでしょうか?。現在の世界情勢を見る限り、ウェーバーの言った通りだと自分には思えます。イラン・イラク戦争,アフガンの情勢(ソ連、次にアメリカの介入),ミャンマーの現在とは、西欧と非西欧地域の宗教戦争なのだという意見を、自分は決して否定できません。
しかしブルーノ・ラトゥールの射程は恐らく、理解社会学の射程を越えています。非西欧社会に対して有効に機能していた比較文化人類学などは、西欧社会そのものへ、一度もまともに適用された試しはなかったし、また不可能であったと彼は言います。その理由が(1)〜(4)です。まともに適用できなかったものの中には、レヴィ・ストロースの構造人類学やウェーバーの理解社会学も含まれます。
「虚構の「近代」(科学人類学は警告する)」の副題「科学人類学」とは、科学的人類学ではありません。科学的人類学なら、レヴィ・ストロースなどが十分にやっています。「科学人類学」とは、西欧世界の科学活動を対象とした人類学的分析の事です。それが今まで不可能だったと彼は言います。そして驚くべき結論になります。
(5)近代世界など、一度も成立していなかった.
(6)我々は、我々自身を騙す虚構の中に住んでいる.
西欧世界の科学活動を、人類学や社会学の解析の俎上に載せられなかった事は、それ自体大問題です。何故なら西欧世界の科学活動とは、近代社会成立の大きな動機付け(エートス)であるからです。
ラトゥールとそのコミュニティーがそれらを実践すると、もともとは限定されていた科学人類学や科学社会学であったものが、通常の社会学,歴史学,人類学の射程を越えていきます。その理由も(1)〜(4)です。
しかしラトゥールが言い出すまで、近代主義の根本的な動作機構については、ほとんど気づかれていなかったわけです。そしてそこに気づけないために、温暖化や経済のグローバル化が生じたにも関わらず(地球規模の問題になったにも関わらず)、資本主義も共産・社会主義も、今やここまで手に負えなくなった問題を放置していた事になります。
帯にはこう書かれています。
人類の「今」を救う最高の座標軸.
と。これは嘘ではないと思います。
個人的に何故ここまでラトゥールが面白いかと言うと、自分は日本でのポストモダニズムの旗手の本を、けっこう丹念に読んだからです。
柄谷行人,浅田彰,増添大臣(現在),栗本伸一郎,上野千鶴子です。彼らの言説は一世を風靡したものの、どこかへ消えて行きました。実質的に生き残っているのは大臣だけでしょう(それも別の形で)。彼らは1990年代に出現した学会のトリックスター達でした。その言説が流行ったのは、やはりバブルという近代主義絶賛(ソ連は崩壊していた)の背景があったからだと思えます。
例えば浅田彰の代表作「構造と力」はとても面白い本でした。それはポスト構造主義とポストモダニズムを標榜していましたが、その結論は虚しいものでした。というか今にして思えば、結論らしい結論はなっかたのです。また結論を出さない事が、ポストモダンのカッコよさであり、それがポストモダンの価値でもあったと思えます。
今その理由がわかります。ブルーノ・ラトゥールを読んだせいです。ラトゥールは、ポストモダンを一刀両断に斬り捨てます。
最後に本書に寄せられた訳者の解説は、是非読むべきだと思います。本文を読む前でも後でも・・・。
本文を理解できないなら、解説を読んで比較対照しながら、本文を読み進むのは可能です。逆に本文を読み終わってから解説を読むと、感動的な解説である事がわかります。なぜ訳者が、このような解説を設ける気になったのか、その気持ちがわかります。訳者は、ラトゥールの現代社会に対する思いと熱意を、具体的に代弁しているのです。
NO.1734 連続する自然数の和 2008.8.4 水の流れ
第211回数学的な応募問題
皆さん、今回の問題は今年8月4日。5日に行われる「平成20年度 中学生高校見学会授業体験「数学」の問題です。
自然数1,2,3,4,5,6・・・の中には単位数1、素数2,3,5,・・・、
合成数4=2×2、6=2×3、・・・があります。
それでは本題に入る前に自然数の約数および約数の個数について考えましょう。
ワーク1:36を素因数分解して、その約数を全部書いてください。またその個数を求めてください。
ワーク2:36の約数の中で奇数は何個ありますか。
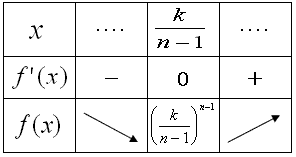
ここで、2+3=5,3+4+5=12,4+5+6+7=22、・・・のような和を連続する自然数の和という。
すなわち、最初の自然数をaとし、連続する自然数k個の和、
a+(a+1)+(a+2)+・・・+(a+k−1)をいいます。
ワーク3:15を連続する自然数の和で何通りにも表してください。
ワーク4:一般に、奇数2n+1を2個の連続する自然数の和で表してください。
ワーク5:では、偶数2nについては常に連続する自然数の和で表されますか、調べてください。
ワーク6:何か気がついたことはありませんか。
ヒント:どんな自然数でも連続する自然数の和で表されますか。
ヒント:ある自然数が連続する自然数の和で表されたとき、1通りですか。
次に、いくつかの連続する自然数の「ど真ん中」にある数を考えます。
例えば、4、5、6、7、8のときは「ど真ん中」は6です。
また、4、5、6、7、8、9のときは「ど真ん中」の数はありません。
したがって、連続する自然数の「ど真ん中」にある数は奇数とき存在して、偶数のときはありません。
ワーク7: 連続する自然数を2k+1個とし、「ど真ん中」の数をaとします。このとき、
(a−k)+(a−k+1) +(a−k+2) +・・・+a +(a+1) +(a+2) +・・・+(a+k)
を求めてください。
ワーク8:(奇数)×(奇数)=( )、(偶数)×(奇数)=( )、
(偶数)×(偶数)=( )の( )の中に奇数、偶数を入れてください。
ここで、15を連続する自然数の和で表したとき、何通りあるかを考えます。
最初に、15の素因数分解は15=3×5から、奇数の約数は1,3,5,15になる。
(1)「ど真ん中」を3としたとき、15÷3=5ですから、
15=3+3+3+3+3=(3−2)+(3−1)+3+(3+1)+(3+2)
=1+2+3+4+5 <完成>
(2)「ど真ん中」を5としたとき、15÷5=3ですから、
15=5+5+5=(5−1)+5+(5+1)=4+5+6 <完成>
(3)「ど真ん中」を15としたときは特殊な場合でして、連続する自然数が15という1個だけです。
ワーク9:(4)「ど真ん中」を1としたときを考えてください。
ワーク10:上のことを用いて36を連続する自然数の和で表してください。
ワーク11:では、3000を連続する自然数の和で表してください。
ワーク12:ある自然数Nを連続する自然数の和で表すときの方法をまとめてください。
注:この記事に関する投稿の掲載は、2008年8月25日以降とします。