| NO.1513 | 2005.2.4. | 佐野允信 | 三角形の形状(2) |
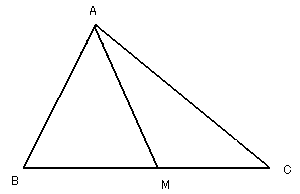
辺BC、CA、AB、AMの長さをそれぞれ a、b、c、dとする。
点Mは、辺BCの中点だから
BM=CM=(1/2)a ・・・(1)
∠MAC=αとおくと、条件より
∠BAM=2α ・・・(2)
△AMCにおいて、正弦定理より、

△ABMにおいて、正弦定理より
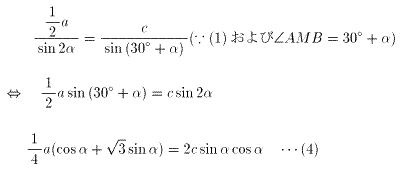
(1)より、△ABM=△AMCだから
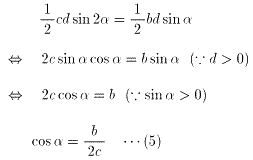
(3)、(5)を(4)に代入すると
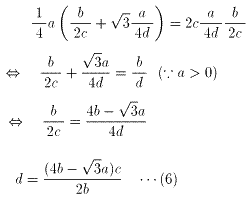
b>0 かつ c>0 かつ d>0より
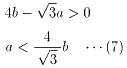
(1)より中線定理が成り立つので、 △ABCにおいて、余弦定理より (注) 下の図のような三角形です。
∠BAM=2θ、∠MAC=θ、AM=mとおきます。 先日NO.1491で、相当にかっとんだ事を書いてしまいましたので、お詫びに以下の本を紹介したいと思います。この本の出自だけは確かと思えますので、お詫びになってればと願うのですが・・・。 1.シュテルン・ゲルラハ実験 じつは電磁石において、電流の±のどっち側が、電磁石のN極になるかS極になるのか、忘れてしまいました。でも概念図としては、図-1でじゅうぶんです。電子はスピンすれば(自転すれば)、回転軸方向に極を持つ長さ0の棒磁石になります。で、シュテルン・ゲルラハ実験とは、次のようなものです。 2.電子のスピンモデルは本当に正しいのか? 3.実在とは何か? (1) (2) 4.EPR実験 5. ニールス・ボーアの反応 6. 不確定性原理 (3) (4) 図-2は、真空管の原型を少々変形したものです。まず高熱で温ためられた金属プレートであるカソードが、電子を放出します。これは熱電子効果といわれていて、完全に古典的現象です。そしてカソードと電位差が100Vあるプレート①が電子を加速します。しかしその先には、-200Vの電圧を持つプレート②が電子を待ち構えています。 7. EPR同時実験と「ボーアの裁定」の重み (5) (6) 8. 私にとっての量子力学 (強引ですね) (1)正20面体のハミルトン閉路(すべての頂点を一度だけ訪れて、元に戻る経
路)の個数を求めて下さい。 皆さんは、「コラッツ・角谷予想」をご存じでしょうか。現在のところ未解決のようです。これは次のことです。 このとき、次の問を考えてください。 問1:「操作数」1の整数、「操作数」2の整数を見つけてください。
問2:「操作数」nを持つ整数の個数をf(n)としたとき、f(3),f(4),f(5),f(6)を求めてください。
問3:f(n+2)をf(n+1)とf(n)との間に成り立つ漸化式を予想してください。
問4:問3の予想を証明してください。
問1:「操作数」1の整数は「2」、「操作数」2の整数は「4」 問2:f(3)=2 {3、8} 問3:f(n+2)=f(n+1)+f(n) 問4:f(n+2)個の数の中の偶数は2で割るとf(n+1)個の数のそれぞれの
数に一致し、f(n+2)個の数の中の奇数は1を加えて2で割るとf(n)個のそ
れぞれの数に一致するからです。
問1:a1=2,a2=4 問2: 問3:f(n+2)=f(n+1)+f(n) (n≧1) 問4: (証明終わり)
b2+c222
(6)を(8)に代入すると
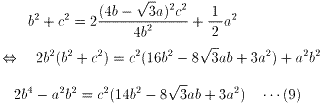
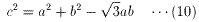
(10)を(9)に代入すると
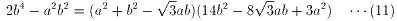
両辺をb4(≠0)で割り、
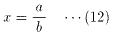
とおくと、
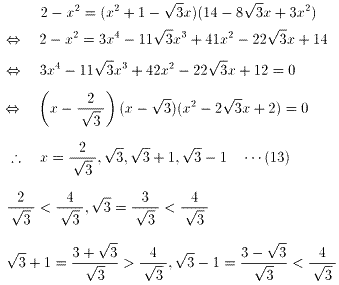
より、(7)を満たすものは、
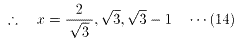
三角形の内角の和は、180゜だから、
3α+30゜<180゜
∴ α<50゜ ・・・(15)
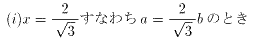
(10)より、
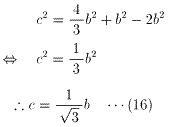
(16)を(6)に代入すると、
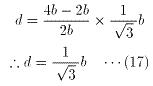
(17)を(3)に代入すると、
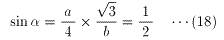
(16)を(5)に代入すると、
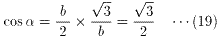
(18)、(19)より、
∴ α=30゜ ・・・(20)
これは、(15)を満たす。(20)より
∠BAC=3α=90゜゜ ・・・(21)
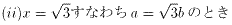
(10)より、
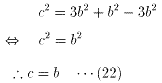
(22)を(6)に代入すると、
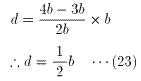
(23)を(3)に代入すると、
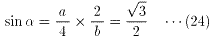
(23)を(5)に代入すると、
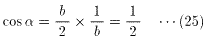
(24)、(25)より、
∴ α=60゜ ・・・(26)
これは、(15)を満たさない。
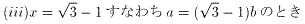
(10)より、
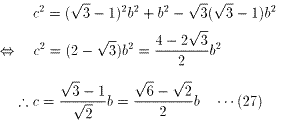
(27)を(6)に代入すると、
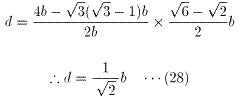
(28)を(3)に代入すると、
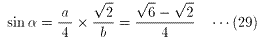
(27)を(5)に代入すると、
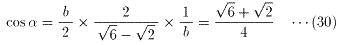
(29)、(30)より、
∴ α=15゜ ・・・(31)
これは、(15)を満たす。(31)より
∠BAC=3α=45゜ ・・・(32)
以上、(i)、(ii)、(iii)より、△ABCは、
∠BAC=45゜ または、∠BAC=90゜
の三角形である ・・・(答)
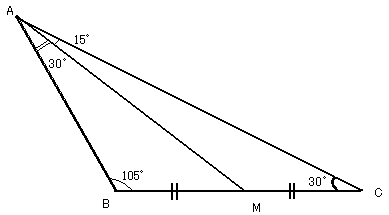
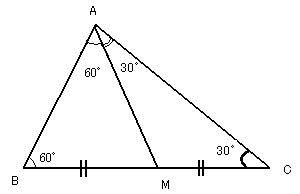
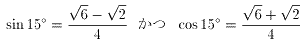
となる理由は以下の通り
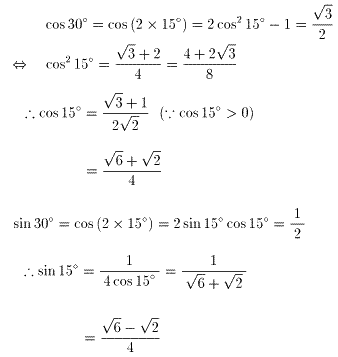

NO.1514
2005.2.4. 夜ふかしのつらいおじさん 三角形の形状(3)
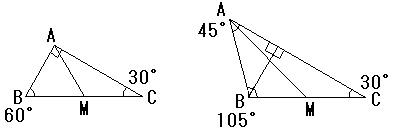
すると∠BAC=3θなので、∠ABM=150°-3θです。
△ABMにおいて正弦定理を用いると、
m/sin(150°-3θ)=(a/2)/sin2θ
△AMCにおいて正弦定理を用いると、
m/sin30°=(a/2)/sinθ
この二つの式からsin(150°-3θ)について解くと、
角を比較してsin(150°-3θ) =(sin30°・sin2θ)/sinθ
=((1/2)・2sinθcosθ)/sinθ
=cosθ
=sin(θ+90°) または sin(90°-θ)
150°-3θ=90°-θ または θ+90°
だから
θ=30° または 15°

NO.1515
2005.2.5. DDT 量子力学が思ったほど奇妙でないわけ(1)
種本は「量子力学の奇妙なところが思ったほど奇妙でないわけ,デヴィッド・リンドリー,青土社,1997年」です。この本の著者デヴィッド・リンドリーは、「ケンブリッジ大学で理論物理学を修了,フェルミ国立加速器研究所理論天体物理学部門研究員,ネイチャー誌編集員などを経て、現在サイエンス誌編集員」という輝かしい経歴を持つ人で(と本人が思ってるかどうかはしりませんが)、出自は確かと思えます。
ここでは個人的に特に興味のあったことだけをとりあげますが、もしも食指を喚起されたなら、是非原文を読んで下さい。「英語で!」。なぜなら訳が上手くはないからです。でも私は英語が読めません。すいません訳者の松浦先生。
ものの本によると、2個の完全に逆向きのスピンを持つ電子対を生成できるそうです。ここでスピンとは、球形ボールである電子の自転のことです。電子は電荷(電気)を持っています。電気(電荷)が回転すると、磁場を発生します。最もよくしられた例がコイルです。コイルは円筒状にぐるぐる巻きにされた電線のことで、そこに電流が走ると(電子が走ると)、その中に一方向の磁場できます。ぐるぐる巻きにされた電線の中を電子が走るとは、走っている電子にとっては、ぐるぐる回転するのと同じです。だから電子がぐるぐる自転すれば、それは棒磁石と同じです。ただし電子の棒磁石の長さは0です。それは、電子が点粒子と考えられているからです。直径0のボールという意味です。
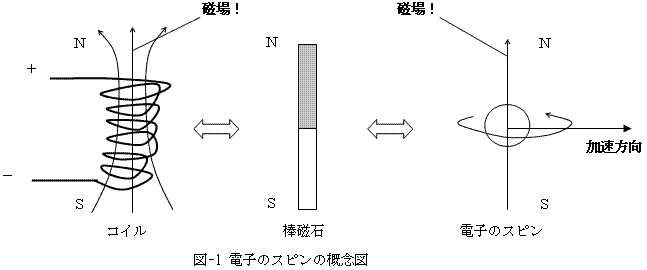
2個の完全に逆向きのスピンを持つ電子対を1組生成する(できるそうです)。その1組をスピンの回転軸とは直行方向に加速して電子線とする。これはブラウン管や真空管の原理でできます。そしてその電子線を、上下に極を持つ磁場の中を通します。スピンする電子は棒磁石なのだから、どちらかに曲がります。期待通り、1個の電子は上に行き、もう一方は下へ行きます。この実験の意味するところはこうです。1組の電子対の一方は上方向きのスピン軸成分を持ち、相方はその逆だった。ただし、どちらの電子が上方か下方かは、わからないので、その確率はそれぞれ50%となります。
しかしいったん、どちらが上方成分を持っていたか、下方成分を持っていたかがわかってしまえば、この結果は確認できます。上方へ曲がった電子線を、再び上下に極を持つ磁場の中を通すと、やはり上へ曲がり、相方はその逆です。電子の質量なんてカスみたいなもんですから、上下に極を持つ磁場の中を一回通った2個の電子は、上下磁場をくぐり抜けた後では、そのスピン軸を完全な上向きか下向きかに強制されたはずです。ということは、上下に分かれた電子線に左右の磁場をかけてみても無反応なはずです(長さ0の棒磁石!)。
ところが結果はそうなりません。1回目のシュテルン・ゲルラハ実験で上方へ曲がった電子線に、2回目のシュテルン・ゲルラハ実験として左右の磁場をかけると、今度は左か右に振れます。相方は正確にその逆で、どちらがどっちへ行くかは、再び50%の確率です。
上下磁場をくぐり抜けた後の電子は、スピン軸が完全に上向きか下向きかに揃っているはずである。よって、そのような電子線に左右磁場をかけても、電子線は曲がらないはずだ。にもかかわらず、電子線は今度は左右に50%の確率で曲がる。
このような事態を見たときに、まず真っ先に思いつくのは「電子のスピン(自転)モデルは本当に正しいの?」という疑問です。この疑問は、ある意味正しいことが知られています。詳しくは省略しますが、量子力学の言うところの電子のスピンには、アイソスピン(仮想自転と訳せます)というような、球形ボールをした電子の自転といった図-1みたいな単純で直接的なモデルでは、とても扱いきれないようなスピン量も存在するのは確かです。しかしなお、図-1と本質的には変わらないモデルを想定した多くの理論と、スピンに関する実際の観測とが一致するのも事実ですし、電子が他の物質と相互作用する場合に、多くの他の物質の理論(つまり電子の外部理論)と、スピン自転モデルが整合した結果を与え、実際の実験値を再現することも知られています。
このようなことから電子スピン・自転モデルは、もっと強調すれば「電子の自転という現象」は、実在するものと信じられています。ただし、ある意味で。ここからが問題です。
古典力学における、実在に関する暗黙の大前提は、次のようなものです。
「物理的実在は、その観測者と独立に存在する。
この観測者と独立に存在する物理的実在の諸性質のことを、アインシュタインは「物理的実在の要素」と呼びました。先のシュテルン・ゲルラハ実験は、古典力学的実在に関する暗黙の大前提と鋭く対立します。
従って、物理的実在の諸性質は観測者とは無関係に、いくらでも正確に測定できる」
まず電子のスピン方向は、アインシュタインのいうところの「物理的実在の要素」です。それは観測者と独立に測定できるものでなければいけません。しかし1回目のシュテルン・ゲルラハ実験で、上下方向にスピン軸が確定した電子対に、左右方向の2回目のシュテルン・ゲルラハ実験を行うと左右に振れるというのは、明らかに「古典力学の実在に関する大前提」に反しています。
何故なら、1組の電子のスピン軸が上向きか下向きかは、その生成時に決まっているはずです。そしてそれは、左右方向の2回目のシュテルン・ゲルラハ実験とは無関係に生成時に決まっているはずで、1回目の上下方向のシュテルン・ゲルラハ実験は、その上下方向の傾向を強調したにすぎず、完全に上下方向に強制された電子対は、左右方向の磁場には無反応でなければならないからです。だから、電子スピン・自転モデルは正しいのか?という疑いも当然生じるわけですが、2.で述べたように、これは相当念入りに実証された事実です。
では、どこがまずいのでしょう?。ボーアの答えはこうでした。ボーアとは、量子力学建設の最大の立役者の一人である、ニールス・ボーアその人です。ボーアはこう言います。
「物理的実在は、観測者と独立ではない。
これを、量子力学のコペンハーゲン解釈と言います。コペンハーゲンとは、ボーアのいた大学の所在地コペンハーゲンを記念して、そう言われているのですが、(2)は物理的な観測というものを、どう捉えるかという問題を含んでいます。1.からここまでで述べたように、それは相当に深刻です。最も原理的な問題としては「物理的実在は、観測者と独立ではない」という点です。それだけでなく、ボーアの言ったことを、そのまま信じれば「物理的実在そのものが無意味」になります。観測されるまで「物理的実在」は、あるのかないのかさえわからないだけでなく、(1)の意味で実在と呼びうるものも消失するかもしれないからです。ここから量子力学の観測問題が生じました。
もっと言えば、観測されないでも存在する物理的実在を想定することは、無意味である。
観測されたときに初めて、物理的実在と呼ばれるものが出現する」
さらに量子力学においては、全ての観測結果は「確率的」なのです。シュテルン・ゲルラハ実験が、その典型例です。これは次のEPR実験で述べますが、これも「物理的実在の諸性質は、いくらでも正確に測定できる」とした、古典力学の大前提に鋭く対立しています。
確率的観測および物理的実在の不定性、これを徹底的に考察したニールス・ボーアの考えは、観測問題の標準理論として、現在でも「ボーアの裁定」と言われています。ここで「裁定」とは、わかんないことは、みんなボーアのせいにしようというわけです(私が言ったわけじゃありません。デヴィッド・リンドリーがそう言ってます)。しかし(2)は、シュテルン・ゲルラハ実験を考えれば観測事実なのです。
ボーアのすばらしさは、この裁定に現れています。彼は、電子とか原子核とかの極微の世界において、我々が実際に行えることの限界を勇気をもって宣言し、なおかつそれが基礎理論(量子力学)と矛盾しないことを示しました。そして我々が実在と呼ぶものの根拠は、何をもってなのかを、反面教師的に暴いたのです。我々が常識的に実在と呼ぶものの根拠は、それが(1)です。そして(1)は観測事実によって否定されます。(1)の意味を反対側から徹底的に考察したと思われるボーアは、裁定(2)に辿り着きました。
このような観測事実を認めつつも、しかしなおかつ(2)の立場に、すばらしい頑固さと素直さで異を唱えたのは、やはりアルバート・アインシュタインでした。アインシュタインは、量子力学の成立期において光量子理論を唱え、量子力学の成立に多大な貢献をもたらした立役者の一人です。
現在では光子と呼ばれる光量子理論は、光電効果を説明するためにアインシュタインが考え出したものですが、その発想の原点は非常に常識的かつシンプルなものです。常識的で原理的な物理像を光電効果に適用したとき、マックスウェルの理論から波と考えられていた光は、じつは粒子の集団なのかも知れないとアインシュタインは気づきます。それはマックスウェルという当時の光の標準理論(じつは今でもそうです)からは、とうてい許容できない理論でした。しかし建設途上にあった量子論と関連する多くの実験事実は光量子理論支持し、彼はノーベル賞を得ます。
「物理的実在は、その観測者と独立に存在する」とか「物理的実在の諸性質は、原理的にいくらでも正確に測れる(当然確率的ではない)」とかは、常識的に考えれば当たり前の話です。それらが日常的に間違いなら、日常生活すらできません。
アインシュタインにはこのような、素直な原理が常にあります。その結果には「ボーアの裁定」のような気持ち悪さはありません。
アインシュタインは、もちろん「ボーアの裁定」を観測事実として認めていました。しかし「ボーアの裁定」が、物理的実在論の原理問題に発展することを、当時はっきりと言い放ったのは、アインシュタインただ一人でした。ボーアもこのことには当然気づいていましたが、彼は実在論として事を言い立てることを諦め(たのだと思います)、量子論の結果をどう受け入れるかという認識論として「裁定」を提出しました。
1935年、アインシュタインは二人の若い同僚、ポリス・ポドルスキー,ネーザン・ローゼンと供に、今日EPR実験と呼ばれる思考実験を提出し、量子力学が不完全であることを示そうとしました。EPRとは、3人の頭文字です。もともとのEPR実験は、反対方向に飛び出す光子の組について立論されたのですが、ここではデヴィット・ボーム(No.1491の「隠れたパラメータ理論」を創った人)がわかりやすく整理し直した、電子を使用するヴァージョンでいきます。
再びシュテルン・ゲルラハ実験を行います。ただし今度は、2個の電子は左右の反対方向に同じ速度で飛び出します。それぞれ左電子,右電子と呼んどきます。左電子が左へ1光年進んだところには、上下方向磁場が待ち構えています。左電子が磁場に達したときには、右電子は右へ1光年進むので、両者の相対距離は2光年です。
左電子が上下磁場で上へ曲がったとして、右電子が右へ1.5光年進んだときに、右電子に対して上下磁場の追試を行います。右電子は下へ曲がります。ここまでは、何の矛盾もありません。
スピンは保存量なので、一方が上向きなら、他方は当然下向きで、その方向は生成時に決まっているはずだからです。上に行くか下に曲がるかは50%の確率ですが、それは生成時の方向を、我々がたまたま知らなかったから確率になっただけで、スピン量そのものが、確率的に振る舞うわけではないと解釈できます。なんといっても、方向は生成時に決まっているはずだからです。右電子への追試結果が、それを支持します。
次に2回目のシュテルン・ゲルラハ実験を、左電子2光年の地点で、左右方向磁場でもって行います。1.で述べたように、意に反して左電子は、左右どちらかへ50%の確率で振れます。それが左なら、右2.5光年のところで行われた右電子への追試で、右電子は右へ振れます。
ここから得られる結論はこうです。まず観測のやり方によってスピン方向が決まるように思えます。であれば、それは生成時には決定されていないということです。よって、スピン量は本質的に確率的にしか測れないことになります。
次に、観測のやり方によってスピン方向が決まるのであれば、左電子が左1光年の地点で上下磁場に突入した瞬間に、瞬時に2光年という相対距離を越えて、その影響が右電子へ伝わったとしか思えません。1.5光年地点の右電子への追試がそれを支持します。そうでなければ、左2光年地点での左右磁場の影響が、4光年離れた右電子へ伝わり、右2.5光年地点での再追試を説明できないからです。これは、物理現象の非局所性を意味します。
それがどのようなものかは不明ですが、とにかく量子力学に従えば、瞬間的な情報伝達というものを認めざる得ないような事態になります。相対性理論によれば、光より速い情報伝達はありません。相対性理論を創ったのはアインシュタインその人です。彼が黙っていられるわけがありません。アインシュタインはこれを、
光より速い信号が必要なのは、
「例えば確率的にしか現象を説明できないところに、その不完全さが端的に現れている」
「物理的実在は、観測者と無関係に存在するのだ!」
つまりアインシュタインにとって、スピン方向はやはり電子の生成時に決まっています。しかし上下磁場,左右磁場の影響が数光年離れた電子間で伝わるのは、正しいと思われる(量子力学の計算結果は、実験を完璧に再現する)。よってその伝達を説明できるような、まっとうな物理機構があるはずだ。そのような物理機構があったとして、その効果はどんなものでしょう?
それは超光速の信号問題を解決します。超光速信号問題を解決できれば、観測の確率性も同時に解消されます。何故なら、上下,左右磁場の影響の伝達を因果的に説明できるので、観測のやり方によってスピン方向が変わるのは同じですが、スピン方向が観測されるまで不定ではないからです。スピン方向は、観測のあるなしに関らず常に確定したままで、観測の影響も、その伝達機構から決定論的に決まります。物理的実在も観測者と当然無関係に存在します。
従って、
アインシュタインは、このまっとうな物理機構をついに示せませんでした。けれど、彼のまっとうで素直で常識的な立論は、わかりにくいボーアの裁定に辟易していた多くの物理学者を引き付けます。その一人が、デヴィット・ボームでした。
デヴィット・ボームはその初期に、「ボーアの裁定」に含まれる「量子力学の認識論」を苦労して身につけ、世界的に有名な「観測理論の教科書」を書いたにもかかわらず、やはり「裁定」には納得できずアインシュタインと親交を結び、アインシュタインがEPR実験で提起した、まっとうな伝達機構の研究に向かいます。
それが「量子力学の隠れたパラメータ理論」です。デヴィット・ボームはある意味で、その非局所的伝達機構の完璧な数学的定式化に成功します。ここである意味でとは、どういう意味でしょう?
量子力学は基礎理論ではなかったにしても、現象理論としては完璧に実験を再現します。つまり「隠れたパラメータ理論」は量子力学と何一つ矛盾してはいけません。これがある意味での意味です。つまり、物理現象の非局所性と見えるものも、それは表現できなければなりません。
ところが、非局所的伝達機構に関するボームの数学的定式化は、それがどのような物理機構に対応するのか、誰にも説明できなかったのです。数学的定式化に対応する物理機構を誰一人思いつけないならば、物理現象の非局所性という説明不能な自然の性質を、逆に明示したと言えます。これは自然のクラスター性を信じるアインシュタインにとって、最も不満足な解答でした。
それでボームとアインシュタインの仲が悪くなったという事もないでしょうが、「隠れたパラメータ理論」の成功(?)は「アインシュタインの提起した伝達機構は、それが存在するにしても途轍もなく難しい問題である」ことを、多くの人々に印象づける結果になりました。これが「隠れたパラメータ理論」が、その後「鳴かず飛ばず」だった理由です。
しかし、ニールス・ボーアとアルバート・アインシュタイン、どちらが正しいのでしょう?。どちらも無視し得ない根拠があると思えます。結局は実験に頼るしかないのですが、だいたい、どのような実験をすれば良いのか?さえわかりません。この問題に応え得る実験を思いついた人は、ベルでした。
ベルについては次回に回すつもりなので、今回は、その後の経過と予備情報を紹介します。
EPR実験に対するニールス・ボーアの反応は、そっけないものでした。実際アインシュタインが言うところの非局所的伝達機構は、実証できる類のものではありません(現代の技術を使ったにしても)。
だから「気にするな!」というのがボーアの反応でした。
「自然は量子力学に従い、ボーアの裁定どおりに動く」
「そして伝達機構は見つからない」
たとえ「量子力学の隠れたパラメータ理論」が正しかったとしても、「隠れたパラメータ」は決してみつからないのです。何故なら、
からです。だからこその「隠れたパラメータ」です。
そして、
のです。これが観測事実です。
しかしニールス・ボーアは、アインシュタインの強力な反論に苦慮していました。アインシュタインとは正反対の立場で、量子力学的物質観が古典的実在論に矛盾することを、誰よりもわかっていたからです。
これは個人的感想ですが、ニールス・ボーアも本当は、アインシュタインと同様に明快な反論なり裁定なりをしたかったのではないか、と思います。EPR実験に対する彼の反応が、余りにもそっけなかったので、逆にそう思えます。
ニールス・ボーアは、アインシュタインが提起した実在論問題に対する明快な解答を出せないまま、没っしました。そして今でもこの問題には、最終的には決着が着いていません。ですが、少しずつ真実に向かって前進しているような気がします。特に種本である「量子力学の奇妙なところが思ったほど奇妙でないわけ」を読んでからは、そう思いました。
今まで2個の電子について、上下方向のスピンと左右方向のスピンが、互いに排他的であることを見てきましたが、何もこれはスピン量だけに限った話ではありません。また2個の電子(複数個の物体)に特有のことでもありません。
を不確定性原理と言います。その最も極端な例が、シュテルン・ゲルラハ実験における電子のスピン方向で、上下方向スピンと左右方向スピンの測定は完全に排他的で、どちらかを測ろうとする実験を行った瞬間に、他方の性質は完全に消えうせます。上下と左右の測定値は両立しません。そしてこれが、観測の確率性と、物理現象の非局所性をもたらすと思える実験事実でした。何故ならスピン方向は、観測のやり方によって決定されるからです。
一個の電子(1個の物体)についても、このような観測事実が存在します。ハイゼンベルグが提出したもともとの不確定性原理は、1個の電子の位置と運動量(速度)を測定する思考実験でした。
強調が多いことを許してください。量子力学は、実験や現実と何一つ矛盾しないくせに、日常感覚にはとことん歯向かいます。
ところでハイゼンベルグとは、量子力学の基礎方程式である行列力学を創った人です。シュレーディンガーは、それに対して波動方程式を創りましたが、両者の定式化が数学的に同等であることは、ファインマンが証明しました。
1個の電子の位置を測ろうとします。電子はとても小さな物体です。何せ「点粒子」ですから。電子は小さいので顕微鏡を使います。でもこの顕微鏡は、通常の光学顕微鏡では済みません。何故なら、光学顕微鏡はそこで使用される光の波長の長さ以下の物体は、捉えきれないからです。そこでγ線顕微鏡を使います。
γ線とは非常に波長の短い光で放射線と言われており、X線の親戚です。光量子理論によれば、光子は波長の長さに逆比例する運動量を持ちます。これを普通の言葉で言えば、光子は波長の長さに逆比例する衝撃力を持つということです。
従って電子の位置を無限に正確に測ろうとすればする程、ますます短い波長のγ線を使用せざる得なくなり、その結果、光子はますます強力な衝撃力で電子をキックします。ということは、位置測定後の電子の速度は、ますます皆目わからなくなります。
従って、
ことになります。これがハイゼンベルグの提出したオリジナルな不確定性原理です。どれくらい不正確かというと、位置の不正確さをΔx,運動量の不正確さをΔpとした場合、
程度です。ここでhはプランク定数で、量子力学に固有の定数であり、非常に小さいことが知られています。よって、考えている物体の運動量pが、とんでもない小さい値である場合にだけ、(4)は実際的な効果を発揮します。
例えば角砂糖の砂糖粒1個は十分に大きな物体で、それがあなたの鼻息で漂っていたとしても、十分大きな運動量を持ちます。何故なら砂糖粒1個の質量は、電子の数兆倍×数兆倍くらい大きく、それが鼻息程度の速度を持つということは、電子の平均的運動量の数億倍×数億倍以上の運動量となるからです。このような場合、(4)のプランク定数hは実質的に0とみなして良く、従って不確定性原理の効果は日常生活には決して現れません。これが、
理由の一つです。
しかし、このあたりが非常にわかりにくいのですが、ハイゼンベルグの思考実験は、我々が光学顕微鏡という手段しか使えないから、電子の位置と運動量(速度)を同時には正確に測れない、といっているわけではなのです。
量子力学を信じれば、それらは「どのような手段を使っても」同時には正確に測れません。ということは位置と運動量は、そもそも同時には確定し得ない「実在の要素」だということになります。それを量子力学という物理の基礎理論が保証します。
この効果は絶大です。何故なら物理の基礎理論が、位置と速度に不確定さを認め、もしも不確定性関係(4)が正しいのであれば、それは我々の観測とは無関係に常に成り立つからです。ほっとかれた電子に対しても、(4)が常時成立しΔxとΔpが確率的に変化するのであれば、位置と運動量(速度)は、本質的に確率的にしか測れないことになります。不確定性原理とは、量子力学の確率的性格を、定量的に表したものです。
これを支持する実験事実は、ごまんとあります。もしΔxとΔpが確率的に変化するなら、たまたまΔp=0となる瞬間もあるはずです。このときΔx=∞となります。これの意味するところは、「そのような瞬間には、電子はどこにでもいれる」ということです。漫画ちっくに言うと、
ことを意味します。トンネル効果とは、次のようなものです。
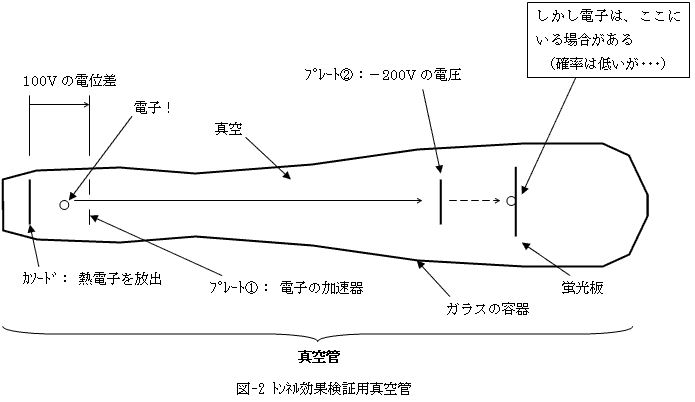
電圧とはポテンシャルエネルギーのことです。それは電荷を持った電子にとって、位置ポテンシャルエネルギーになります。よってカソードから発生し、プレート①で加速した電子は100V相当の運動エネルギーしか持っていないので、古典力学的には絶対に、-200Vの電圧を持つプレート②には達せず撥ね返るはずです。
しかし量子力学によれば、ある確率で電子はプレート②のポテンシャルの壁を破ります。それはプレート②の後ろに置かれた蛍光板が発光することで確認できます。蛍光板は電子が当たると、発光するものだからです。
突破不可能なはずのポテンシャルの壁に、電子がトンネルを穿ったようにみえるので、この現象はトンネル効果といわれます。トンネル効果は現実に存在します。それを応用した電子部品が江崎ダイオード(トンネル・ダイオード)です。現在、筑波大学の学長である江崎レオナ氏は、これでノーベル賞を取りました。
よって、もし量子力学が正しいのであれば、ハイゼンベルグのオリジナルな不確定性原理は、余りにも古典的描像に頼りすぎているといえます。ハイゼンベルグのやったことは、徹頭徹尾古典力学に基づいて電子の位置と運動量を測定するケースを考えたとしても、結局は量子力学的不確定性関係にたどり着くことを、わかりやすく示した例といえます。つまり我々は、どうやっても量子力学の制限からは逃れられないのだと。
またこの点がさらに厄介なのですが、「光子が衝撃力を持つという、観測に基づく量子効果をただ一点受け入れるだけで」、量子力学は決して古典力学と矛盾するものではないことを示した例でもあります。物理量の確率性とか、非局所的情報伝達とか、そのようなものが一目瞭然に古典力学と矛盾する現象を導けば、観測結果から自然はそういうものなんだと納得できるのですが、量子力学は日常的に何一つ顕著な効果を現しません。これの意味するところは、こうです。
「それを確かめる実証実験を思いつくことは、非常に難しい」
それを考え出したのが、ベルでした。
ところでオリジナルな不確定性原理が古典的描像に頼りすぎていることは、もちろんハイゼンベルグは百も承知でした。彼は、量子力学の基礎方程式を造った最初の一人です(もう一人はシュレーディンガーです)。
そして、不確定性原理という制限に由来する結果には、制限とは裏腹に、
という「センス・オブ・ワンダー(驚異の感覚)」が存在します。それが、ハイゼンベルグの控えめな論文に込められていた驚愕の事実です。
ところで、4.のEPR実験のところで、左電子が左1光年地点の上下方向磁場に飛び込んだ瞬間に、右電子に対して左右方向磁場のシュテルン・ゲルラハ実験を同時に行ったらどうなるだろう?、と思った人はいないでしょうか?。これを、EPR同時実験と呼んでおきます。
このような実験は、原理的にできるはずです。何故なら上下磁場発生装置と左右磁場発生装置を、電子発生装置から正確に左右1光年地点に配置すれば良いだけです。この際、不確定性関係(4)は関係ありません。磁場発生装置は巨視的物体なので、ワープすることなく不動の物体です。
結果はどうなるでしょう?。最も面白い結果は、左の上下磁場の影響50%,右の左右磁場の影響50%から、
というものでしょう。もしもそんな結果が得られたなら、これこそが「物理現象の非局所性の現れ」だと誰もが思ったことでしょう。
しかし現実はそうではないようです。私は、量子力学の正確な計算ができないので、こっから先は予想です。
さっき言ったように、表面上量子力学は古典力学と何一つ矛盾しません。EPR同時実験で、左電子に対して上下磁場を、右電子に対して左右磁場を同時に試しても、
それぞれ50%の確率で、それぞれ無関係に振れる.
だけだと思えます。理由は2つあります。
まず第一は、同時EPR室内実験は、誰かがもう試したと思えるからです。10年くらい前だったと思いますが、発射されてから数10cmしか進んでいないレーザー光の光跡写真が、話題になっていました。現在の測定技術は、それくらい進んでいます。さっきのEPR実験は、光の高速度を考えて1光年の距離を使いましたが、現在の測定技術をもってすれば、1光年を少なくとも1 kmくらいにまで短縮できるはずです。実際Cern(欧州連合加速器研究所)のシンクロトロンの輪ッかは、数kmの直径じゃないですか。実際に数kmの実験装置を造ることさえ、現在では可能です。誰かがやったにも関らず、(5)になったという話をとんと聞かないのは、やはり(5)が成り立たないからだと思えます。
もうひとつの理由は、(6)のようになると「ボーアの裁定」にはっきり書いてあるからです。「ボーアの裁定」には、こう書かれています。
「観測されたときに初めて、物理的実在と呼ばれるものが出現する」
と。
つまり左電子と右電子に対して、EPR同時実験を行った瞬間に、左電子と右電子はそれぞれ別の物理的実在に移行するからです。それは、
さらに、
からです。「ボーアの裁定」を正直に読めば、(6)のようなことが予想できます(あくまで予想ですが)。
これがその重みです。EPR同時実験や、量子力学で訳がわからなくなりそうな事態に出会った時に、誰も彼もが「ボーアの裁定」を頼りにしたのは、言われなきことではないと思います。ボーアは、アインシュタインに代表される日常的常識と量子力学のギャップを、ありとあらゆる場面で解決できるように、量子力学の認識論である「裁定」を考え出しました。それはとても簡潔なものです。
「簡潔」というのは相対評価です。実際のところ「ボーアの裁定」は長い長い文章です。しかし、それが扱った問題の大きさを考えると、「簡潔」という言葉がふさわしいと思えます。
ところでEPR同時実験で、左右電子の関連が失われてしまった場合、物理現象の非局所性は、どこにいったのでしょう?。心配(?)いりません。そこには排他的な観測を左右で同時に行った瞬間、関連が瞬時に失われたという非局所性があります。しかもこれは「ボーアの裁定」が言ったとおりの事実です。
ですがその場合は、スピンが保存量であるという前提はどうなったのでしょう?。保存量が保存できなくなることは、物理学では絶対の不可侵です。例えばエネルギー保存則が破れれば、永久機関も可能になります。
心配無用(?)です。もしも古典的言い方をするなら左右電子が無関係になった瞬間に、もともと「上下にスピン軸を持つ電子と左右にスピン軸を持つ電子の組を、電子発生装置が生成した」状態に移行したことになります。観測の影響から、生成時からもともとスピン量が保存してない状態へ、系が移行したので、それはそれで良いのです。このことは、古典的には絶対と考えられていた保存則さえ、量子力学では破れる可能性があることを意味します。もちろん完全に自由に破れる訳ではありません。今の場合であれば、スピン方向は保存しなくとも、スピン量のスカラー、つまり電子発生装置の仕事量は保存するという制限がつきます。このように量子力学は、周到なルールに従って表面上古典力学と何一つ矛盾しません。それは非常に厄介で、わかりにくい原因にもなります。
しかしなお、「そんなことがあるものか!」という意見は当然あると思います。ですがそれは「スピン方向は電子の生成時に決まっている」という古典的考えに縛られています。
じっさい電子発生装置自身すら、どちら方向の電子を生成したかはわかりません。それを確かめようとすると、シュテルン・ゲルラハ実験装置つき電子発生装置となります。電子が生成された瞬間に、シュテルン・ゲルラハ実験を行います。しかしそれが、電子のスピン軸の方向を決めます。
何故なら、
「観測されたときに初めて、物理的実在になる」
からです。このように「ボーアの裁定」には、見事に出口がありません。これがボーアの、アインシュタインにはなかった素晴らしさです。
はっきり言って、私は宇宙戦艦ヤマト世代です。イスカンダルのスターシアが、妹のサーシアを地球に送って、波動エンジンの設計図を地球に伝えたなどと見てしまった瞬間に、「シュレーディンガーの波動方程式か?」などと思ってしまった口です。松本零士が波動方程式をどれほど知ってるかは、まさに知りませんが、シュレーディンガーの波動方程式もハイゼンベルグの行列力学も、結局は不確定性原理を導き、粒子がワープする可能性を導きます。
何を言いたいかというと、欧米の物理研究者の中には、SFから物理の世界に入ったという人たちが結構いるらしいのです。これを言った人はアーサー・C・クラーク(映画2001年宇宙の旅,2010年宇宙の旅の原作者)で、彼は世界的に著名なSF作家であるだけでなく、現在の衛星放送の基礎理論を創った人でもあります。
彼は言います。1980年頃にインドで、衛星テレビ放送を試験的に始めたときに、その辺の子供たちが衛星放送センターのテレビを穴のあくほど終日見ていたと。その中には、その日暮らしの浮浪児までもいた。
にも関らず、その全員に、
ときいたら、
と応えたそうです。
最近、理系や工学系は色々言われていますが、こういう話を聞くと、理系も工学系もそんなに捨てたものではないのかなぁと思えます。というわけで量子力学は、粒子がワープする可能性を導くのですから、こんなに面白い話はないと思います。

NO.1516
2005.2.6. 小学名探偵 経路の個数
(2)3×3×3の立方体格子を考えます。つまり、(0,0,0)から(2,2,2)まで27個の
格子点があり、
各格子点は単位立方体の辺でつながっています(たとえば、(0,0,0)は(1,0,0)、
(0,1,0)、(0,0,1)に辺でつながっています)。
格子点(0,0,0)から対角の格子点(2,2,2)に至る経路として、各格子点を訪れる回数が
1以下(一度も訪れない格子点があっても
よい)である経路を考えます。このような経路はいくつありますか。

NO.1517
2005.2.13. 水の流れ 規則性の発見
「ある2以上の整数についての操作で、
では、次のように操作を変えて考えます。
(1)その整数が偶数なら2で割る。
(2)その整数が奇数なら3倍して1を加えて2で割る
を繰り返して行うと、必ず4→2→1に達する」 という問題です。
「ある与えられた2以上の整数から始めて、次の操作を行う。
ここで、問題です。一般に2以上の整数anが上の操作で
(1)その整数が偶数なら2で割る。
(2)その整数が奇数なら1を加える。
(3)その整数が1になるまで、(1)、(2)を繰り返す。
例:13→14→7→8→4→2→1
an→an-1→・・・→a2→a1→1
となったとき、整数anは「操作数」nを持つという。
例1:「操作数」3の整数 8→4→2→1 、 3→4→2→1
例2:「操作数」6の整数 13→14→7→8→4→2→1

NO.1518
2005.2.16. 夜ふかしのつらいおじさん 規則性の発見(2)
f(4)=3 {6、7、16}
f(5)=5 {5、12、14、15、32}
f(6)=8 {10、11、13、24、28、30、31、64}

NO.1519
2005.2.18. 佐野允信 規則性の発見(3)
a2=4のとき、a3=8,3
よって、f(3)=2
a3=8のとき、a4=16,7
a3=3のとき、a4=6
よって、f(4)=3
a4=16のとき、a5=32,15
a4=7のとき、a5=14
a4=6のとき、a5=12,5
よって、f(5)=5
a5=32のとき、a6=64,31
a5=15のとき、a6=30
a5=14のとき、a6=28,13
a5=12のとき、a6=24,11
a5=5のとき、a6=10
よって、f(6)=8
n=1のとき、
f(3)=2、f(2)=1、f(1)=1より、
f(n+2)=f(n+1)+f(n) ・・・(1)
が成り立つ。
n≧2のとき、「操作数」nの整数のうち、偶数の個数をg(n)、奇数の個数をh(n)とすると、
f(n)=g(n)+h(n) ・・・(2)
が成り立つ。a1=2より、an=2m(m≧2)のとき、
an+1=4m,2m-1
であり、an=2k+1(k≧1)のとき、
an+1=2(2k+1)
が成り立つ。従って、
g(n+1)=g(n)+h(n)=f(n) (∵(2)より) ・・・(3)
が成り立つ。さらに、
f(n+1)=2g(n)+h(n)=g(n)+f(n) (∵(2)より) ・・・(4)
が成り立つ。(4)より、
f(n+2)=g(n+1)+f(n+1)=f(n+1)+f(n) (∵(3)より) ・・・(5)
が成り立つ。以上より、
f(n+2)=f(n+1)+f(n) (n≧1)
が成り立つ。

 E-mail
E-mail
 戻る
戻る