| NO.1520 | 2005.3.6. | 水の流れ | １位のチーム数の期待値 |
京都大学の入試問題の過去問です。興味があったので出題します。
| NO.1521 | 2005.3.13. | DDT | 量子力学が思ったほど奇妙でないわけ(2) |
先日NO.1491で、相当にかっとんだ事を書いてしまいましたので、お詫びに以下の本を紹介したいと思います。この本の出自だけは確かと思えますので、お詫びになってればと願うのですが・・・。
種本は「量子力学の奇妙なところが思ったほど奇妙でないわけ，デヴィッド・リンドリー，青土社，1997年」です。
１．前回までのまとめ
シュテルン・ゲルラハ実験は、互いに逆向きのスピン軸を持つように生成された電子対について、次の実験事実をつきつけるものでした。この実験事実は量子力学で予想できるものです。
1) スピン軸が上下方向か左右方向かは、観測のやり方によって決まる。どちらの電子が例えば上向きになるかは、50％の確率である。それとスピン軸方向が観測のやり方によって決まることを考え合わせると、スピン軸方向は電子対の生成時に決まっていないことになるので、理論は常に確率的予想しかできず、実験も常に確率的結果しか出せない。
2) 従って、本質的に確率的なスピン量という物質の性質の存在は、逆に本質的に物質が、確率的存在であることを示す一例である。
3) そして2個の電子が何光年離れていようと、一方が上方向スピンなら他方は下方向スピンであり、一方が左方向なら他方は右方向スピンである。しかも上下か左右かは観測のやり方によって決まる。よって、それは物理現象の非局所性を意味する。
4) 何故なら、スピン軸が上下または左右方向にあるのかどうかを確認する確認実験の影響が、数光年離れた電子間で瞬時に伝わると考えなければ、3)は説明できないから。
5) よって物質は（物理的実在は）、原理的に観測者と独立でもなければ、その諸性質を無限に正確に測定できるものでもない。そして物理現象の効果が、瞬間的にどこまでも伝播する非局所性を持つ場合がある。
これがニールス・ボーアの立論です。アルバート・アインシュタインはこれに対して、逆の立論を行いました。
1) 物質は（物理的実在は）、原理的に観測者と独立であり、その諸性質は原理的に無限に正確に測定できるはずだ。そして物理現象の効果は非局所性を持たない。それが経験事実である。
2) 従ってスピン軸方向が数光年離れた電子間で、観測のやり方によって瞬時に決まるのであれば、そこには実験の影響を瞬時に伝えるように見える、まだ知られていないまっとうな物理的情報伝達機構があるに違いない（非局所性の解決）。
3) そのようなものがあるとすれば、スピン軸方向は常に確定したままなので、物質は（物理的実在は）本質的に決定論的に行動し、物質が確率的にしか存在し得ないようにみえるのは、見かけ上のことである。その諸性質は原理的には無限に正確に測定できる（確率性の解決）。
4) よって量子力学はそのような物理機構を記述できないという意味において、不完全である。
（日常性の回復）
2人の立論の方向が正反対なのは、注目に値すると思えます。そして2人の大御所の立論に判定を下すには、なお50年の歳月が必要でした。
しかし2人の大御所の立論は、2個の電子（複数個の物体）に関するものです。1個の物体（1個の電子）に対して、両者の言い分がどうなるかを見ておくと、事態ははっきりします。ハイゼンベルグの不確定性原理の帰結を思い出してください。それは、1個の電子の位置と速度には、回避しえない不確定性がつきまとうというものでした。そのためにトンネル効果が生まれ、漫画ちっくにいうと電子が現実にワープする可能性さえあり、実際にそれは観測されています（トンネル効果）。そしてそれは、位置と運動量の本質的な確率性と、位置の非局所性を導くものでした（トンネル効果により、電子は現実にワープする）。
例えばトンネル効果に対して、ボーアならこういうと思います。
「自然は観測の影響を受ける存在なのだ」
「古典論との対比で、物質が確率的に存在することを、量子状態にあるという」
一方アインシュタインにとって、電子はあくまで量子ではなく粒子です。その粒子がワープするからには、粒子のワープを許すような、物理的にまっとうな、物質転送機構が時空間に備わっていなければなりません。1個の粒子である電子は、その物質転送機構に載って動くだけで、電子自体はどこまでいっても確定した粒子という古典力学的存在です。その位置と速度は常に同時に確定したままで、それらが不確定に見えるのは物質転送機構のトリックだということになります。
ベルはこの点に気づきました。アインシュタインの観点に立てば、いかに粒子が量子的に振舞おうと、それは見かけ上のことなので、完全にランダムな結果を導く実験を多数行ったならば、そのランダムな実験全体の統計的性質は、普通の古典粒子に対する、普通のランダム実験の統計結果となんら変わらないはずです。
何故なら、電子が物質転送機構に載って動こうと動くまいと、その電子の位置と速度が常に同時に確定したままであることは、不変だからです。これは観測の影響とは無関係です。
一方ボーアのように、物質が常に量子状態にあると考えるならば、存在自体が確率的なので、そこには量子力学に固有な統計的性質が現れる可能性があります。そしてそれは観測に影響されるかも知れません。この違いは実証実験に持ち込めます。完全にランダムな結果を導く実験を、多数行えば良いだけだからです。
２．ベルの定理とアスペの実験
最初に言いますが、ベルとは電話を発明したグラハム・ベルではありません（間違う人もいないと思いますが、念のため）。1964年にジョン・ベルは、ベルの不等式の名で知られる論文を発表します。EPR実験からじつに30年後のことです。その間ボーアとアインシュタインは、公開討論の場でさんざん議論を闘わし、個人的にも書簡を取り交わし、書簡は公開されました。ですが、その全ては思考実験です。
思考実験とは、原理的には可能であるが、現実的にはとても不可能な実験をさします。たとえ現実的にはとても実行不可能であっても、そのような議論は、問題の所在とか、問題の本質とか、問題の再抽象化や論点の明確化をもたらします。
思考実験の価値は、理想状態における物理実験の帰結を明確にするので、論点の明確化に非常に役に立ちます。この発想法も最初に意識して提唱したのはアインシュタインですが、言ってしまえば、30年以上の机上の空論が闘わされた後に、初めてジョン・ベルが、ボーア−アインシュタイン論争に決着をつける実証実験を思いつきました。
これは思考実験の効果だとも言えますし、ジョン・ベルの才能だとも言えます。だって状況はみな同じだったのに、ベルだけが「ベルの不等式」を思いついたのですから。でもアインシュタインが思考実験を提唱しなかったら、「ベルの不等式」を思いついた「ジョン・ベル」が現れたかどうかは、わからないと思います。
ベルは、次のような実験を思い立ちます。今までのシュテルン・ゲルラハ実験では、上下方向と左右方向という直交方向の実験しか考えていませんでした。しかし例えば斜め45°とか、もっといえば1°刻みに磁場の方向をずらしてシュテルン・ゲルラハ実験を繰り返したら、どうなるでしょう？。「種本」には、こう書かれています。
上下磁場をくぐりぬけた電子対について、斜め45°方向の磁場をかけたら、どうなるだろう？。
斜め45°方向が、ここでは1時30分と7時30分の方向だとします。もしくは上下を南北，左右を東西として、北東−南西の方角です。「種本」では上下磁場をくぐりぬけた電子対の挙動は、北東にどちらかの電子が曲がる確率85％，南西に他方の電子が曲がる確率15％と書かれています。実際これは、量子力学的には、スピン軸ベクトルを北方向（y方向）と東方向（x方向）に、単純に射影をとって分解しただけの話です。
ですが、だまされてはいけません！。「種本」では、ものすごくあっさり書かれてあるので見落としがちなのですが、アインシュタインの立場を信じる限り、このようなことは絶対にあり得ないはずです。
たとえ無限に離れた距離間で相関を持とうとも、あくまでそれらの粒子が古典的存在であるならば、完全にランダムにセットされた磁石の影響は、その設定角度に対して一様でなければならないはずです。しかし一回でも上下や左右磁場をくぐりぬけた電子対は、その挙動に癖を持ちます。それが観測の影響を受けた量子状態です。それが「種本」が暗に語っていたと思われる等方性の破れ、または完全なランダムさの破れです。量子力学（種本）によれば、
「北東に一方の電子が曲がる確率85％」
「南西に他方の電子が曲がる確率15％」 (1)
です。一方アインシュタインの立場で考えれば、
「北東に一方の電子が曲がる確率50％」
「南西に他方の電子が曲がる確率50％」 (2)
になると思えます。ただし私は、正確な量子力学の計算ができないので、(1)と(2)の違いは、一種の概念図にあたるものだと考えて頂くのが安全です。ですが定性的には、(1)と(2)の違いは、ワープ機構のあるなしに関らず、電子が古典的粒子であるか、それとも量子的存在であるかで決定されるように思えます。
上記挙動の違いを確かめる実験の結果は、1982年にアスペによって報告されました。ベルの論文からさらに18年。量子状態に関する多数の精密実験を行うには、測定技術の進歩を待ちつつ、約20年の歳月を要したということです。EPRからは実に50年でした。
ベルの定理とは、電子が（物質が）古典的な粒子的存在と仮定して、それに対する完全ランダム実験の結果が持たなければならない、ある統計的不変量を導く代数的手続きです。ベルの不等式ともいいます。
３．結果は？
アスペの実験は、ベルの定理の反例になりました。たとえアインシュタインが想定したワープ機構が時空間に現実に備わっていたとしても、そこを通り抜ける電子は（物質は）、アインシュタインが望んだような単純で常識的な古典的存在ではなかった、ということです。
アインシュタインは、観測の確率性は見かけ上のことであり、本来確定した観測量を持てるはずの物質が、ワープ機構の擬似非局所性のために、そう見えるだけだという可能性を提起しました。EPR実験における、その辺りの立論は実に見事です。
しかし、アスペの実験結果は、それを否定します。一回でも上下や左右磁場をくぐりぬけた電子対は、その挙動に癖を持っていて、観測の影響が電子の存在の仕方を変えてしまったと考えざる得ません。ここから導かれる結論はこうです。
アインシュタインは、「実在の確率性」と「物理現象の非局所性」は不可分のものと思っていました。そして物理現象を決定論的に記述できない量子力学は、不完全だと判断したのです。
実際アインシュタインの立場では、「物理現象の非局所性」を納得できる形で解決できる「隠れたパラメータ理論（いわば時空間に自然に備わっているワープ機構）」が存在すれば、「実在の確率性」は同時に解消できます。
ところが、たとえアインシュタインが暗に提唱したワープ機構による「物理現象の非局所性」があったにしても、それとは独立に、物質は常に量子状態にある「確率的存在」であることを、アスペの実験は実証したことになります。
４．シュレーディンガー方程式の起源
困った事態になりました。(3)を認めると、アインシュタインがめざした実在の確率性の解決は望めません。これは、観測問題の本質に直面せざる得ないことを意味します。これがどれほど困った事態であるかは、後ほど述べますが、観測問題の本質を理解するには、まずシュレーディンガー方程式を定性的にでも理解する必要があります（と、あくまで思うだけですが）。
シュレーディンガー方程式の起源にも、ニールス・ボーアは関っています。ボーアは1913年、古典論における電子縮退問題の解決と、電子が発生するスペクトル光の不連続性を説明するために、プランクの黒体輻射理論を参考にして、原子に関するボーアの量子条件を発表します。それは、電子の運動量をp，電子の軌道半径をaとして、
というものでした。(4)を受け入れると少なくとも水素原子に関しては、電子縮退問題と発生スペクトルの不連続性（ライマン・パルマー系列）が見事に説明されます。ここでhはプランク定数で、nは1以上の整数です。この段階の量子力学を前期量子論といいます。
大成功した関係(4)に、ド・ブロイは、アインシュタインの光量子理論を結びつけることを思いつきます。なぜ結びつける気になったのかは、すぐ後に述べますが、とにかくそれをやれば、光量子理論では、
なる関係があるので、これを(4)に代入すると、
となります。ここでλは波長であり、光量子理論(5)におけるλは、もちろん光の波長です。またpは光の運動量です。それらを、電子の運動量pと電子の波長λに読みかえると式(6)となります。しかし電子の波長とは何でしょう？。式(6)を正直に読んでみます。
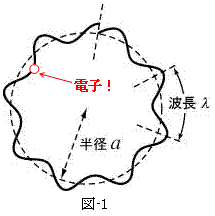2πaとは電子軌道の周長です。そこをきっちり整数倍の波長λでもって電子が周回しているとは、図-1のように、電子は半径aの軌道上を、ある定常波となって周回していることになります。ド・ブロイはこれを物質波と呼びました。ド・ブロイは「電子はある波動軌道に載って運動する」と考えたのです。
ではド・ブロイは、何故そのようなことを考えたのでしょう？。それはアインシュタインの光量子理論の成功にあります。古典的光の理論であるマックスウェル理論によれば、光は完璧な横波で、直接的な圧力を反射物体には及ぼしません。光が物体に影響を及ぼすのは、エネルギー交換とかのあくまで間接的な影響で、光が直接物体をキックするとかの直接的影響は、マックスウェル理論では考えられないものでした。それを否定したのが、アインシュタインは光量子理論です。光を反射することによって、鏡が圧力を受けるというのが、光量子理論の結論です。マックスウェル理論での光の扱いと、ド・ブロイのイメージを図-2に示します。
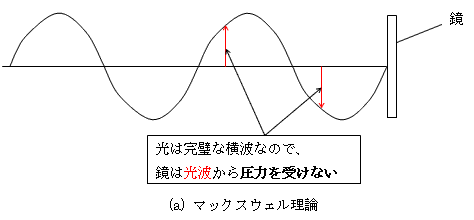
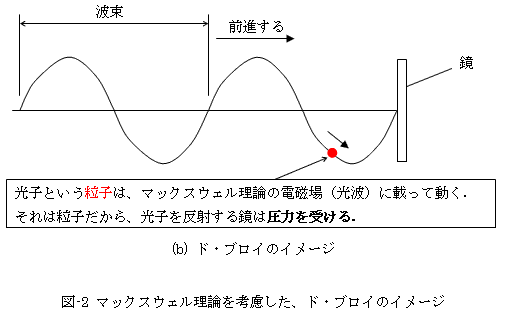
しかし光の運動量とは何でしょう？。マックスウェル理論によれば、光は波です。従って波束全体の前進を考えれば、波束移動のエネルギー伝播に伴う運動量移動を考えることはできますが、それはあくまでも上下方向運動に限られた運動エネルギーの伝播であって（図-2-(a)）、それが直接、光を反射する鏡をキックすることにはなりません。アインシュタインの光量子理論の運動量は、光が直接鏡をキックする、その強さを表す運動量です。そうであるためには、光は縦波成分も持っていなければなりませんが、それはマックスウェル理論から否定されます。この二つの矛盾する現象を直感的に理解するために、ド・ブロイは、図-2-(b)のような描像を提唱しました。光量子理論が暴いた、光は光子という粒であるという事実を、より明確に提唱したわけです。
しかし完璧な波動そのものと思われていた光波が、じつは粒子だったのです。しかもそれは、図-2-(b)のような非常に古典的な描像で納得できます。とすれば、完璧な粒子そのものと思われていた電子が、じつは波動であったということもあり得ます。そう思ったド・ブロイは、光量子理論における関係式(5)を、ボーアの量子条件(4)に試してみます。結果は大当たりでした。それが(6)です。電子は、その周回軌道上の定常波に載って運動する粒子だ、という結論になります。
シュレーディンガー方程式は、ド・ブロイの物質波を、非相対論的なあらゆる場面で計算できるように拡張したものです。シュレーディンガー方程式の考えを光に適用すると、電磁場の場の量子化という面倒な手続きを経た後にですが、光波を表すマックスウェル方程式が現れます。シュレーディンガー方程式は、完璧な粒子と思われていた電子の物質波を記述するように、完璧な波と思われていた光の物質波をも、矛盾することなく記述できる能力を秘めています。
５．シュレーディンガー方程式の解釈
その後、シュレーディンガー方程式は、非相対論的な局面におけるあらゆる量子実験（実現可能なあらゆる量子実験）を説明していき、量子力学の最初の基礎方程式となりました。現在でも基礎方程式であることに変わりなく、古典力学におけるニュートンの運動方程式と同等な位置づけです。
シュレーディンガー方程式が発表された当初、最初アインシュタインは積極的にそれを支持します。シュレーディンガー方程式（別名、波動方程式）の解である波動関数こそが、「実在の確率性」と「物理現象の非局所性」を解消すべき物理機構を表す数学的表現だと思ったからです。数学的表現が得られたからには、あとはそれを物理的に解釈すればいいわけです。ちなみに波動関数は、ボームの「隠れたパラメータ理論」の原型にもなっています。
シュレーディンガーの波動関数を物質波と考えた場合、しかしそこには一つの難点がありました。波動関数がド・ブロイの考えたような物質波であるならば、それは波動軌道です。それがいくら波打っていたところで所詮軌道は軌道であり、1本のラインにすぎません。その自由度は3（3次元）でなければならないはずです。ところがシュレーディンガーの波動関数は、波動場でした。場であるからには、原理的には全空間に（宇宙の果てにまで）拡がっています。つまりその自由度は、無限大となります。場とは全空間の全ての点で同時に定義される関数、だからです。
１個の電子ではなく、量子状態にある多数の電子集団を考察したボルンは、気体分子の統計的振る舞いを記述する古典統計力学を参考に、「シュレーディンガーの波動関数の二乗値が、1個の電子がある位置で観測される確率を表す」という結論を導きます。これを、ボルンの確率解釈といいます。黒体輻射に関するプランクの量子仮説の場合もそうですが、古典統計力学は、量子条件の発見やその解釈のための雛形となっています。
ボルンの確率解釈は、その後のボーアに代表される、量子力学のコペンハーゲン解釈の原型になっていきます。波動関数が波動軌道でなく単なる確率場であるならば、自由度が無限大になってもかまいません。というか場の定義からして自由度無限大は当たり前です。しかし波動関数は、単なる確率場にとどまれないのです。ボルンの確率解釈を、トンネル効果に対して適用してみます。
ハイゼンベルグの不確定性原理が示したように、1個の粒子の位置には、ある一定の不確定さがつきまといます。つまり、これこれの位置に粒子が観測される確率は、これくらいだというわけです。この確率は極端な場合を除いて全くの任意ではありません。例えばNo.1515のトンネル効果検証用真空管の例でいうと、電子を跳ね返すプレートAを突き抜けて、その後ろの蛍光版に電子が達する確率は、もちろん電子を加速するプレート@の電圧が上がれば上がる程、大きくなります。原理的に電子が見出される確率分布は、全空間に拡がっているのですが、その確率分布には濃いところや薄いところがあり、また時間的にも変化します。この空間的な確率場の濃淡の時間的変動は、波のように伝播し、それを記述するのがシュレーディンガーの波動方程式です。そして単なる確率場であるはずの波動関数からは、再び不確定性原理が得られます。
逆にプレート@が300Vの電圧を持っていて、古典力学的には絶対にプレートAを突破するだけのエネルギーを電子が持っている場合でさえも、電子はプレートAで跳ね返って、その手前で発見される確率も0ではありません。それらは全てシュレーディンガー方程式で、確率的に予測できます。
しかし「粒子がある位置である確率で観測される」とは、物理的にはいったいどういう事態をさすのでしょう？。電子が真空管のカソードで発生して蛍光板に達したのは確かと思えます。でもシュレーディンガー方程式は、電子がどのような経路をたどって蛍光板に達したのか教えてくれません。
波動関数を確率場だとするボルンの解釈をそのまま受け入れれば、「蛍光板にぶつかるまで電子はあまねく全空間に同時に存在する確率的何か」です。「全空間に同時に存在する電子」が蛍光板にぶつかった瞬間に、どうやって蛍光板の1点に収束したかわかりませんし、そもそも「全空間に同時に存在する電子」がどうやって蛍光板にぶつかれるのかさえ、見当もつきません。でもそこが知りたいところです。
これを波動関数の波束の収縮といいます。みんな確率波の収縮とは何か？を知りたいのです。この頃から、ド・ブロイもアインシュタインも、シュレーディンガー方程式に対して「アレレッ？･･･」と思うようになってきます。何故ならボルンの確率解釈が正しいならば、「実在の確率性」と「物理現象の非局所性」を解消する物理機構の可能性を提示したかのように見えた波動関数が、じつは「実在の確率性」と「物理現象の非局所性」そのものを表す何かに化けてしまうからです。
６．波束の収縮を実験にかけてみる
確率波の収縮とは何か？とは、結局どのような経緯で、そこに電子が発見されたかの機構を知りたいということです。量子力学における観測の成立機構を知りたいのです。これが観測問題の原型です。では、波束の収縮を実験にかけてみます。
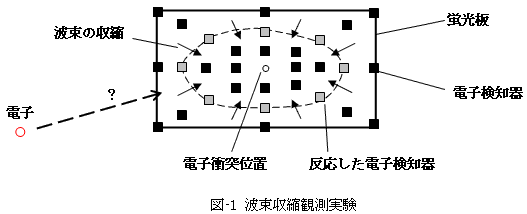
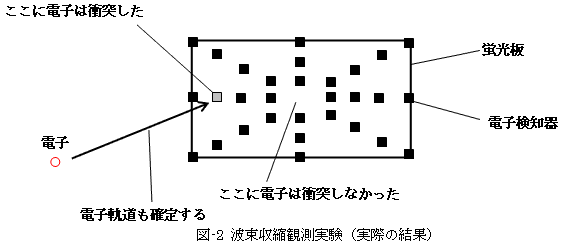
図-1のように、蛍光板の中心を狙って電子を打ち出します。もちろんさっき言ったように、電子軌道には不確定さがつきまとうので、ある確率でしか蛍光板の中心に電子は衝突しませんが、多数の電子を用いれば、いつかはまぐれ当たりするはずです。このとき蛍光板の中心には、電子の衝突を示す輝点が現れます。
もし波束収縮の観測がうまくいったならば、蛍光板の中心に輝点が現れる直前に、そのまわりに配置された電子検知器のどれかが反応し、反応した検知器を点線で結んでいけば、収縮する波束の形がわかるかもしれません。さらにもっとうまくいけば、検知器の反応時間の時系列を追うことによって、→ で表したような波束の収縮アニメーションさえ描けるかもしれません。
しかし実際には、図-1のようなことは起こりません。「検知器のどれかが反応した」ということは、「そこに電子が衝突した」ことを意味します。実際に得られる状況は図-2です。つまり波束の収縮が物理的機構として存在すると仮定しても、その波束を測定する観測そのものが、その観測器への波束の収縮を招いてしまいます。それだけでなく、図-1では「？」だった電子の軌道さえ、図-2では確定します。観測が成立した瞬間に、電子は確率的存在であることを止め、確定した粒子としての実在性を獲得するからです。これらは全て観測した後 でわかることであって、観測していない間は、それらに関して語ることは無意味です。何故なら言ってしまえば、観測自体が物理的実在の姿を決定するからです。要するに「ボーアの裁定」です。
「物理的実在は、観測者と独立ではない。
観測されたときに初めて、物理的実在と呼ばれるものが出現する」
からです。「ボーアの裁定」には出口がないのです。
少し考えればわかりますが、デジタル的に電子検知器を配置した蛍光板の波束測定のアナログヴァージョンとは、蛍光板という素材そのものです。蛍光板への電子衝突などは、世界中のいつでもどこでも常に、テレビのブラウン管の中で起こっています。ブラウン管とは、蛍光板への電子衝突を利用したディスプレイ装置のことです。にもかかわらず、電子衝突を表す蛍光輝点の周囲に、波束の存在を示す蛍光輝線が現れたということは、古今東西一度たりとも観測されていません。テレビをつけてみればわかります。
観測問題の解決は不可能なようにみえてしまいます。ベル−アスペの実験は、「物理現象の非局所性」の物理的に正当な解決に基づく「実在の確率性」の解消という、アインシュタインの望みにとどめを刺しました。自然は「非局所的存在」であり「確率性存在」でもあったのです。すくなくとも素人である我々とっては、この結論は受け入れ難いものです。でも受け入れ難かったのは、何も我々だけではありませんでした。当時まだベル−アスペの実験は知られていませんでしたが、シュレーディンガー方程式をつくり出したシュレーディンガー当の本人が、自分が生み出したものに納得していませんでした。悩んだ末に彼は、今日「シュレーディンガーの猫」で知られる象徴的な例を思いつきます。
７．シュレーディンガーの猫
シュレーディンガーの猫実験とは、こんなお話です。
左右方向に電子が飛び出す上下方向のシュテルン・ゲルラハ実験を行います。行いますが、今回測定にかけるのは、右電子のみです。右電子が上下磁場に飛び込んで上に曲がるか、それとも逆かは50％の確率です。右電子が50％の確率で上に曲がった場合、そこには電子検知器が待ち構えています。電子検知器は電子を捉え、ある電気信号を出します。一方、完全防音の箱に閉じ込められた猫がいるとします。箱の中身はこれまた完璧に見えません。箱の内部には、猫を狙ったボーガンがセットされており、ボーガンのトリガーには先ほどの電子検知器がつながっていて、ボーガンのトリガーは電子検知器の電気信号を待っています。もし電子検知器が応答すれば、完全防音の箱に閉じ込められた猫は音もなく葬り去られます。また音もしないし中身も見えないので、観察者は箱の蓋を開けない限り、猫の生死はわかりません。
さて。逆向きのスピンを持つ電子対が一組生成され、左右にわかれてシュテルン・ゲルラハ実験が行われました。右電子は上向きスピンだったのでしょうか？、それとも下向きだったのでしょうか？。それは箱の蓋を開ければわかります。猫が死んでいれば上向きであり、運良く生きていれば下向きだったとわかります。ここまでは問題ありません。では、箱の蓋を開ける前の状態では、スピンはどちら向きでしょう？。これを、ボルンの確率解釈による電子の位置観測と比較してみて下さい。ことの重大さがわかります。
ボルンの確率解釈を信じる限り、電子は測定されるまでは（蛍光板に衝突するまでは）、あまねく全空間に同時に確率的に存在する状態でした。測定されるまでの電子は、全空間のあらゆる場所に同時に存在していたことになるのです。そして何故そうなるのかは皆目わからず、それを解決するかに見えたアインシュタインの儚い望みさえ、ベル−アスペの実験は否定しました。そのような状態は、シュレーディンガー方程式によって記述されます。そしてシュレーディンガー方程式は、シュテルン・ゲルラハ実験にももちろん適用可能です。
「シュレーディンガーの猫実験」での観測とは、箱の蓋を開けることです。ということは、箱の蓋を開けるまで、右電子のスピン状態は、同時に上向きでもあり下向きでもあった、ということになります。
電子は日常生活（巨視的系）には決して表に現れない極微の存在です。だから、それはそれで良いのかも知れません。「シュレーディンガーの猫」の価値は、そのような逃避を許さないところにあります。
今の場合、猫の生死は、直接電子のスピン方向に1対1に対応しています。ということは、箱の蓋を開けるまで、猫は同時に死んでもいるし生きてもいることになります。このようなことが、現実に起こらないのは確かです。しかし、量子力学の基礎方程式であるシュレーディンガー方程式と、ボルン−ボーアのコペンハーゲン確率解釈を信じれば、このような事態が結論されます。またその解決をめざしたアインシュタインのプログラムは、現状では挫折したままです。
埒が明かないので、ここは常識的に考えてみましょう。常識的に考えれば、電子検知器に右電子が捉えられた瞬間に観測は成立し、右電子のスピン方向は上向きで、猫が死ぬことは確定します。つまり常識的判断では、「シュレーディンガーの猫実験」での観測成立時は、電子検知器の反応時なのです。何故そう思うのでしょう？。
「シュレーディンガーの猫実験」や、その他膨大な数の粒子加速器内での実験結果などを、約100年間にわたって実際に見続けた物理学者達は、次のような判断を下しました。
「量子効果が顕著なミクロな系（電子）が、
量子効果がほとんど現れないマクロな系（蛍光板）と相互作用した時、
観測が成立する」 (1)
と。電子検知器は、単純な素粒子である電子に比べれば、膨大な質量と複雑さを持ちます。それが常識的判断の根拠です。ですが本当にそうでしょうか？。
電子検知器は、量子効果が顕著でミクロな電子という物体を捉えます。ということは、電子と実際に相互作用する部分は、恐ろしく精妙でミクロなはずです。全ての測定器には、起歪部とか起電部とか起振部とか言われる、恐ろしく精妙でミクロな部分があります。今の場合それは起電部であり、1個の電子が衝突するだけで反応するような、量子効果が顕著でミクロで精妙な部分でなければならないはです。そこから発信された電気信号に、量子力学的な不確定さが付きまとっていないと言えるでしょうか？。さらに電気信号で検知器と結ばれているボーガン・トリガーがあります。電気信号とは電子の流れです。電子とは、量子効果が顕著でミクロなものです。だとすれば、信号そのものの不確定さが、信号を運ぶ電気信号に伝わって、ボーガン・トリガーが起動するしないに、量子力学的不確定さが影響しないと言えるでしょうか？。ボーガン・トリガーの起動の有無は、猫の生死に直接対応します。結局猫の生死に、その不確定さが持ち越されます。観測はどこで成立したのでしょう？。
では百歩譲って、「箱の蓋を開けた時が観測成立時」だとします。これを認めるだけでも大変なことなります。蓋を開けるまで、猫は同時に死んでもいるし生きてもいることになるからです。たとえここまで譲歩したとしても、なお問題があります。
我々は蓋を開けたとして、猫が死んでいるか生きているかを、どうやって知るのでしょう？。猫が死んでいた（または生きていた）状態を知るためには、まず猫に反射した光を眼で見る必要があります。ところで光子とは量子効果が顕著でミクロな何かであり、しかも猫の生死に量子的な不確定さがあることを、たった今認めました。蓋を開けた瞬間が観測成立時ではなく、我々の眼に光子が捉えられた瞬間こそが、観測なのかもしれません。そうでないことは実証できないのです。確率波の波束収縮測定は、全て失敗するからです。
ところが我々の眼にも、立派な起電部があります。網膜と視神経です。網膜は、たった1個の光子（ではないと思いますが、ここは原理的な話です）にも反応するような、量子効果を受けやすい非常に精妙でミクロな機構です。視神経は電気信号を伝えますが、電気信号とは電子の流れであり電子とは量子効果が顕著な・・・。観測はどこで成立したのでしょう？。どこでミクロな系は、巨視的でマクロな物体と出会ったのでしょう？。
８．解決をめざした二つの極論
量子力学の観測問題が、どれほど異常な事態であるかを、わかって頂けたでしょうか？。この異常事態の常識的解決をめざしたアインシュタインのプログラムは、現在のところベル−アスペの実験結果により再起不能です。ここでは異常事態の解決をめざした、二つの極論を取り上げます。
一つは、「心理物理学」というものです。これはさっきの「視神経の電気信号とは電子の流れであり電子とは量子効果が顕著な・・・」の後をどこまでも肯定し、「途中経過はわからない」が、「猫の状態を我々が認識した瞬間に観測が成立する」としたものです。その時に確率波の収束が起こるのです。
そう考えても、実現象とは何の矛盾もありません。確率波の収束が実証できない以上、情報伝達の流れを詳細に追跡すれば、何故かはわからないが、我々が認識した瞬間が観測成立時なのかも知れません。実現象とは我々が認識したものだからです。まさに「我思う、故に我あり」みたいな話ですが、具体的に反証できません。
「心理物理学」は量子力学の認識論の枠内で、物理学者達により真面目に議論されました。そこでは第一の観測者が蓋を開けて猫の生死を知り（第一観測者にとって、情報が脳細胞に届く微小なタイムラグを除いては、確率波の収束は蓋を開けた瞬間だとして）、第一観測者が第二観測者にその情報を電話で知らせたなら、第二観測者にとっての確率波の収束は、電話をとった瞬間か？、とかいうことが大真面目に議論されました。これ以上は言いませんが、第二次世界大戦後のピカ一の物理学者といわれたファインマンが、この「心理物理学」に半分くらい傾いていた形跡があります。ファインマンは、その「自伝」で述べているように、ボルンの確率解釈に端を発するシュレーディンガーの確率波動場の概念が、実在論的にはどうしても理解できませんでした（アインシュタインと同じです）。そして彼は「心理物理学の態度で研究しても良いのだ」ということを示そうとします。ただしそのやり方は逆説的です。彼は、人間の認識作用とは独立な物理的実在の存在を信じていたと思います。
確率波の収束が実際に観測できない以上、我々が認識した瞬間に実現象が成立するとしても反証できません。 だとすれば、そうやって成立した観測結果が、古典論と矛盾しなければ良いのです。彼は「心理物理学」が正しいとしても、それによって古典力学が破綻しないことを望みました。悩んだ末に彼は、量子力学を古典論的に再解釈することを試みます。それは、経路積分法を生み出しました。
経路積分法とは次のようなものです。シュレーディンガーの確率波動場は、粒子の存在確率に対して濃いところや薄いところを、空間的に与えます。ファインマンは、その最も濃いところが古典的粒子軌道になるのではないかと考えました。その最も濃いところに粒子軌道を想定したとしても、しかし確率的に薄いところにも、量子的には古典的粒子軌道が存在します。だとすれば、全空間に対して可能な全ての粒子軌道を想定し、確率波動場の確率に従って、可能な全ての古典的粒子軌道の確率的期待値重み付け平均を計算したら、何が現れるだろうと彼は考えました（まっとうな考えですよね？）。
確率波動場の確率に従った可能な全ての粒子軌道の重み付け平均は、古典的粒子軌道に一致したのです。経路積分法は、その後ファインマン・ダイヤグラムを生み出し、結局それは繰り込み理論へとつながって、彼は朝永振一郎，シュウンガーと供にノーベル賞を受賞します。量子力学がわからないわからないと言いながら、まがりなりにもノーベル賞を取ってしまうあたりは、ファインマンのすごさです。現在では、超弦理論などの研究において、ファインマン・ダイヤグラムは必要不可欠な道具になっています。やっぱり古典的描象は非常にわかりやすいのです。経路積分法は、量子力学と古典力学を直接対応させる非常に有用な方法です。そしてそうしても良い原因は、確率波の収束が実際に実証できない以上、我々が認識した瞬間に実現象が成立するとしても良いからです。
第二の立場は、ヒュー・エヴァレットの超多時間理論です。ヒュー・エヴァレットは、アメリカのプリンストン大学にいた独創的な物理学者です。そういえば、アインシュタインもボームもファインマンもプリンストンにいました。どうやらプリンストンは、独創的な物理学者の宝庫のようです。
エヴァレットは、「シュレーディンガーの猫実験」を次のように考えます。
彼は、いつ観測が成立したかを問いません。ただ可能性として「生きた猫の状態」と「死んだ猫の状態」が量子的に同時に可能であるならば、どちらも現実として可能だと考えます。ボルンの確率解釈を信じる限り、どちらも同時に現実に起きるからです。でも実際には、どちらか一方です。
例えば「生きた猫」が観測された事実なら、「死んだ猫」状態は別の平行宇宙で存在すると彼は考えます。量子的には、どちらも50％の確率で同等な権利を持つ現実的存在だからです。彼は、観測の物理機構の説明を諦めて結論を出しますが、これも反証はできません。平行宇宙には原理的に行けないからです。
どうしてでしょう？。それは相対性理論により、過去には戻れないからです。量子効果により偶然に一方を選択させられた我々は、もう一方の宇宙にはいけません。
彼の理論に従えば、我々が「生きた猫」状態を、量子効果により偶然に選択させられた瞬間、全宇宙の歴史は二つに分裂します。分裂した全宇宙の歴史の一方には「生きた猫」がおり（我々の宇宙）、他方には「死んだ猫」がいます。観測を行う度に全宇宙の歴史が分裂するので、これを超多時間理論といいます。
歴史とは時間のことです。それが「観測を行う度に分裂する」ので、時間（歴史）の種類は超多様（超多時間）ということになります。別の宇宙に行くためには、過去に戻ってやり直すしかないのですが、それは相対性理論により禁じられています。
反証できない以上、超多時間理論は真実かもしれません。しかし超多時間理論は、観測問題を観測問題よりもっと良くわかっていない「時間の理論」に責任転嫁しています。この理論は魅力的ですが、もう少し地を這うような地道な議論が必要な気がします。ファインマンはその点、まさに地を這うような経路積分法を考え出し、それは非常に有用なものになりました。
今回はここでやめます。例によって、以下は周辺情報です。
９．心理物理学について
「心理物理学」の根っ子には、もちろん「ボーアの裁定」があります。「ボーアの裁定」をとことんまで突き詰めたらどうなるだろう？という本が、日本人の手によって書かれています。
「唯心論物理学の誕生，中込輝明，海鳴社，1998年」です。この本が物理学会の主流となり、学会をリードするということはきっとないと思いますが、読めば非常に面白い本です。中込輝明氏は、日本評論社から出ている「数理物理学方法論序説」の著者である保江邦夫先生の盟友でもありました。
10．EPR実験について
EPR室内実験は、やはり実行されていました。ベル−アスペの実験の追試という形で、10指に余る再実験が行われています。それらは全て、ベル−アスペの実験を支持します。それだけでなく、今ではEPR実験は全て、EPR効果実験と呼ばれています。いまや情報伝達の非局所性（EPR効果）は物理学会の常識になっています。EPR効果は、量子暗号や量子コンピューターの基礎理論にもつながります。試しに「量子コンピューター」をインターネットで検索したら、37000件もHitしました。その中には「量子テレポーション」なんてのもありました。まさに物質転送機構ですが、転送速度は光速以下です。
この量子暗号や量子コンピューターの可能性を世界で2番目に語ったのは、リチャード・ファインマンです。彼は1982年に、EPR効果を応用した量子暗号や量子コンピューターの可能性、そしてナノテクノロジーについて講演しています。シュレーディンガーの確率波動場の概念を、実在論的にはどうしても理解できなかったファインマンは、量子力学について徹底的に考え抜いたのです。ノーベル賞をもらった後、ファインマンは量子力学について余り語っていませんが、徹底的に考察したのでなければ1982年などという早い時期に、量子コンピューターの可能性について言及できるわけがありません。
ファインマンの考えに従った量子CPUのことを、現在ではファインマン･プロセッサーといいます。ちなみにファインマンとは、Windowsなどが走っている、現在のプログラム内蔵型コンピューターの原型を提唱した人でもあります。
というわけで、アインシュタイがEPR思考実験で反証しようとした事実は、多くの物理実験により実証されてしまった、というのが現在での状況です。
11．しかし観測問題は解決できる
しかし観測問題は、標準的量子力学と古典統計力学の発想だけでもって、物理的に正当に解決できる目途がたってきた、というのが「種本」の結論です。これは恐らく「種本」の白眉だと思えます。そこでのキーワードは、「コヒーレント」です。
「観測問題」「非局所性」「確率性」を比べてみると、「観測問題」が抜群に難しそうに思えます。それは、「非局所性」と「確率性」を解決した後でないと、解決できないように見えるからです。しかし現実は違います。この「観測問題」も、「非局所性」や「確率性」とは独立な問題でした。それを示しつつあるのが、「コヒーレント理論」です。
| NO.1522 | 2005.3.13. | Pogopogomanger | 鳩の巣の問題・その後 |
早速ですが、
鳩の巣の問題 問題２ に対する
解答投稿の中、その４、その５、その６に疑問を呈させて頂きます。
「 ３つのの解答いずれも証明し得ている命題は同一で、
『 100以下の自然数に属する異なる51個の自然数の任意の組み合わせAに関して、 ”Aの中の全ての51個の要素に関して、1以外の或る自然数kがそれら51個の共通因数 として存在する” という命題は常に偽である。』ということに留まり、これは題意の要求する
『 100以下の自然数に属する異なる51個の自然数の任意の組み合わせAに関して、 ”Aの中の任意の異なる2個の要素に関して、1以外の或る自然数kがそれら2個の共通 因数として存在する” という命題は常に偽である。』よりも弱い命題である。」
（蛇足その１：後者のkの値は2個の要素の選択に依存しており、A全体に対して共通
な値である事を要求されない。）
（蛇足その２：「前者が後者よりも弱い命題である。」をより言葉を費やして述べれ
ば、
「整数論的公理に基づく式変形や命題変形を行う事無く形式論理的に比較すれば、前
者は後者の必要条件であるが充分条件ではない。」）
（蛇足その３：任意のAに関して否定されている”〜”内の命題の包含関係は当然逆
で、前者のそれは後者のそれの充分条件であるが必要条件ではない。）
以上が僕の認識ですが、いかがでしょうか。
| NO.1523 | 2005.3.13. | 佐野允信 | １位のチーム数の期待値(2) |
４チームのチーム名をそれぞれＡ，Ｂ，Ｃ，Ｄとする。ＡとＢが対戦することを
Ａ − Ｂ
と表すことにし、ＡがＢに勝つとき、
○Ａ − Ｂ×
のように、○と×をつける。リーグ戦なので全部で６試合あり、それらは次の通りである。
Ａ − Ｂ
Ａ − Ｃ
Ａ − Ｄ
Ｂ − Ｃ
Ｂ − Ｄ
Ｃ − Ｄ
勝ち数のパターンは次の４通りである。
(1) （３勝、２勝、１勝、０勝）
(2) （３勝、１勝、１勝、１勝）
(3) （２勝、２勝、１勝、１勝）
(4) （２勝、２勝、２勝、０勝）
(1) （３勝、２勝、１勝、０勝）の場合
例えば、Ａが３勝、Ｂが２勝、Ｃが１勝、Ｄが０勝とすると、下図のようになる。
○Ａ − Ｂ×
○Ａ − Ｃ×
○Ａ − Ｄ×
○Ｂ − Ｃ×
○Ｂ − Ｄ×
○Ｃ − Ｄ×
従って、Ａ，Ｂ，Ｃ，Ｄの並べ替えを考えると、この場合、
１×４！＝２４通り
存在する。
(2) （３勝、１勝、１勝、１勝）の場合
例えば、Ａが３勝、Ｂが１勝、Ｃが１勝、Ｄが１勝とすると、下図のようになる。
○Ａ − Ｂ× ○Ａ − Ｂ×
○Ａ − Ｃ× ○Ａ − Ｃ×
○Ａ − Ｄ× ○Ａ − Ｄ×
○Ｂ − Ｃ× ×Ｂ − Ｃ○
×Ｂ − Ｄ○ ○Ｂ − Ｄ×
○Ｃ − Ｄ× ×Ｃ − Ｄ○
従って、Ａ，Ｂ，Ｃ，Ｄの並べ替えを考えると、この場合、
２×４＝８通り
存在する。
(3) （２勝、２勝、１勝、１勝）の場合
例えば、Ａが２勝、Ｂが２勝、Ｃが１勝、Ｄが１勝とすると、下図のようになる。
○Ａ − Ｂ× ○Ａ − Ｂ×
×Ａ − Ｃ○ ○Ａ − Ｃ×
○Ａ − Ｄ× ×Ａ − Ｄ○
○Ｂ − Ｃ× ○Ｂ − Ｃ×
○Ｂ − Ｄ× ○Ｂ − Ｄ×
×Ｃ − Ｄ○ ○Ｃ − Ｄ×
×Ａ − Ｂ○ ×Ａ − Ｂ○
○Ａ − Ｃ× ○Ａ − Ｃ×
○Ａ − Ｄ× ○Ａ − Ｄ×
×Ｂ − Ｃ○ ○Ｂ − Ｃ×
○Ｂ − Ｄ× ×Ｂ − Ｄ○
×Ｃ − Ｄ○ ○Ｃ − Ｄ×
従って、Ａ，Ｂ，Ｃ，Ｄの並べ替えを考えると、この場合、
４×６＝２４通り
存在する。
(4) （２勝、２勝、２勝、０勝）
例えば、Ａが２勝、Ｂが２勝、Ｃが２勝、Ｄが０勝とすると、下図のようになる。
○Ａ − Ｂ× ×Ａ − Ｂ○
×Ａ − Ｃ○ ○Ａ − Ｃ×
○Ａ − Ｄ× ○Ａ − Ｄ×
○Ｂ − Ｃ× ×Ｂ − Ｃ○
○Ｂ − Ｄ× ○Ｂ − Ｄ×
○Ｃ − Ｄ× ○Ｃ − Ｄ×
従って、Ａ，Ｂ，Ｃ，Ｄの並べ替えを考えると、この場合、
２×４＝８通り
存在する。
確率分布表を書くと、
| １位のチーム数 | １ | ２ | ３ |
|---|---|---|---|
| 確率 | ｐ１ | ｐ２ | ｐ３ |
と表せる。
(1)〜(4)より、
ｐ１=24×(1/2)6+8×(1/2)6=32/64従って、１位のチーム数の期待値は、
ｐ２=24×(1/2)6=24/64
ｐ３=8×(1/2)6=8/64
１×ｐ１＋２×ｐ２＋３×ｐ３ =32/64+48/64+24/64 =104/64=13/8 （答）
| NO.1524 | 2005.3.16. | Junko | 鳩の巣の問題・その後(2) |
ご指摘どうもありがとうございました。
誤解をしていた部分をきちんと整理していただきました。
選ぶ数の個数が５０個だとすると、「偶数を５０個選んだ場合」に
どの２つをとっても最大公約数が１にはなりません。
では、５１個ならば？
「５１個の中に少なくとも奇数が１つ含まれてしまう。」ということは言えても、
それだけで最大公約数が１となる２数の存在は言えませんね。
解答その７、８のような示し方をしないとだめということですね。
勉強になりました。
| NO.1525 | 2005.3.30. | 水の流れ | 和算家の問題 |
先日、「第８回和算に学ぶ」会に出席したところ、次の問題が紹介されました。
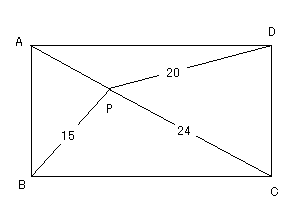
図のような長方形ＡＢＣＤの周および内部の点Ｐから各頂点に至る長さをＢＰ＝１５，ＣＰ＝２４，ＤＰ＝２０
とするとき、次の問に答えよ。
問題１：ＡＰの長さを求めよ。
問題２：長方形の面積の最大値を求めよ。また、そのときの２辺の長さも求めよ。
問題３：長方形の面積の最小値を求めよ。また、そのときの２辺の長さも求めよ。
E-mail
戻る