NO.1675 連勝連敗の平均 2007.5.21 水の流れ
第191回数学的な応募問題
皆さん、今年のゴールデンウィーク中にプロ野球セリーグは9連戦が行われました。
このときチームによって連勝や連敗が多く起きました。
巨人の場合は××○○○×○○×、横浜は○○○雨○○××○、
中日は×××××○○○×、阪神は×××雨××××雨、広島は○○○×○○○○雨、
ヤクルトは○○×○××××○でした。ここで、連勝連敗という連続数の平均を考えました。
例えば、巨人の場合は(2+3+1+2+1)÷5=1.8 です。
ここで次のような問題を作成しました。皆さん!考えてください。
あるチームがn(n≧2)試合野球を行ったとき、この連続数の平均の期待値を求めてください。
ただし、勝敗の起こる確率は5分5分とし、引き分けはないものとします。
問題1:n=2、3、4のときの期待値を求めよ。
問題2:一般のときの期待値をnで表せ。
注:この記事に関する投稿の掲載は、2007年6月11日以降とします。
NO.1674 階段の昇り方(2) 2007.5.21 夜ふかしのつらいおじさん
設問1
a1=1 は明らかです。
a2=2 は1段ずつ昇る場合と、2段で昇る場合があります。
a3=3、a4=4
・(111)、(12)、(21)
・(1111)、(112)、(121)、(211)
設問2
15段昇るのは、次の場合があります。
・すべて1段ずつ、15C1=1通り
・2段が1回、14C1=14通り
・2段が2回は、(212) の3ヶ所に「1」を10回入れる重複組み合わせを数えます。
3H10 =12C10= 66通り
・2段が3回は、(21212) の4ヶ所に「1」を7回入れる重複組み合わせの数を数えます。
4H7 = 10C7 = 120通り
・2段が4回は、(2121212) の5ヶ所に「1」を4回入れる重複組み合わせの数を数えます。
5H4 = 8C4 = 70通り
・2段が5回は、(212121212) の6ヶ所に「1」を1回入れる組み合わせの数を数えます。
6C1= 6通り
∴ 1+14+66+120+70+6=277通り
設問3
(n+2)段目に来るには、(n+1)段目からの場合とn段目からの場合があります。
ただし、n段目に来るのに最後は、1段昇りでなければなりません。
もし2段昇りで来ると2段昇りが連続してしまいます。
だから、n段目まで来るのには、an-1 通りの方法があることになります。
∴ an+2=an+1+an-1 ・・・ (1)
設問4
| n | 1 | 2 | 3 | 4 | 5
| 6 | 7 | 8 | 9 | 10
| 11 | 12 | 13 | 14 | 15
|
|---|
| an | 1 | 2 | 3 | 4 | 6
| 9 | 13 | 19 | 28 | 41
| 60 | 88 | 129 | 189 | 277
|
|---|
一つ手前と三つ手前の値を足せば求まります。
設問5
設問3の漸化式(1)を解いてみます。
両辺にαan+1とβanを加えます。
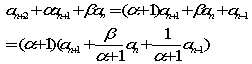
ここで
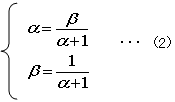
とすると、An=an+2+αan+1+βan は、
初項が a3+αa2+βa1で公比が(α+1)の等比数列です。
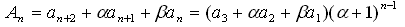
一般項を求めるには、(2)から導かれる次の3次方程式をとかねばなりません。
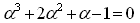
(2)の解を、α1、β1、α2、β2、α3、β3とします。
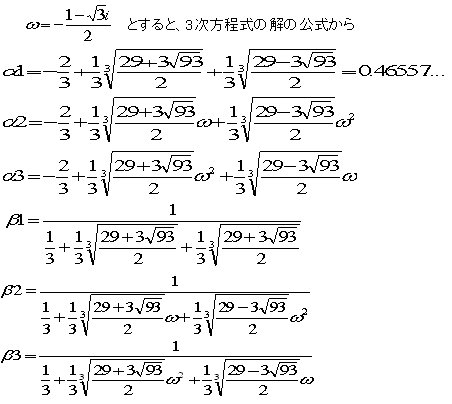
これらの数値をもちいて
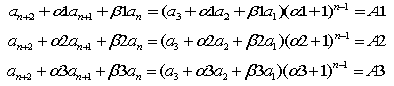
A1-A2より
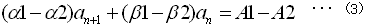
A2-A3より
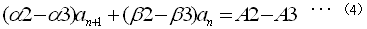
(3)×(α2-α3)-(4)×(α1-α2)より
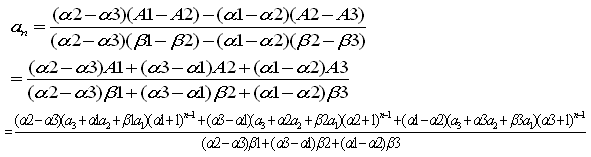
となりますが、具体的な数値で書き直すのは面倒なので省略します。
NO.1673 連続根号数の極限値の不思議 2007.5.16 K.F.
連続根号数の形をした関数(式.1)について考える。
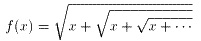 ・・・式.1
・・・式.1
「コロキウム室 NO.1598」のT.ヴィジャヤラガヴァンの定理により、
f(x)は、x≧0 のとき、極限値が存在する。
そこで、x=0 のときの f(x)の値を考える。
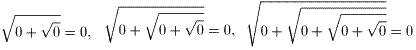
であるから、当然
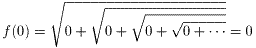
となると予想される。ところが、x が 0 の近傍のときの f(x) の値を計算すると、
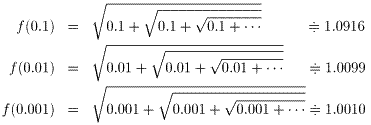
となり、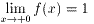 が強く予想される。
が強く予想される。
一方、「コロキウム室 NO.1622」から、
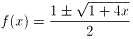 ・・・式.2
・・・式.2
であることが明らかである。式.2に x=0 を代入すると、 f(x)=0,1 となる。 以上のことから、f(0)=0 、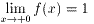 は両方とも正しいと
考えられる。すなわち、関数 f(x) は、x=0 の点で不連続である。
は両方とも正しいと
考えられる。すなわち、関数 f(x) は、x=0 の点で不連続である。
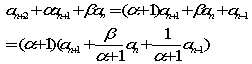
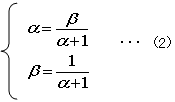
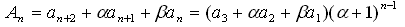
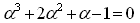
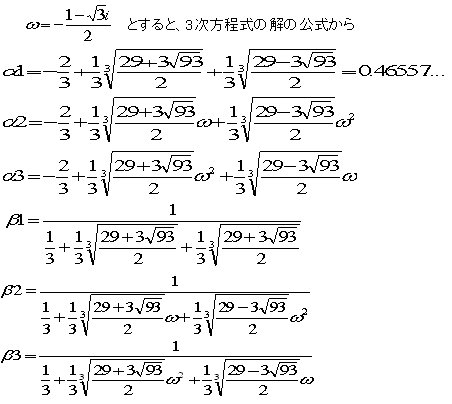
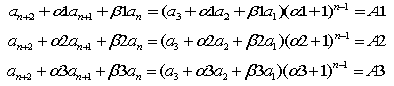
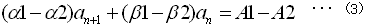
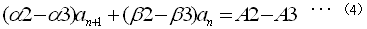
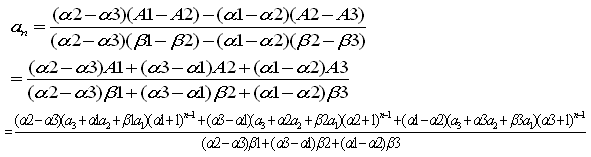
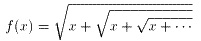 ・・・式.1
・・・式.1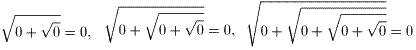
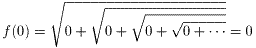
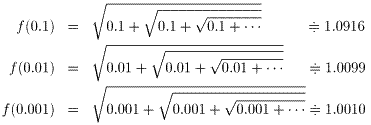
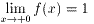 が強く予想される。
が強く予想される。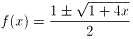 ・・・式.2
・・・式.2