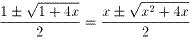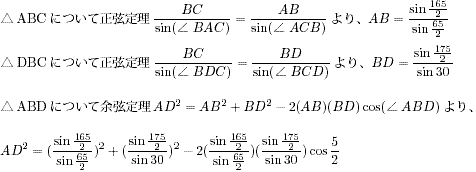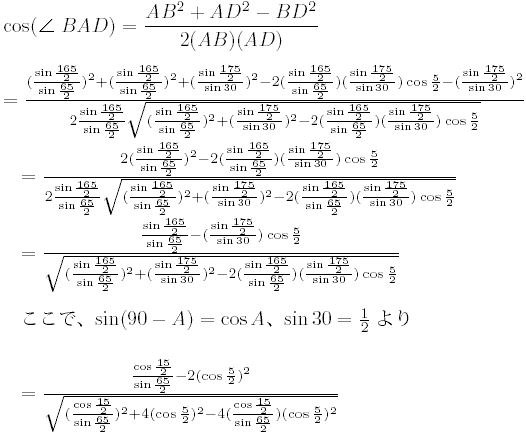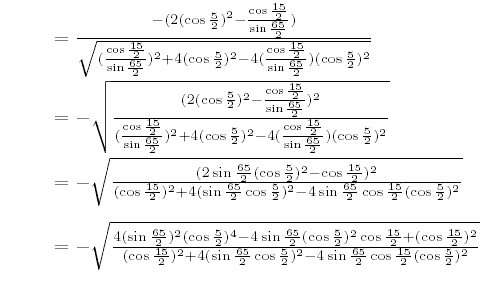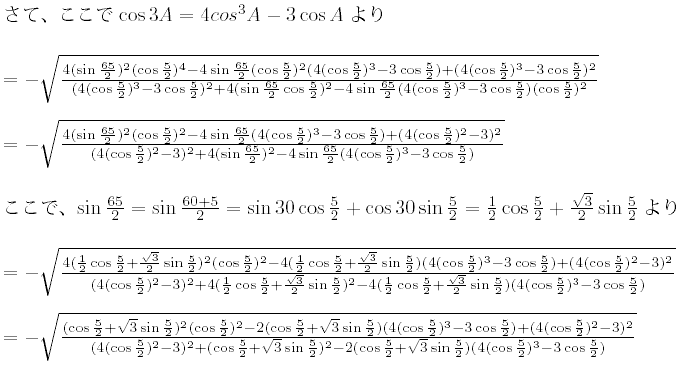NO.1627丂丂栺悢偺屄悢(4)丂丂2006.11.17.丂丂K.F.
栤戣侾丗
帺慠悢値偺惓偺栺悢偺屄悢乮d(n)偱昞偡偙偲偲偡傞丅乯偲丄 an偺抣傪幚嵺偵媮傔偰傒傞偲丄tab.1偺傛偆偵側傞丅tab.1
| n |
侾
|
俀
|
俁
|
係
|
俆
|
俇
|
俈
|
俉
|
俋
|
10
|
11
|
12
|
13
|
14
|
15
|
16
|
17
|
18
|
19
|
20
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d(n) |
侾
|
俀
|
俀
|
俁
|
俀
|
係
|
俀
|
係
|
俁
|
係
|
俀
|
俇
|
俀
|
係
|
係
|
俆
|
俀
|
俇
|
俀
|
俇
|
| an |
侾
|
侽
|
侽
|
係
|
侽
|
侽
|
侽
|
侽
|
俋
|
侽
|
侽
|
侽
|
侽
|
侽
|
侽
|
16
|
侽
|
侽
|
侽
|
侽
|
| n |
21
|
22
|
23
|
24
|
25
|
26
|
27
|
28
|
29
|
30
|
31
|
32
|
33
|
34
|
35
|
36
|
37
|
38
|
39
|
40
|
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| d(n) |
係
|
係
|
俀
|
俉
|
俁
|
係
|
係
|
俇
|
俀
|
俉
|
俀
|
俇
|
係
|
係
|
係
|
俋
|
俀
|
係
|
係
|
俉
|
| an |
侽
|
侽
|
侽
|
侽
|
25
|
侽
|
侽
|
侽
|
侽
|
侽
|
侽
|
侽
|
侽
|
侽
|
侽
|
36
|
侽
|
侽
|
侽
|
侽
|
| n |
41
|
42
|
43
|
44
|
45
|
46
|
47
|
48
|
49
|
50
|
|---|---|---|---|---|---|---|---|---|---|---|
| d(n) |
俀
|
俉
|
俀
|
俇
|
俇
|
係
|
俀
|
10
|
俁
|
俇
|
| an |
侽
|
侽
|
侽
|
侽
|
侽
|
侽
|
侽
|
侽
|
49
|
侽
|
栤戣俀丗
tab.1偐傜丄倎値亖値偲側傞傛偆側値偼暯曽悢偱偁傞偙偲偑椶悇偱偒傞丅徹柧
壖偵 n 偑暯曽悢偱偁傞偲偡傞丅
偡傞偲丄n 偼慺場悢p1丄p2丄丒丒丒丄pm丄偍傛傃帺慠悢
k1丄k2丄丒丒丒丄km偵傛傝丄
丂丂丂n=(p1k1丒p2k2丒丒丒
pmkm)2
=p12k1丒p22k2丒丒丒
pm2km丂丂丂乮幃.1乯
偲昞偝傟傞丅偙偺偲偒丄n偺惓偺栺悢偺屄悢d(n)偼丄
丂丂丂d(n)=(2k1+1)丒(2k2+1)丒丒丒(2km+1)丂丂丂乮幃.2乯
偱偁傞丅偝傜偵丄
丂丂丂(婏悢)亊(婏悢)亊丒丒丒亊(婏悢)=(婏悢)丂丂丂乮幃.3乯
偲側傞偐傜丄幃.2丄3傛傝丄
丂丂丂乽n偑暯曽悢偱偁傟偽丄n偺惓偺栺悢偺屄悢偼婏悢偱偁傞丅乿(柦戣.A乯
偼惓偟偄丅
堦曽丄幃.3偐傜傢偐傞傛偆偵丄媡偵婏悢傪場悢暘夝偡傞偲丄偦傟傜偺場悢偼偡傋偰婏悢偲側傞
乮嬼悢偺場悢偑擖偭偰偄傟偽丄婏悢偵側傜側偄丅乯偐傜丄柦戣.A偺乽媡乿傕惉傝棫偮丅
屘偵丄惓偺栺悢偺屄悢偑婏悢偱偁傞n偼丄昁偢暯曽悢偱偁傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮徹柧廔傢傝乯
栤戣俁丗
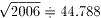 偱偁傞偐傜丄2006埲壓偺嵟戝偺暯曽悢偼丄
442=1936偱偁傞丅
偱偁傞偐傜丄2006埲壓偺嵟戝偺暯曽悢偼丄
442=1936偱偁傞丅暯曽悢偺榓偺岞幃丗
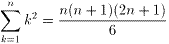 丂丂乮幃.4乯
丂丂乮幃.4乯傛傝丄
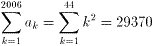
栤戣係丗
幃.4傛傝丄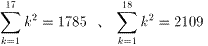 丂偑丄
偦傟偧傟媮傑傞丅
丂偑丄
偦傟偧傟媮傑傞丅
丂丂丂182亖324丄1+4+9+丒丒丒+324=2109
傛偭偰丄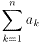 丂偑丄2006埲壓偲側傞傛偆側
n偺嵟戝惍悢偼丄323
丂偑丄2006埲壓偲側傞傛偆側
n偺嵟戝惍悢偼丄323
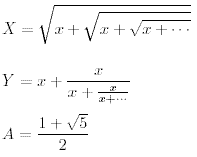
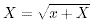 丒丒丒(1)
丒丒丒(1)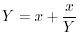 丒丒丒(2)
丒丒丒(2)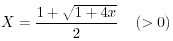 丒丒丒(3)
丒丒丒(3)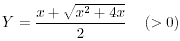 丒丒丒(4)
丒丒丒(4)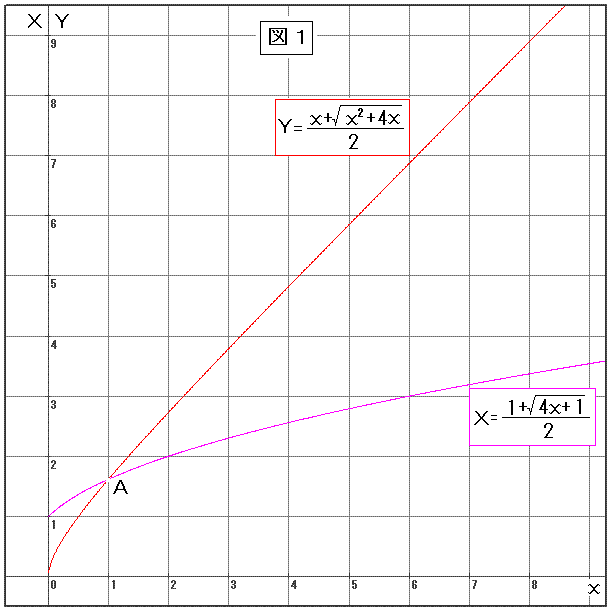
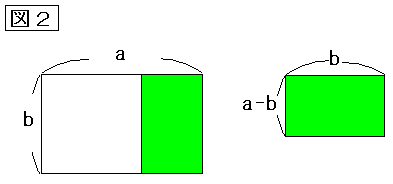
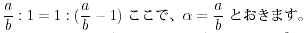
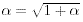 丒丒丒(5)丂傑偨偼
丒丒丒(5)丂傑偨偼
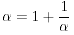 丒丒丒(6)
丒丒丒(6)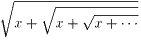 丂丂丂乮幃丏侾乯
丂丂丂乮幃丏侾乯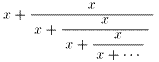 丂丂丂乮幃丏俀乯
丂丂丂乮幃丏俀乯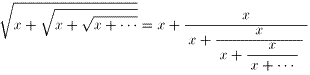 丂丂丂乮幃丏俁乯
丂丂丂乮幃丏俁乯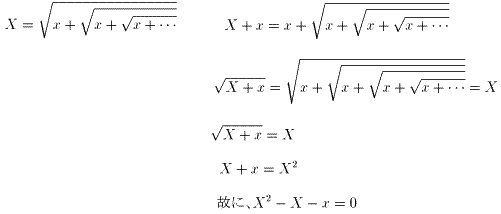 丂丂丂乮幃丏係乯
丂丂丂乮幃丏係乯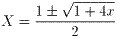 丂丂丂乮幃丏俆乯
丂丂丂乮幃丏俆乯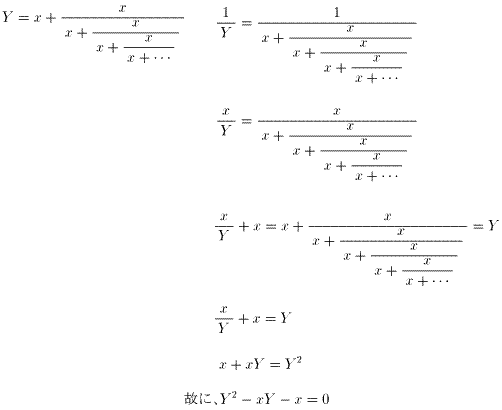 丂丂丂乮幃丏俇乯
丂丂丂乮幃丏俇乯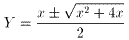 丂丂丂乮幃丏俈乯
丂丂丂乮幃丏俈乯