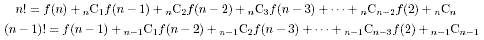NO.1668 重力による位置エネルギー 2007.3.19 DDT
同じ「おしえてＢＰ！」ねたです。
次の質問に出会いました。
タイトル：
重力による位置エネルギー
質問文 ：
ある物体(質量ｍ）を手のひらにおいて高さ０から１ｍに加速度なしで移動したとき、
物体がされる仕事は、上向きを正と考えて、手が物体にした仕事
Ｗ＝Ｆｄ＝ｍｇ*１（ジュール）
となり、物体がされた仕事はｍｇ*１（ジュール）となるみたいですが、
実際は重力も物体にはたらいているので、重力がぶったいにした仕事
Ｗ＝-Ｆｄ＝-ｍｇ*１（ジュール）
となり、物体がされた正味の仕事は
ｍｇ*１−ｍｇ*１＝０
となって、物体がされた正味の仕事が０なら、
物体は重力による位置エネルギー（＝ｍｇ*１）をもっているということにに矛盾すると、
ふと、考えてしまいました・・・。
この場合正味の仕事に「重力がぶったいにした仕事」は入ってない、
とかんがえるのでしょうか？
これを読んだ瞬間、私には反論一つ思い浮かびませんでした。
普通こういう議論は、運動方程式を直接距離で積分してやってしまうので、
逆にこういったストレートな疑問をぶつけられると、
応えようとして舌を噛んじゃいそうになります。どういう回答が出たかということで、リンクを挙げます。
QNo.2792960
しかしながら、私は上記回答のどれにも納得できませんでした。
それで、この投稿に及びました。
話は飛びますが、最近「ガリレオの指，ピーター・アトキンス，斉藤隆央訳，2004年12月，早川書房」
というのを読みました。
この本自体は、大人向けのブルーバックスといったところですが、
これに「いい事書いてるな！」と思える一文がありました。それは、
・仕事はエネルギーではない．
・仕事は、エネルギーの移動を表すものである．
がそれです。この言葉を使って「重力による位置エネルギー」の質問者の思いを述べると、
次のようになる気がします。
・手から質点へ、エネルギーｍｇ*１が仕事として移動した（追加された）．
・それと同時に重力により、質点から−ｍｇ*１のエネルギーが仕事として移動した（奪われた）．
・よって、正味のエネルギー変化は、ｍｇ*１−ｍｇ*１＝０となり、質点のエネルギーは増えない！．
（手で仕事を加えたにも関わらず！）
非常に素直な意見で、目が眩みそうになります。かなり長く考えた後、
やっと思い至ったのが次の点です。
「重力により、質点から−ｍｇ*１のエネルギーが仕事として移動した」のですが、
それはどこへでしょう？。手から加えた仕事は「手から質点へ」であり、
出発点と終着点がはっきりしています。しかし、
重力の仕事は、「質点からどこへ？」です。質点を引っ張る「地球へ」でしょうか？。
作用・反作用の法則があるので、思わず納得しかけますが、ちょっと考えれば、そうでない事に気づきます。
もうお気づきの方々は一杯いらっしゃると思うのですが、
以下では、数式で考えれば自明なことを、敢えて日常の言葉で述べます。まず例を挙げます。
(1) 重力が、質点のエネルギーを減らさない例
当たり前なんですが、自由落下がそうです。地面からある高さhにいる質点は、
その支えを失ったら自由落下を始めます。
このとき、重力「−ｍｇ」によってエネルギーの移動は起きますが、
それは質点の位置エネルギーから運動エネルギーへの移動であって、
[力学的エネルギー]＝[位置エネルギー]＋[運動エネルギー]
は、一定です（当たり前ですが・・・）。
では、質点を手によって持ち上げる場合はどうでしょうか？。
それを考えるために、加速度０でなく、高さh1の地点から、高さh2の地点へ、
質点を投げ上げる場合を見てみます。
(2) 質点を投げ上げる場合
実際には複雑な過程になりますが、高さh1で、質点は手から初速度v0を
（運動エネルギー1/2･mv02）を受け取ったとします。
質点は手から離れた瞬間から、重力によりエネルギーの移動を起こします。
質点の運動エネルギーから位置エネルギーへ。
高さh2でちょうど全ての運動エネルギーは位置エネルギーに移動し終わり、
速度０になるとします。その瞬間に、高さh2の地点で、質点に手を添え、支える事ができるはずです。
この状態は、高さh1から高さh2へ、ゆっくり（加速度０で）質点を持ち上げたのと同じ状態です。
ここから何が言えるかというと、
・手は質点に、仕事により運動エネルギーを追加した（まさに系に手を加えた）．
・重力は仕事により、質点の運動エネルギーを位置エネルギーに移した（奪ったのではない）．
・従って、手の仕事＋重力の仕事＝０ではあるが、質点のエネルギーは、手が加えた分だけ増えた．
・以上により、仕事はエネルギーではない事がわかる．
が言えます。
(3) ゆっくり（加速度０で）質点を持ち上げた場合
これは、無限にゆっくりした質点の投げ上げになります。
持ち上げる過程の各瞬間で小刻みに、(2)が起こっていると考えられます。
以上が私の、質問「重力による位置エネルギー」に対する回答になりますが、
先の質問は非常にもっともなものに思えました。
理由は二つあって、一つは仕事はエネルギーではない事を、
あまりはっきりとは教えてもらっていないこと。
もう一つは、古典力学の内部にいる限り、位置エネルギーの実体が見えない事に起因する気がします。
少なくとも古典力学にとどまる限り、ポテンシャルエネルギーは物理量ではないので、
位置エネルギーの実体といった言い方には、微妙な話が付きまとうのですが、
相対論にまで行けば、運動エネルギーも位置エネルギーも質量を（実体を）持ってくるとだけ、
ここでは言います。いずれにしろそのために、古典力学ではエネルギーの定義は
（特に位置ポテンシャルエネルギーが）、非常に操作主義的かつ実証主義的です。
先に挙げた本によれば、力学的エネルギーを最初に提唱したのはイギリスのヤングですが、
その定義はブリユアンが提唱した操作主義そのものに見えます。実際そこでは（同書pp.118〜120）、
「エネルギーとは、仕事をする能力である」
とされます。少し視点を拡げると、山崎義隆はその著書「重力と力学的世界」の中で
「資本主義とプロテスタント倫理」で有名な社会学者マックス・ウェーバーを引き合いに出し、
こうも言います（原文に忠実ではありません）。
「人は電車に乗るとき、その動作原理など何一つ気にせず安心して電車に乗る。 電車がどのように動作するかを知っているだけだ。 この原則として予測により未来は決定可能であるということ、 その確信を持つ事こそが合理化であり、世界の魔術からの解放である（マックス・ウェバー）」
続けて山崎氏は言います。
「物理学もそうやって近代化してきた。何故力が伝わるのか等の疑問を積極的に却下し、 どのように伝わるかのみを追及してきた。これはとても奇妙な事ではあるが、 その結果、技術的適用可能性が開け、重力は何故伝わるのかは何一つ知らないくせに、 それがどのように伝わるかだけでもって、人間は人工の天体を飛ばした（古典力学により）」
エネルギーの定義−マックス・ウェーバーの合理化−山崎義隆の物理学の近代化を並べてみると、
先の質問は、その延長線上に当然のように生まれて来るであろう疑問に思えます
（なんか昔の民生みたいですね）。
何を言いたいかというと「古典力学の中には、エネルギーの実体は存在しない」という事です。
だから先の疑問に応えるには、(1)〜(3)のような地を這うような操作主義的説明でなければ、
本当の了解は得られないのではないか？、と思えます。
特に位置エネルギーがそうです。運動エネルギーは、目に見えて物体が飛んでくので、
まだしもわかり易いですが、ポツネンと止まっているだけの物体全てが位置エネルギーを持つ、
という事は、じつはとてもわかりにくい事ではないかと思いました。
何故なら、実体の無い運動エネルギーと位置エネルギーの間で、あたかもそれらが存在するかのように
（存在するんですけど）、仕事をやりとるすると考えなければならないからです。
それらが何らかの形で（数式以外で）目に見えれば、両エネルギーは移動するだけで、
全体は不変だという構図は、もっと感覚的にはわかりやすかったのにな、と実感しました。
でも古典力学は、十分な理由の基に、そうやって発展してきました。
無いものねだりは、しても仕方ありませんね。
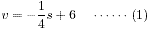
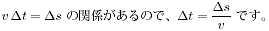
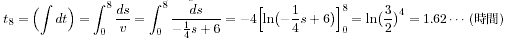
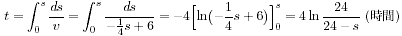
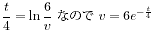
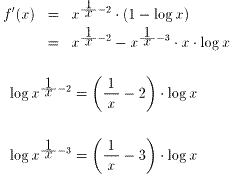
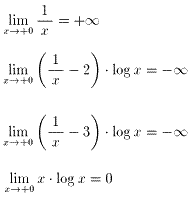
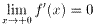
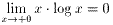は公式を用いました。） 
