NO.1655 たけしのコマネチ大学数学科 2007.2.18 Junko
フジテレビの木曜日深夜(1時15分から45分)に、
たけしのコマネチ大学数学科
という番組があるのをご存知でしょうか? こんな時間帯に数学の番組があるなんて、ちょっとびっくりです。
2月22日深夜(実際は23日)の放送で、
「プレゼントの問題」を
取り上げるということで、番組内に「Weekend Mathematics」のテロップ
が入ることになりました。
起きている自信はないので、ビデオ撮りすることにします。
ColloquiumNO.215
|
フジテレビの木曜日深夜(1時15分から45分)に、
たけしのコマネチ大学数学科
という番組があるのをご存知でしょうか? こんな時間帯に数学の番組があるなんて、ちょっとびっくりです。
2月22日深夜(実際は23日)の放送で、
「プレゼントの問題」を
取り上げるということで、番組内に「Weekend Mathematics」のテロップ
が入ることになりました。
起きている自信はないので、ビデオ撮りすることにします。
最近平均について、面白い講義を受けました。バーコフの個別エルゴード定理に関することです。
でもその前に、ポアンカレの再帰定理の話があります。
1.測度と可測集合に関する注意
以下の話では、測度と可測集合という言葉を度々使いますが、自分は測度論の初歩というか、
誰でもが知っている事しか知れません。よって以下で、測度,可測集合と言い出したら、
次のようなものを指していると、割り引いて読んで下さい。
測度の定義
集合X上の測度Pとは、Xから実数Rへの写像P:X→Rで、次の条件を満たすもの。
(1) P(φ)=0。ここでφは空集合.
(2) AとB⊂Xで、A∩B=φなら、P(A∪B)=P(A)+P(B).
(3) P(X)<∞.
可測集合
X上の測度Pに関する可測集合全体Βとは、A⊂Xとして、
(1) A=φである.
(2) A≠φなら、P(A)≠0である.
を満たすA⊂Xの全体Βのこと。特に、(2)を満たすA⊂Xが一つでも存在すれば、Xは可測集合になります。
以上のような、アマチュアの範囲です。
2.力学におけるポアンカレの再帰定理
次の定理は、アーノルドの「古典力学の数学的方法」に載っているものなので、本当です。
古典力学におけるポアンカレの再帰定理
Xを質点系の配位空間とし(n個の質点なら、R3nの部分集合)で、X⊂R3nは有界とする。
このとき、Xの任意の点の任意の近傍Uについて、有限時間の内にUに戻ってくる、x∈Uが存在する。
[証明]
古典力学を問題にしているので、x∈Xの時間発展は運動方程式に従う(微分方程式に支配される)。
ただし1秒後のxの位置をT(x)と表した場合、k秒後の位置はTk(x)で表す。1.5秒後とかも同様とする。
A⊂Xの時間発展を考えた場合、Aの時間発展は微分方程式に従うので、微分方程式の一般論から、
T:X→Xは単射である。よって、
A=T-1(T(A)) (a)
が成り立つ。またTが運動方程式の流れを表すという事から、
V(A)=V(T(A)) (b)
も成り立つ。ここでVは、領域AやT(A)の体積(測度)です。この結果はリュービルの定理と言われます。「古典力学の数学的方法」の中で実際に証明されています。
UをXの任意の点の任意の近傍とした場合、X⊂R3nなので、V(U)>0です。Uについて、次の無限列を考えます:
U,T(U),T2(U),T3(U),・・・
しかも、任意のi,j∈Nについて、
Ti(U)∩Tj(U)=φ
と仮定します。1.の測度の定義(2)と、この証明の式(b)より、
V(U∪T(U)∪T2(U)∪T3(U)∪・・・)
=V(U)+V(U)+V(U)+V(U)+・・・ (c)
です。ところがX⊂R3nは有界なので、V(X)<∞より、式(c)は、いつかはV(X)<∞を越えます。
従って、あるk,l∈N(k≧l)があり、
Tk(U)∩Tl(U)≠φ
となる必要があります(1.の測度の定義(2)から)。よって式(a)より、
Tk-l(U)∩U≠φ
が得られます。ここで、
x∈Tk-l(U)∩U⊂U
とすれば、
Tk-l(U)∈U
は明らかです。即ち(k−l)秒後に、x∈Uは、Uに戻ります。
[証明終]
3.複雑系におけるポアンカレの再帰定理
じつは受けた講義は「カオス・フラクタルを目指して」という趣旨だったのですが、
その準備として、ポアンカレの再帰定理を紹介されました。本当の事を言うと、
この部分は聞いていなかったのですが、後で期末レポートを出題されて、
ポアンカレの再帰定理を焼き直せる事に気づきました。まず、セッティングは以下となります。
セッティング:
X: 状態空間(何らかの集合)。Xの点は可測な近傍の基本系を持つとする.
Β: Xの可測集合全体.
T: X上の可測変換で、点x∈Xの時間発展を表し、Tは微分方程式に支配されるとする.
従ってTは、微分方程式の流れを表すので、単射.
P: Tに関する不変測度で、P(X)<∞.
ポアンカレの再帰定理
A∈Β,P(A)>0(A≠φ)とする。Aにある密集合Dがあり、任意のx∈Dについて、
xの軌道{Tnx}は、無限回Aに戻る。
補題1.
任意のA⊂Xについて、A=T-1(T(A))とP(A)=P(T(A))が成り立つ。
[証明]
Tが単射だから。[証明終]
補題2.
Xの任意の点の任意の近傍Uに関して、Uには、その軌道が十分長い時間の内に再びUに戻ってくる、
点x∈Uが存在する。ただしXの点は、可測な近傍の基本系を持つので、P(U)>0である。
[証明]
力学における再帰定理の証明と同じ[証明終]
補題3.
補第2の点x全体D'は、Xで密。
[証明]
補題2が、Xの任意の点の任意の近傍で言えるから。[証明終]
ポアンカレの再帰定理の証明.
A∈Β,P(A)>0(A≠φ)とする。Aにある密集合Dがあり、任意のx∈Dについて、
xの軌道{Tnx}は、無限回Aに戻る。
[証明]
A⊂Xは明らか。AにXからの導入位相を定義すれば、密集合の推移性より、
補題2のD'はAでも密。それをD=A∩D'とすれば良い。
無限回戻るのは、補題2(古典力学の再帰定理)のTk-l(x)を出発点として、何回でも繰り返せるから。[証明終]
4.ポアンカレの再帰定理を解釈すると
アーノルドの「古典力学の数学的方法」に載っていた再帰定理では、Tは運動方程式の流れを表し、
リュービルの定理から、ルベーグ測度PがT不変となっています。
このときPは体積を表し、Tは体積不変な写像です。当然全空間Xは有限体積を持ち、
Xの有界性が本質にあります。しかし焼き直しによれば、X上の測度Pが有界性を持てば、
Xに有界性を要求しなくても再帰定理が成り立ちます(大筋では正しいと思います)。
x∈Xの軌道が無限の彼方に飛び去れば永遠に帰ってこない事を考えると、
これは、測度Pの有界性と可測性(任意のA∈ΒでP(A)>0)が、
結果としてXに有界性を課すように思えます。もちろん再帰時間と、
その時点までに観測されたXの拡がりが、時間とともにじりじり拡大する事は考えられますが。
ここで測度Pを観測と考え、また観測には確率も含まれるとすれば、以上の事は普通の言葉で言えば、
「一度でも見れたものは、何回でも見れる。何回でも起こる可能性がある」
(A∈ΒでP(A)>0) (P(A)=P(T(A)だから)
となるように思えます。一度でも見れた(A∈ΒでP(A)>0)とは、Xの有界性の現われです。
ここで問題になるのが、PがT不変である事です。例えばXを人間の社会や歴史とした場合、
Xの定常性は危ういので、Pの不変性は?です。しかし私はもともと土木出身ですが、
土木では大雨の再現確率を問題にして、河川計画などを行います。今まで再現確率は、
たんなる観測上の統計値にすぎないと思っていたのですが、じつはこんなところに成立根拠が潜んでいたのかも
しれないと考え直しました。
自然は人間よりもずっと定常性があるので、案外再帰定理が成り立つ格好のモデルになるような気はします。
ところで余談ですが、少なくとも気象に関しては、定常性が危うくなっているかもしれません。
理由は、もちろん理由は温暖化です。とはいえ、例えば宇宙論の最先端分野なんかを考えると、
自然はやっぱり定常的なのかもしれず、一般化された再帰定理は有効な気がします。
再帰定理について、もっと卑近な例を考えます。定常性ということで、
「三つ子の魂百までも」はどうでしょう?。Pを「三つ子の行動の再現確率」とした場合、
再帰定理はけっこう成り立ってる気がします。
5.エルゴード定理
これは証明できません。証明すると唱っていた講義の回も聞き逃しました。
でも、次のような定性論は間違いでしょうか?
これも定常性が成り立つという条件下と思いますが、
バーコフのエルゴード定理は、空間平均は時間平均に等しいです。次のような例を考えます。
私は現在プログラマーをやっています。プログラムには、非常に豊かに開発者の個性が現れます。
ところがプログラムにはBugがつきものです。Bugとは(間違い方とは)、
開発者の個性の発露でもあります。結果としてBugは、プログラマーの残業時間の最大の原因になります。
さらに残業は経験上、酒量の最大原因の一つです。
そこでR3に、点(Bugの発生回数,残業時間,酒量)を毎日プロットし、
「ddtの状態空間」をつくります。プロットを1年続ければ、「ddtの生活軌道」を描けます。
空間平均が時間平均に等しければ、この1年間の生活軌道の平均点のまわりで、
ddtは、向こう百年間うろうろしていることになります。何故ならddtには、
「三つ子の魂百までも」の定常性が成り立っているから、です。
「平均点のまわりでうろうろする」とは、再帰定理に見えます。もちろん平均は積分量なので、
全空間一様に生活軌道が拡がっていても平均は出るので、平均に再帰しやすいとは厳密には言えません。
しかし平均のまわりに正規分布するが、通説です。これを信じれば、定常性があれば、
軌道は平均に再帰しやすく、ある一瞬の観測結果をもって、
平均量については遥か未来まで見通せることになります。
このように考えると、初等的な統計量である平均という考えが、
通常思われているより、ずっと強力な道具なんだと気づかされます。
この問題は、1つの式で解答を得られます。
次のように、赤玉●がb個並んでいるとします。
1●2●3●4・・・b●b+1
白玉を入れることのできる場所が、(b+1)カ所あります。
白玉の入れ方の総数は、
重複を許して(b+1)個からa個組合わせるやり方の数 b+1Haです。
赤玉をすべて取り出す前に白玉を取り出し終わる場合の数は、
重複を許してb個からa個組合わせるやり方の数 bHaです。
だから求める確率は、
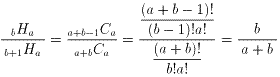
重複組み合わせについて
皆さん、教えてください。生徒から2005年椙山女学園大学の入試問題を質問されました。
下図について考える。これは次のようにして作図したものです。
まず点Oを中心とする半径5の円を描く。これに接線を引き、その接点をTとする。
次に、この接線と60゜の角度をなす直線で、円周に切り取られる長さが6であるものを描く。
この直線と円周の交点をA、Bとし、接線との交点をPとする。
このとき、PTの長さ、PBの長さと、△PBTの面積を求めよ。
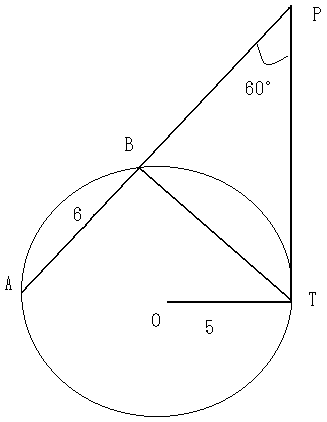
注:この記事に関する投稿の掲載は、2007年2月26日以降とします。
問題1
具体的に書き出して個数を数えます。
f(8,1)=8
( {1},{2},{3},{4},{5},{6},{7},{8} )
f(8,2)=21
( {1,3},{1,4},{1,5},{1,6},{1,7},{1,8},
{2,4},{2,5},{2,6},{2,7},{2,8},
{3,5},{3,6},{3,7},{3,8},
{4,6},{4,7},{4,8},
{5,7},{5,8},
{6,8} )
f(8,3)=20
( {1,3,5},{1,3,6},{1,3,7},{1,3,8},
{1,4,6},{1,4,7},{1,4,8},
{1,5,7},{1,5,8},
{1,6,8},
{2,4,6},{2,4,7},{2,4,8},
{2,5,7},{2,5,8},
{2,6,8},
{3,5,7},{3,5,8},
{3,6,8},
{4,6,8} )
f(8,4)=5
( {1,3,5,7},{1,3,5,8},
{1,3,6,8},
{1,4,6,8}
{2,4,6,8} )
問題2
1つおきに数を取っていくときがsの最大になります。
f(n,s) において
nが偶数のとき、1≦s≦n/2
nが奇数のとき、1≦s≦(n+1)/2
問題3
f(n,s)を具体的に数えて計算します。
F(1)=f(1,0)+f(1,1)=1+1=2
F(2)=f(2,0)+f(2,1)=1+2=3
F(3)=f(3,0)+f(3,1)+f(3,2)=1+3+1=5
F(4)=f(4,0)+f(4,1)+f(4,2)=1+4+3=8
F(5)=f(5,0)+f(5,1)+f(5,2)+f(5,3)=1+5+6+1=13
F(6)=f(6,0)+f(6,1)+f(6,2)+f(6,3)=1+6+10+4=21
F(7)=f(7,0)+f(7,1)+f(7,2)+f(7,3)+f(7,4)=1+7+15+10+1=34
F(8)=f(8,0)+f(8,1)+f(8,2)+f(8,3)+f(8,4)=1+8+21+20+5=55
この結果はパスカルの三角形のなかで次のような値を意味します。
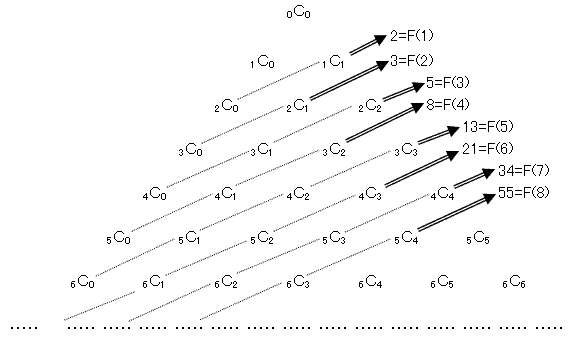
F(n)=f(n,0)+f(n,1)+f(n,2)+・・・+f(n,s-1)+f(n,s)
=n-(0-1)C0+n-(1-1)C1
+n-(2-1)C2+・・・+n-(s-1-1)Cs-1+n-(s-1)Cs
ここでF(n)の各項は、
f(n,s)=n-(s-1)Cs= 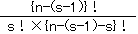
これについて例をあげて説明します。
例えば、f(8,3)=20を次のように考えます。
| 1 | {1,3,5} → oxoxoxxxX |
|---|---|
| 2 | {1,3,6} → oxoxxoxxX |
| 3 | {1,3,7} → oxoxxxoxX |
| 4 | {1,3,8} → oxoxxxxoX |
| 5 | {1,4,6} → oxxoxoxxX |
| 6 | {1,4,7} → oxxoxxoxX |
| 7 | {1,4,8} → oxxoxxxoX |
| 8 | {1,5,7} → oxxxoxoxX |
| 9 | {1,5,8} → oxxxoxxoX |
| 10 | {1,6,8} → oxxxxoxoX |
| 11 | {2,4,6} → xoxoxoxxX |
| 12 | {2,4,7} → xoxoxxoxX |
| 13 | {2,4,8} → xoxoxxxoX |
| 14 | {2,5,7} → xoxxoxoxX |
| 15 | {2,5,8} → xoxxoxxoX |
| 16 | {2,6,8} → xoxxxoxoX |
| 17 | {3,5,7} → xxoxoxoxX |
| 18 | {3,5,8} → xxoxoxxoX |
| 19 | {3,6,8} → xxoxxoxoX |
| 20 | {4,6,8} → xxxoxoxoX |
問題4
f(n,s)=n-(s-1)Cs
問題5
nが奇数のとき(n=2s-1)
| F(n)+F(n+1) | =f(n,0)+f(n,1)+f(n,2)+・・・+f(n,s-1)+f(n,s) |
| =f(n+1,0)+f(n+1,1)+f(n+1,2)+・・・+f(n+1,s-1)+f(n+1,s) | |
| =n-(0-1)C0+n-(1-1)C1+n-(2-1)C2+・・・+n-(s-1-1)Cs-1+n-(s-1)Cs | |
| +n+1-(0-1)C0+n+1-(1-1)C1+n+1-(2-1)C2+・・・+n+1-(s-1-1)Cs-1+n+1-(s-1)Cs | |
| = n+1C0+nC1 +・・・+n-s+2Cs-1+n-s+1Cs (あ) | |
| +n+2C0+n+1C1+nC2 +・・・+n-s+2Cs (同じ色のものを縦にまとめる) | |
| =n+2C0+n+2C1+n+1C2 +・・・+n-s+3Cs+n-s+2Cs+1(い) | |
| =n+3C0+n+2C1+n+1C2 +・・・+n-s+3Cs+n-s+2Cs+1 |
※ まとめるのは、nCr-1+nCr=n+1Cr
※ 最初の項は、組み合わせで取る個数が0なので左の添え字を変えても問題ない。
※ 最後の項について、(あ)の最後の式はsCs (い)の最後の式はs+1Cs+1となり値は等しい。
| F(n)+F(n+1) | =f(n+2,0)+f(n+2,1)+f(n+2,2)+・・・+f(n+2,s)+f(n+2,s+1) |
| =F(n+2) |
nが偶数のとき(n=2s)
| F(n)+F(n+1) | =f(n,0)+f(n,1)+f(n,2)+・・・+f(n,s) |
| =f(n+1,0)+f(n+1,1)+f(n+1,2)+・・・+f(n+1,s+1) | |
| F(n)+F(n+1) | =n-(0-1)C0+n-(1-1)C1+n-(2-1)C2+・・・+n-(s-1-1)Cs-1+n-(s-1)Cs |
| +n+1-(0-1)C0+n+1-(1-1)C1+n+1-(2-1)C2+・・・+n+1-(s-1)Cs+n+1-(s+1-1)Cs+1 | |
| = n+1C0+nC1 +・・・+n-s+1Cs | |
| +n+2C0+n+1C1+nC2 +・・・+n-s+1Cs+1 (同じ色のものを縦にまとめる) | |
| =n+3C0+n+2C1+n+1C2 +・・・+n-s+2Cs+1 | |
| =f(n+2,0)+f(n+2,1)+f(n+2,2)+・・・+f(n+2,s+1) | |
| =F(n+2) |
F(n)+F(n+1)=F(n+2)となりフィボナッチ数列になります。
t2=t+1とすると
t=(1±√5)/2なので
a=(1−√5)/2、b=(1−√5)/2とすると、まず
F(n+1)-bF(n)=a{F(n)-bF(n-1)}とおくと
F(n+1)-bF(n)は初項F(2)-bF(1)、公比aの等比数列なので
F(n+1)-bF(n)={F(2)-bF(1)}×an-1 ・・・ (1)
次に
F(n+1)-aF(n)=b{F(n)-aF(n-2)}とおくと
F(n+1)-aF(n)は初項F(2)-aF(1)、公比bの等比数列なので
F(n+1)-aF(n)={F(2)-aF(1)}×bn-1 ・・・ (2)
(1)-(2)より
(a-b)F(n)={F(2)-bF(1)}×an-1-{F(2)-aF(1)}×bn-1
これを整理すると
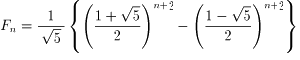
問4から書きます。
問4 f(n.s)=n+1−sCs
例えば10個から隣り合わない3つの数字を
選ぶことと8個から好きに3つの数字を選ぶことには1対1対応がつく。
好きに選んだ3つの数を(a,b,c)としたとき、(a、b+1、c+2)という写像をと
ればよい。
問5
a+bCb + a+bCb-1
=a+b+1Cbを使うと
F(n+2)=F(n+1)+F(n)
となりフィボナッチ数列となる。
一部修正(2007.3.4.)
カプレカ数という整数があります。
たとえば、
452=2025→20+25=45
552=3025→30+25=55
992=9801→98+ 1=99
のように、2乗した整数を”適当”に2つの整数に分割して和
をとると元の整数になるものです。
このカプレカ数が、どのような形になるかを考察しました。
まず定義から:
定義
kがカプレカ数である⇔∃n≧1,l≧0,10n>r≧1
:k=l+rかつk2=l×10n+r
kをカプレカ数とすると、「k=l+rかつk2=l×10n+r」であるので、
r=k−lをk2=l×10n+rに代入すると、
k2=l×10n+k−l
k×(k−1)=l×(10n−1) (1)
を得る。
逆にkを(1)を満たすの整数とすると、r=k−lとおくこと
により、
k2=l×(10n−1)+k
=l×10n+k−l=l×10n+r
を得るので、カプレカ数となる。
以上により、次の定理か成り立つ。
(定理)
kがカプレカ数である⇔∃n≧1:k×(k−1)/(10n−1)が整数である。
この定理により、カプレカ数の求め方が非常に楽になったので
ある。
(2/2 一部修正、追加)
高校生以上の数学の好きな人なら誰でも考えた(ている)不定方程式について述べます。
xy=yx (0<x<y) ・・・式.1
この不定方程式について、自然数解は、(x,y)=(2,4)に限られることは、勘の鋭い人なら
容易に想像できます。しかし、証明はそう簡単ではありません。
私は、高校生のときに確信していましたが、大学に入るまで証明できませんでした。
以下、証明を述べます。
証明
式.1は、
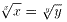 (0<x<y) ・・・式.2
(0<x<y) ・・・式.2
と同値である。よって、関数
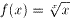 ・・・式.3
・・・式.3
の挙動について調べればよい。式.3を対数微分法によって、微分すると、
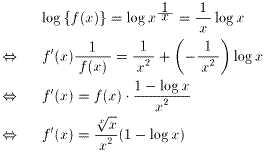 ・・・式.4
・・・式.4
が得られる。式.4から、次のi)からiii)が成り立つ。
| i) | 0<x<e | ←→ | f'(x)>0 |
| ii) | x=e | ←→ | f'(x)=0 |
| iii) | e<x | ←→ | f'(x)<0 |
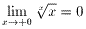
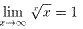 (証明は後述)であるから、
関数f(x)のグラフの概形を描くと、fig.1のようになる。
(証明は後述)であるから、
関数f(x)のグラフの概形を描くと、fig.1のようになる。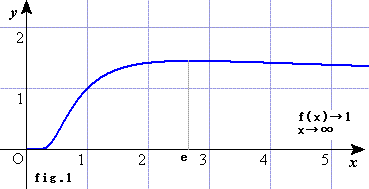
以上のことから、式.1の不定方程式の自然数解は、
(x,y)=(2,4)に限られることが証明される。
関数f(x)は、x=eのとき、極大かつ最大となる。
故に、fig.1から、式.2が成り立つならば、それはx>1の場合であることが明らかであり、
かつ1<x<e、e<yでなければならないことも明らかである。
しかも、1<x<eを満たす自然数は、x=2しかないのであるが、実際 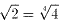 が成立している。
が成立している。
(証明終わり)
< 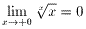 の証明>
の証明>
 (証明終わり)
(証明終わり)
< 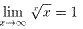 の証明>
の証明>
まず、 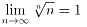 を証明する。
を証明する。
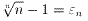 (n>1)とおく。
(n>1)とおく。
すると 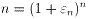 だから、二項定理により、
だから、二項定理により、
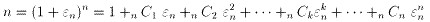 ・・・式.5
・・・式.5
が得られる。
式.5の右辺の各項は正だから、
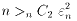 となり、
となり、 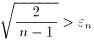 が成り立つ。
が成り立つ。
よって、 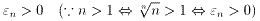 を考えると、
を考えると、
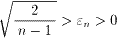 が成り立ち、
が成り立ち、 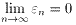 となる。
となる。
故に 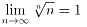 が成り立つ。
が成り立つ。
一方、式.4から、n≦x<n+1(n>2)のとき、関数f(x)は常に単調減少であり、
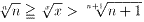 が成り立つ。
が成り立つ。
故に、 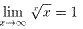 (証明終わり)
(証明終わり)
<補足>
関数f(x)は、x=eのとき、最大となるから、
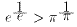
すなわち

であることがわかる。
ところで、式.4、fig.1から、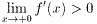 が明らかですが、極限値が求められません。
が明らかですが、極限値が求められません。
どなたかご存知の方がいたら教えてください。
<追記>
方程式 xx=yy (0<x<y)には、無限に多くの「実数解」が存在します。
高校生の方、対数微分法を使って、ぜひチャレンジしてみてください。
