NO.1659 プレゼントの問題(18) 2007.2.26 真夏のサンタ
プレゼントの問題に関して、１問出してみたいと思います。
何人かでプレゼントを交換したとき、自分のプレゼントを手に入れる人の数の期待値
はいくらになるでしょう？
結果は面白いなと思ったのですがきちんと証明ができないので、わかる方がいらっ
しゃれば教えてもらいたいです。
NO.1658 歩いた時間 2007.2.26 水の流れ
第１８７回数学的な応募問題
皆さんはウオーキングをしませんか。８ｋｍの距離を、最初の地点で時速６ｋｍ、
最後の到着地点では時速４ｋｍになり、途中の時速は、歩いた距離の1次関数で
表されるようにウオーキングするとき、歩いた時間を求めてください。
＜コメント：このウオーキングはまっすぐ歩いてください。後戻りは考えていません。＞
注：この記事に関する投稿の掲載は、２００７年３月１９日以降とします。
NO.1657 円と接線(3) 2007.2.26 まーや
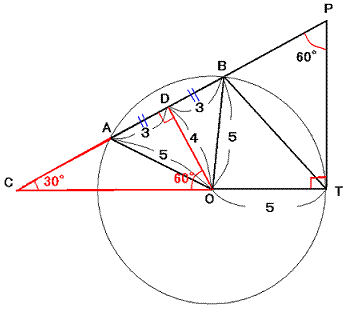
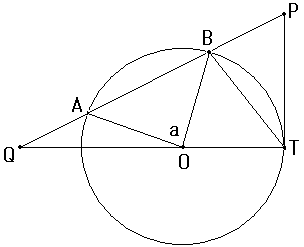
TOの延長線とPAの延長線の交点をCとする。
点OからABに向かって垂線を引き、その垂線とABの交点をDとする。
このときODは、線分ABの垂直二等分線となる。よって、
∠ODA＝90° AD＝DB＝AB×1/2＝6×1/2＝３
△PCTにおいて、∠CTP＝90°，∠TPC＝60°なので、
∠PCT＝30°
△OCDにおいて、∠ODC＝90°，∠OCD＝30°なので、
∠COD＝60°
（方針）
△PCTと△OCDが相似で、
内角が90°，60°，30°の直角三角形であることを利用して解く。
△ODAにおいて、AD＝３，OA＝５（円の半径）なので、
三平方の定理より OD＝４
△OCDは内角が90°，60°，30°の直角三角形なので、
OD：DC：CO＝１：√3：２
OD＝４より DC＝4√3 CO＝８
△PCTは内角が90°，60°，30°の直角三角形なので、
PT：TC：CP＝１：√3：２
TC＝TO＋CO＝５＋８＝13より
NO.1656 円と接線(2) 2007.2.26 夜ふかしのつらいおじさん
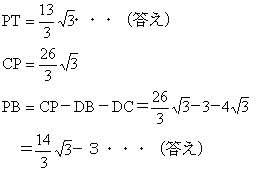
1
∠AOB＝a とおき、さまざまな角を a を用いて表します。
（角は直角を90度とする方法としますが単位を省きます）
∠ＢＡＯ＝90−a/2
∠OAQ＝90＋a/2
∠AQO＝30
∠QOA＝60−a/2
2
△OABにおいて正弦定理を使い角aの三角比の値を調べます。
AB/sin(∠AOB)a ＝OB/sin(∠BAO) より
6/sin a ＝ 5/sin(90-a/2)＝5/cos a/2
6･cos a/2＝5･sin a
36(1＋cos a)/2＝25(1−cos2 a)
25cos2 a＋18cos a−７＝0
(25cos a−７)(cos a＋1)＝0 より
cos a＝7/25
sin a＝24/25
ついでに半角の値も調べておきます。
cos2 a＝(1＋cos a)/2＝(1＋7/25)/2＝16/25
sin2 a＝(1−cos a)/2＝(1−7/25)/2＝9/25 より
cos a/2＝4/5
sin a/2＝3/5
3
QOの長さを調べ、QTの長さを求めます。
△OAQに正弦定理を使い
OA/sin 30＝OQ/sin(90＋a/2)＝OQ/cos a/2 より
OQ＝OA･cos a/2／sin 30＝5･(4/5)／(1/2)＝8 より
QT＝QO＋OT＝8＋5＝13
4
PTの長さを求めます。
△PQTにおいて、PT：QT＝1：√3なので、
PT＝QT/√3＝13/√3
5
AQの長さを調べ、QBの長さを求めます。
△OAQに正弦定理を使い
OA/sin 30＝ＱＡ/sin(60−a/2)＝ＱＡ/(sin 60･cos a/2−cos 60･sin a/2) より
QA＝5･(√3/2･4/5−1/2･3/5)／(1/2)＝4√3−3
QB＝QＡ＋ＡＢ＝4√3−3＋6＝4√3＋3
6
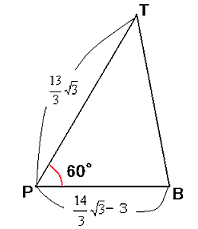
次にＰＱの長さを調べ、ＰＢの長さを求めます。
ＰＱ：ＰＴ＝2：1なので、
ＰＱ＝2･ＰＴ＝2･13/√3＝26/√3
ＰＢ＝ＰＱ−ＢＱ＝26/√3−(4√3＋3)＝14/√3−3
7
△ＰＢＴの面積Ｓを求めます。
Ｓ＝1/2･ＰＢ･ＰＴ･sin 60＝1/2･(14/√3−3)･13/√3･√3/2
＝13/4･(14/√3−3)
