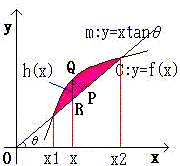

Weekend Mathematics/コロキウム室/1998.7~12/NO.18
NO.130 8/1 水の流れ 円に関する微分(11)
NO.115で提起した問題です。
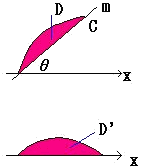
曲線C:y=f(x)と直線m:y=xtanθ で囲まれた図形を、
直線 m を 軸として回転して得られる立体の体積Vを求めよ。 (勿論、囲まれた図形がある場合)
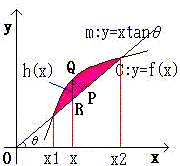 |
 |
 |

NO.131 8/1 水の流れ 円に関する微分(12)
NO.114で示した問題です。
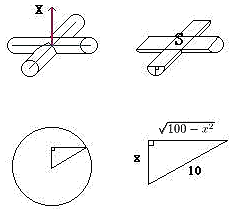
半径10㎝の2つの直円柱を直交させたとき、 交わりの部分の体積を求めてください。
 |
 |

NO.132 8/3 水の流れ 二等辺三角形の証明(1)
「三角形の二つの底角のそれぞれの二等分線を引き、それぞれの線が
対辺に交わる点までの長さが等しいとき、この三角形は二等辺三角形 であることを証明せよ」
勿論、三角関数を用いると高校生にも解けますが、中学生に解ける
ようにとのこと。
この問題はどこかで扱った覚えのある私は、広中平祐の
「学問の発見」(佼成出版社)という本の中にあったことを覚えて いました。広中先生は旧制中学校のとき、恩師の先生からの出題
でして、当時3,4通りの方法で時間を費やして解かれたと書いて ありました。
この本そのものは一読に値する本です。 学問に対しての「創造することの楽しさ、喜び」を伝えています。

NO.133 8/8 Junko ワンダ-数学ランド
8月3日~21日まで、NHK教育テレビの9:45~10:10で、
「ワンダ-数学ランド」という番組をやっています。
講師は秋山仁さんですが、実験や物作りを中心に数学の話
題に触れるということで、とてもおもしろいです。

NO.134 8/8 水の流れ 二等辺三角形の証明(2)
132の関連問題あり。
「3角形ABCにおいて、 ∠A,∠Bの2等分線が対辺と交わる 点を、それぞれ、D,Eとし、2等分線どうしの交点をPとする。

NO.135 8/10 水の流れ ジョギングの問題(3)
微分方程式に持ち込まなくても、積分でもできますので、紹介します。 <考え方> <解答>
所要時間=距離÷速さを考え、微小な所要時間を寄せ集めて、
全体の時間を得ることが積分の定義からでてきます。

生徒に出題すると、一部は平均時速が4.5kmより、
答えを2時間とする者もいます。
(この考えはいつも鮮やかなので、思い出に残っています。)

NO.136 8/11 美しい水 ナンプレ(1)
ナンプレを作りました。
1から9まで矛盾なく入れて、そこから決定されていく数字を消していきました。


NO.137 8/16 水の流れ 砂丘の問題(1)
「砂丘にいる私から直線状の道路の最短地点Pまでは、
2kmで、Pから道路上8kmの地点にホテルがある。
私は砂丘の上では毎時3km、道路上では毎時5km歩くことができます。
私が今いる地点から最短時間でホテルへ行くためには道路上Pから、
何km離れた道路上の地点をめざして歩けば良いですか。」
*誰か 教えて ください。


NO.138 8/17 Junko ナンプレ(2)
ナンプレに挑戦しました。しばし、楽しい時間でした。
解くのはともかく、作ってしまうというのはすごい!


NO.139 8/24 ヴァー 砂丘の問題(2)

このような問題は、たとえば「光は所要時間が最短になるような経路を進む」
という光学におけるフェルマーの原理に似ています。
フェルマーの原理は、数理的には変分法として広く用いられています。

NO.140 8/28 Junko 砂丘の問題(3)


 E-mail
E-mail
 戻る
戻る