| NO.1408 | 2003.9.5. | Junko | 價僼僅儞偺恓偺幚尡(6) |
FLASH ActionScript傪巊偭偨僔儈儏儗乕僔儑儞傪嶌偭偰傒傑偟偨丅

| NO.1409 | 2003.9.10. | 悈偺棳傟 | 晄掕曽掱幃 |
懢榊偝傫偼丄愭擔乽拞旜乿偝傫偐傜丄
乽懭墌嬋慄偺惍悢揰乿偺栤戣傪捀偒傑偟偨丅偦傟偱丄嫋戻傪摼偰丄崱夞偺栤戣偵偟傑偟偨丅
栤戣侾丗 晄掕曽掱幃x2-3y4=1偺惍悢夝(x,y)傪|x|,|y|<= 10偺斖埻偱扵偟側偝偄丅
寁嶼婡偑巊梡壜擻側傜丄|x|,|y|<= 100偺斖埻傑偱峀偘傞偲丄偳偆側傝傑偡偐丠
栤戣俀丗 晄掕曽掱幃x2-3y4=1偺惍悢夝(x,y)偼丄Q1偱媮傔偨傕偺偵尷傞偙偲傪帵偟側偝偄丅
栤戣俁丗 晄掕曽掱幃x2-3y4=1偺桳棟悢夝(x,y)偱丄惍悢夝偱偼側偄傕偺傪丄彮側偔偲傕侾屄尒偮偗側偝偄丅
栤戣係丗晄掕曽掱幃x2-3y4=1偺桳棟悢夝(x,y)偼柍悢偵懚嵼偡傞偙偲傪帵偟側偝偄丅

| NO.1410 | 2003.9.27. | DDT | 扨幩偲慡幩(4) |
侾丏NO.1343丂扨幩偲慡幩(1)偺忬嫷
wasmath偝傫偺嬄傞偲偍傝丄廤崌榑偵偍偗傞1懳1幨憸丆忋傊偺幨憸偲丄寳榑偺扨幩丆慡幩偺奣擮偼杮棃暿暔偱偡丅
偦偆側偺偱偡偑丄
丂丂嘆 寳榑偼傆偮偆巊傢側偄丏
丂丂嘇 扨幩丆慡幩偲偄偆梡岅偼丄尰傟偨偲偟偰傆偮偆廤崌榑偺撪晹丏
丂丂嘊 寳偺幩偵彮偟偱傕嬤偄摴嬶棫偰偼丄傆偮偆廤崌榑偺幨憸偟偐側偄丏
偲偄偆忬嫷偐傜乮傕偪傠傫愱栧怑偺曽乆偼彍偒傑偡乯丄偳偆偣幨憸偟偐巊傢傫偺偩偐傜丄
梡岅傪棳梡偟偰偟傑偊偲偄偆埨堈側婥帩偪偱丄NO.1343傪彂偒傑偟偨偑丄wasmath偝傫偺嬄傞偲偍傝偱偡丅
俀丏摼堄偺尵偄栿
偱丄NO.1343傪偳偆偄偆婥帩偪偱彂偄偨偐偲偄偆偲丄
NO.1348傪堷梡偡傟偽丄
乽侾懳侾幨憸乿傗乽忋傊偺幨憸乿偺傛偆偵廤崌偺梫慺偵埶懚偡傞偐偵巚偊傞奣擮偑丄 乽扨幩乿傗乽慡幩乿偲偄偭偨 廤崌(object)偲幨憸(morphism)偺傒偵埶懚偡傞奣擮偲偟偰婯掕偱偒傞 偲偄偆偙偲偱偡丅 偙傟偼偛偔堦晹偱偡偑丄杮幙傪拪徾偟偰榞慻傒偩偗偱榑偠傜傟傞偲偙傠偑寳榑偺埿椡偲枺椡偩偲尵偊傑偡丅
榞慻傒偩偗偱榑偠傜傟傞偲偙傠偑寳榑偺埿椡偲枺椡側偺偼丄慺恖偺惓捈側巚偄偲偟偰偼丄 偠偮偼晄婥枴偱偡丅廤崌偺梫慺偵埶懚偡傞偐偵巚偊傞奣擮偑丄 廤崌(object)偲幨憸(morphism)偺傒偵埶懚偡傞奣擮偲偟偰婯掕偱偒傞 偐傜偱偡丅偳偆偟偰廤崌偲幨憸偺傒偵埶懚偟偰婯掕偱偒傞偺偐丠丄偦偺嬶懱揑側叶平扪傪抦傝偨偄両丄 偲偄偆偺偑丄巹偲巹偺桭恖偺偦傕偦傕偺摦婡偱偟偨丅偱傕偦偙偵摜傒崬傓偺偼丄 傗偭傁傝杮枛揮搢側傫偱偟傚偆偐丠
埲壓NO.1343偺巹側傝偺夝摎傪弎傋傑偡丅戝妛帪戙偵悢妛壢偱傕側偄偔偣偵丄 弶傔偰寳榑傪憡庤偵偡傞偲偄偆偙偲偱丄廤崌偺梫慺傊偺埶懚傪偱偒傞偩偗攔彍偡傞曽恓偱丄 嬯怱嶴滈偺寢壥偱偡丅偦偺傇傫慺恖偭傐偄偱偡丅
栤侾丏
憸偲媡憸傪巊偭偨丄扨幩丆慡幩偺掕媊丅
扨幩偺掕媊
f丗倃仺倄丆y伕f(倃)偲偡傞丅f-1(y)亖{x}偺偲偒丄f傪扨幩偲偄偆丅
偙偙偱{x}伡倃偼丄梫慺偑x偺傒偺1揰廤崌傪昞傢偡丅
慡幩偺掕媊
f丗倃仺倄偲偡傞丅f(倃)亖倄偺偲偒丄f傪慡幩偲偄偆丅
栤2丏
掕棟1.
丂丂(1) f偑扨幩 佁 嵍媡幨憸偑偁傞丅
丂丂(2) f偑慡幩 佁 塃媡幨憸偑偁傞丅
偺徹柧丅徹柧偺偨傔偵師偺娙扨側曗戣偲掕媊傪帵偡丅
曗戣1.
f丗倃仺倄丆y1偲y2伕倄偲偡傞丅y1亗 y2側傜丄
f-1(y1)伩f-1(y2)亖冇偑惉傝棫偮丅
乵徹柧乶
f-1(y1)伩f-1(y2)亗冇傪壖掕偡傞偲丄
恾-1傛傝丄嫟捠暘偺1揰偐傜2杮偺懳墳偺栴偑偨偪丄f偼幨憸偱側偔側傞偺偱丄偙傟偼晄壜丅
廬偭偰f-1(y1)伩f-1(y2)亖冇偑昁梫丅
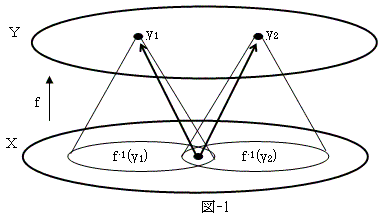
廬偭偰恾-2偵帵偡傛偆側丄幨憸偺昗弨暘夝偑惉傝棫偮丅
掕媊7.幨憸偺昗弨暘夝乮挻戝嶨攃側掕媊乯
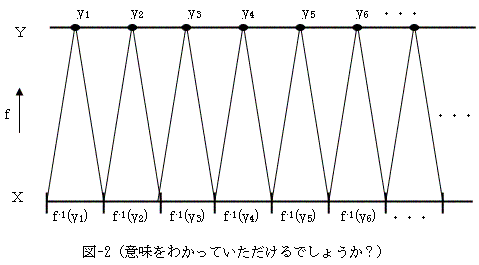
掕棟1.偺徹柧
丂丂(1) f偑扨幩 佁 嵍媡幨憸偑偁傞丅
乵徹柧乶
丂丂嵍媡幨憸偑偁傞 佀 f偼扨幩
f丗倃仺倄丆r仜f亖IdX偲側傞 r丗倄仺倃偑懚嵼偡傞偲偡傞丅
r仜f偺昗弨暘夝傪恾-3偵帵偡丅
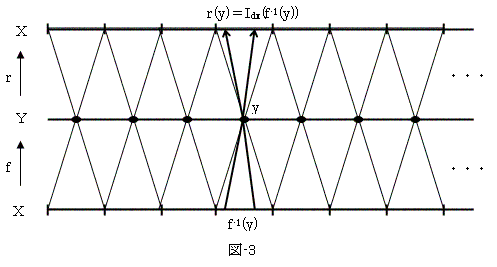
傕偟f-1(y)偑1揰廤崌偱側偄偲偡傞偲丄恾-3偵帵偟偨傛偆偵丄
y伕f(倃)偵偍偄偰2杮埲忋偺-1(y)傊偺懳墳偺栴偑偨偮丅
壗屘側傜丄r偺掕媊傛傝r(y)亖Idx(f-1(y))亖f-1(y)偩偐傜丅
r偼幨憸偱側偔側傞偺偱丄偙傟偼晄壜丅廬偭偰f-1(y)偼1揰廤崌偑昁梫丅傛偭偰f偼扨幩丅
f偑扨幩 佀 嵍媡幨憸偑偁傞
傕偟f偑憃幩側傜丄r偲偟偰f-1傪偲傟偽椙偄偙偲偼偁偒傜偐丅
偙偙偱f-1偼丄f偑憃幩偩偭偨応崌偺f偺媡幨憸偱丄f-1偼f偵偮偄偰堦堄偵掕傑傞丅
偦偙偱丄抣堟傪倄偐傜f(倃)偵堏峴偡傞偙偲偵傛偭偰丄f偐傜摼傜傟傞幨憸丄
丂丂丂丂f'丗倃仺f(倃)乮f'丗x 乥仺 f(x)乯
傪掕媊偡傞丅f'偼f偺抣堟傪f(倃)偵嫹傔偨偩偗偺傕偺偱乮偙傟偼彑庤偵偱偒傞乯丄柧傜偐偵慡幩丅
傑偨f偼傕偲傕偲扨幩偩偭偨偐傜丄f'偼憃幩偲側傝丄媡幨憸丄
丂丂丂丂f'-1丗f(倃)仺倃
偑懚嵼偡傞丅f'-1仜f'亖Idx偼柧傜偐偩偑丄
f'-1仜f亖Idx傕傎傏帺柧偱偁傞乮恾-4乯丅
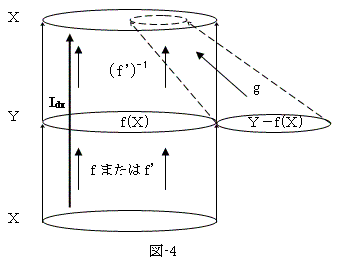 恾-4偱偼丄f(倃)偲倄亅f(倃)偲偑屳偄偵慺側廤崌側偺偱丄抍巕忬偵暘棧偟偰彂偄偨丅
恾-4偱偼丄f(倃)偲倄亅f(倃)偲偑屳偄偵慺側廤崌側偺偱丄抍巕忬偵暘棧偟偰彂偄偨丅
f'-1偼f'偵偮偄偰堦堄偵掕傑傝丄f'偼f偐傜堦堄偵掕傑傞偐傜丄
寢嬊f(倃)忋偱f'-1仜f亖Idx傪枮偨偡f'-1丗f(倃)仺倃偼丄f偐傜堦堄偵掕傑傞丅
傛偭偰倄忋偱r仜f亖Idx傪枮偨偡r丗倄仺倃偼丄f(倃)偱偼f'-1偵堦抳偟側偗傟偽側傜側偄丅
偮傑傝f'-1偺掕媊堟傪倄傑偱墑挿偟偰傗偭偨傕偺偑丄媮傔傞r偩丅
偲偙傠偑偙偺墑挿偼丄擟堄偵峴偭偰椙偄丅幚嵺恾-4傛傝丄
f(倃)偐傜倄傊偺掕媊堟偺墑挿晹暘倄亅f(倃)偵丄f偵傛偭偰倃偐傜幨憸偟偰偔傞倃偺憸偼側偄丅傛偭偰丄
丂丂丂丂g丗倄亅f(倃) 仺 倃
傪倄亅f(倃)偐傜倃傊偺擟堄偺幨憸g偲偟偰丄
丂丂丂丂r亖f'-1伨g
偲偡傟偽丄
丂丂丂丂r仜f亖(f'-1伨g)仜f
亖(f'-1仜f)伨(g仜f)
亖(f'-1仜f)伨冇
亖f'-1仜f亖Idx
偲側傝丄f偑扨幩側傜嵍媡幨憸偑懚嵼偡傞丅
[徹柧廔傢傝乶
(2) f偑慡幩 佁 塃媡幨憸偑偁傞丅
乵徹柧乶
塃媡幨憸偑偁傞 佀 f偼慡幩
f丗倃仺倄丆f仜s亖IdY偲側傞 s丗倄仺倃偑懚嵼偡傞偲偡傞丅
f偼s偺嵍媡幨憸偵側偭偰偄傞偐傜丄s偼扨幩偱偁傞丅
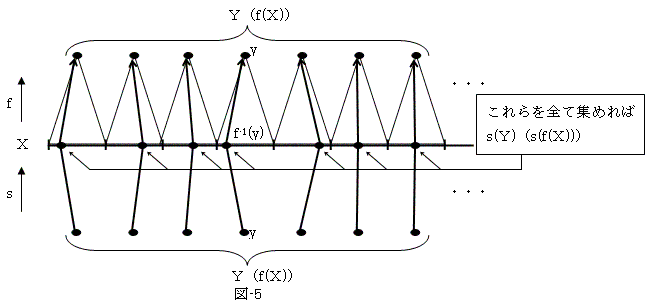
f仜s偺昗弨暘夝傪恾-5偵帵偡丅
f仜s亖IdY偩偐傜恾-5傛傝丄f(s(倄))亖倄偱側偗傟偽側傜側偄丅
s(倄)伡倃偩偐傜丄倄亖f(s(倄))伡f(倃)丅堦曽f(倃)伡倄偼帺柧偩偐傜丄f(倃)亖倄丅
偡側傢偪f偼慡幩丅
f偑慡幩 佀 塃媡幨憸偑偁傞
f偑昁偢偟傕慡幩偱側偄偲偟偰丄恾-5偵傛偆偵s傪掕傔傞偲丄
f仜s偼
峆摍幨憸Id丗f(倃)仺f(倃)偲側傝丄s偼s丗f(倃)仺倃丅
偄傑f偼慡幩偩偐傜Id亖IdY偱偁傝丄f偑慡幩側傜塃媡幨憸偑懚嵼偡傞丅
[徹柧廔傢傝乶
栤3丏
塃媡幨憸傪巊偭偨丄憃幩偺摿挜偯偗
乵夝摎乶
尵梩偵偡傞偲傂偳偔摉偨傝慜側偺偩偗傟偳丄偙偆側傞丅
丂丂丂丂慡幩側f偺塃媡幨憸偑f偵偮偄偰堦堄偵掕傑傞偲偒丄f偼憃幩丅
側傫偱摉偨傝慜偐偲偄偊偽丄f偑憃幩側傜媡幨憸f-1偑偁傝丄
f-1仜f亖IdX
傕f仜f-1亖IdY傕惉傝棫偪丄
s亖f-1偲偍偗偽椙偔丄
f-1偑f偵偮偄偰堦堄側偺偼柧傜偐偩偐傜丅偦傟偱傕忬嫷傪愢柧偡傞偲丄偙偆側傞丅
恾-5傛傝塃媡幨憸s偼丄慡幩側f偑偁偭偨偲偒s丗y乥仺x偐偮x伕f-1(y)偲掕媊偡傟偽傛偄偙偲偑傢偐傞丅
偙偺x偼f-1(y)偺梫慺偱偁傝偝偊偡傟偽椙偄偺偱丄s偼堦斒揑偵偼堦堄偵掕傑傜側偄丅
x偑嫮惂揑偵桞堦偵側傞偨傔偵偼丄f-1(y)亖{x}偲1揰廤崌偱偁傞昁梫偑偁傞丅偙傟偼f偑扨幩傪堄枴偟丄
f偼慡扨幩偱憃幩丅
摨條偵扨幩側f偺嵍媡幨憸r偑f偵偮偄偰堦堄偱偁傞偨傔偵偼丄恾-4偱倄亅f(倃)亖冇偑昁梫丅
偙偺偲偒f亖f'偲側傝丄r亖f'-1亖f-1偱f偼憃幩丅
栤4.
埲壓傪帵偣丅
侾丏扨幩
f偑扨幩偱偁傞忦審偼丄
倃偲倄偲倅傪擟堄偺廤崌丆f偲g偲h偼幨憸偱丄f丗倃仺倄丆g偲h丗倅仺倃偲偟偰丄
丂丂丂丂f仜g亖f仜h
側傜昁偢g亖h偲側傞偙偲丅
俀丏慡幩
f偑慡幩偱偁傞忦審偼丄
倃偲倄偲倅傪擟堄偺廤崌丆f偲g偲h偼幨憸偱丄f丗倃仺倄丆g偲h丗倄仺倅偲偟偰丄
g仜f亖h仜f
側傜昁偢g亖h偲側傞偙偲丅
乵徹柧乶
侾丏扨幩
倃偲倄偲倅傪擟堄偺廤崌丆f偲g偲h偼幨憸偱丄f丗倃仺倄丆g偲h丗倅仺倃偲偟偰丄
丂丂丂丂f仜g亖f仜h
側傜昁偢g亖h偵側傞偲偡傞乮埲屻丄忦審-1偲屇傇乯丅
抣堟傪倄偐傜f(倃)偵堏峴偡傞偙偲偵傛偭偰f偐傜摼傜傟傞幨憸丄
丂丂丂丂f'丗倃仺f(倃)
傪掕媊偡傞丅f偵懳偟偰忦審-1偑惉棫偡傞側傜丄f'偵懳偟偰傕丄
f'仜g亖f'仜h 佀 g亖h 偑惉棫偡傞偙偲偼柧傜偐丅
f'偼慡幩側偺偱塃媡幨憸偑偁傞丅偦偙偱倅亖f(倃)偲偟丄2偮偺塃媡幨憸s1偲s2傪乮恾-6乯丄
g亖s1偲h亖s2偍偗偽丄
丂丂丂丂f'仜g亖f'仜s1亖Id倅
亖f'仜s2亖f'仜h
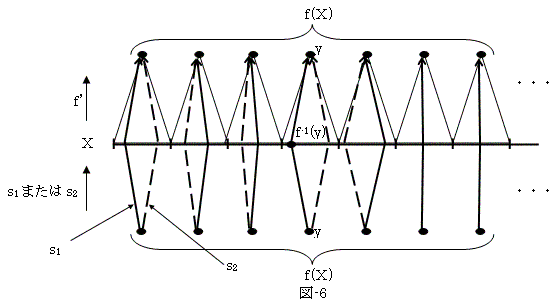
側偺偱丄f'仜g亖f'仜h偑惉傝棫偮丅
忦審-1傛傝g亖h偲側傝丄s1亖g亖h亖s2偐傜s1亖s2偲側傞丅
偙傟偼慡幩側f'偺塃媡幨憸s偑丄f'偵偮偄偰堦堄偱偁傞偙偲傪帵偡丅
傛偭偰f'偼憃幩丅f'偑憃幩偲偄偆偙偲偼丄掕媊偐傜f偼彮側偔偲傕扨幩丅
媡偵f偑扨幩側傜嵍媡幨憸r偑偁傞偐傜丄
丂丂丂丂r仜f仜g亖r仜f仜h
丂丂丂丂IdX仜g亖IdX仜h
丂丂丂丂g亖h
偑惉傝棫偮丅
俀丏慡幩
倃偲倄偲倅傪擟堄偺廤崌丆f偲g偲h偼幨憸偱丄f丗倃仺倄丆g偲h丗倄仺倅偲偟偰丄
丂丂丂丂g仜f亖h仜f
側傜昁偢g亖h偵側傞偲偡傞乮埲屻忦審-2偲屇傇乯丅
y伕f(倃)偲偟丄廤崌f-1(y)伡倃偺堦揰s(y)伕 f-1(y)偐傜y伕倄傊偺幨憸f'傪掕媊偡傞
乮恾-7乯丅偙傟偼f偺掕媊堟偺弅彫偵側偭偰偍傝丄恾-7偲恾-5傪尒斾傋傟偽丄恾-7偑丄
f(倃) 忋偺塃媡幨憸s傪掕媊偱偒傞偺偼柧傜偐偱偁傞丅偦偙偱f'偺掕媊堟傪s(f(倃))偲彂偔丅
偝傜偵丄f偵懳偟偰忦審-2偑惉棫偡傞側傜丄
f'偵偮偄偰傕g仜f'亖h仜f' 佀 g亖h偑惉傝棫偮偺偼柧傜偐丅
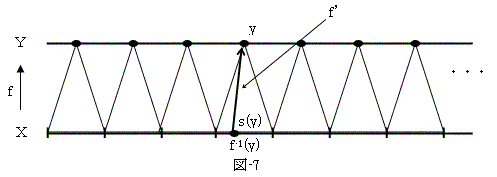
恾-7傛傝f'偼扨幩偱偁傞丅倅亖s(f(倃))偲偟丄g仜f'亖h仜f'偺
g偲h傪f'偺2偮偺嵍媡幨憸r1偲
r2偲偡傞丅
偙偺偲偒丄
丂丂丂丂g仜f'亖r1仜f'
亖Id倅亖r2仜f'亖h仜f'
側偺偱丄g仜f'亖h仜f'偑惉傝棫偮丅忦審-2傛傝g亖h偲側傝丄
r1亖g亖h亖r2偐傜r1亖r2偲側傞丅偙傟偼扨幩側f'偺嵍媡幨憸r偑丄
f'偵偮偄偰堦堄偱偁傞偙偲傪帵偡丅傛偭偰f'偼憃幩丅f'偑憃幩偲偄偆偙偲偼丄掕媊偐傜f偼彮側偔偲傕慡幩丅
媡偵f偑慡幩側傜塃媡幨憸倱偑偁傞偐傜丄
丂丂丂丂g仜f仜s亖h仜f仜s
丂丂丂丂g仜IdY亖h仜IdY
丂丂丂丂g亖h
偑惉傝棫偮丅

| NO.1411 | 2003.9.28. | 悈偺棳傟 | 帺慠悢夝 |
愭擔峴傢傟偨戞係係夞崙嵺悢妛僆儕儞僺僢僋乮俬俵俷乯擔杮戝夛偱丄
擔杮慖庤偺惉愌偼嬥儊僟儖侾屄丄嬧儊僟儖俁屄丂摵儊僟儖俀屄偱偟偨丅
傑偨丄惉愌忋埵崙丂侾埵丂僽儖僈儕傾丂俀埵丂拞崙乮枮揰侾恖乯丂俁埵丂傾儊儕僇丂
係埵丂儀僩僫儉乮枮揰俀恖乯丂俆埵丂儘僔傾丂俇埵丂娯崙丂俈埵丂儖乕儅僯傾丂俉埵丂僩儖僐丂
俋埵丂擔杮偲戝寬摤偱偟偨丅
偦偙偱丄棃擭弌応偟偨偄偲偄偆堄梸偵偁傞奆偝傫偵丄師偺傛偆側栤戣傪採嫙偟傑偡丅
栤戣侾丏師偺摍幃傪枮偨偡帺慠悢偺慻乮倎丄倐丄們乯傪偡傋偰媮傔傛丅
丂丂丂丂乮侾亄侾乛倎乯亊乮侾亄侾乛倐乯亊乮侾亄侾乛們乯亖俀
偨偩偟丄侾乛倎偼倎偺媡悢偺偙偲偱偡丅
栤戣俀丏師偺摍幃傪枮偨偡帺慠悢偺慻 乮倎丄倐乯偼懚嵼偟側偄偙偲傪帵偟側偝偄丅
丂丂丂丂倎俀亅俀倐俀亖侽

 E-mail
E-mail
 栠傞
栠傞