
Weekend Mathematics/コロキウム室/NO.143
| NO.1221 | 2002.6.1. | おっくん | ピタゴラスの定理(1) |
こんばんわ!わからないことがあるのでおしえてくださいませ!

| NO.1222 | 2002.6.2. | Junko | ピタゴラスの定理(2) |
ピタゴラスの定理を満たす自然数の組み合わせは整数倍を除いていくつぐらいあるか
? という質問かと思います。答えは無限です。その作り方も含めて、
問題3 らせん階段の問題
のまとめの部分に記述がありますので、参考にしていただければと思います。

| NO.1223 | 2002.6.2. | DDT | 不正な処理とラッセルのパラドックス |
1.ラッセルのパラドックス
任意の集合を考えた場合、その集合は、
自分自身をその要素として含むか含まないかのどちらかである。
ふつうの集合では、自分自身は部分集合としては自明に含まれるが、
自分自身をその要素としては含まない。
そこで、自分自身をその要素として含まない集合の集合を考える。
定義1
自分自身をその要素として含まない集合の集合を、Aとする。
定理(ラッセルのパラドックス).
集合Aは、矛盾する。
[証明]
(1)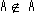 の場合
の場合
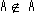 であれば、Aは要素として自分自身を含まないので定義1より、
A は Aに属する。従って、
であれば、Aは要素として自分自身を含まないので定義1より、
A は Aに属する。従って、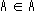 でなければならない。
でなければならない。
(2)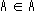 の場合
の場合
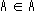 であれば、AはAに属するので定義1より、Aは要素として自分自身を含まない。
従って、
であれば、AはAに属するので定義1より、Aは要素として自分自身を含まない。
従って、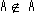 でなければならない。
でなければならない。
(3)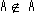 であり、かつ
であり、かつ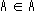 でもある。従って、これは矛盾。
でもある。従って、これは矛盾。
[証明終わり]
このじつにすっきりしたパラドックスは、文字列という物理的実体と、
文字列の並び方から発生する意味とを区別しないために起こるスコーレムの逆理や、
必ず嘘つくクレタ人のパラドックス,対角線論法につながることは容易に見てとれます
(なんとなくですが)。問題は、集合Aが既存のものを集めただけでは済まない集合だ、
という点です。
定義1にある、自分自身をその要素として含まない集合とは、自然数全体の集合Nや、
Nの要素一つ一つを部分集合として{1},{2},・・・と並べ立ててやったものなどが全て含まれ、
少なくとも数学的にはそれらはみな存在が保証されます。
つまり既存の集合です。これらを集めることには問題ありません。
ところが集合Aも、定義1によれば集合なので、自分自身をその要素として含まない
集合か否かを判定する必要が生じます。
これを行わないと、集合Aの要素を全て集め切ったことにならないからです。
しかしAに対してその判定を行うためには、A自身ともいえる定義1に戻るしかありません。
Aは既存のものでなく、定義1によって初めて生じたものだからです。
ある集合を定義するとき、自分自身まで要素判定の対象になることは、ふつう絶対にありません。
いいかえれば、既存のものだけ集めればいいように、集合はふつう構成されます。
自然数全体の集合Nの定義はこうです。
定義2(自然数全体の集合)
有限基数のことを自然数といい、自然数全ての集まりを、自然数全体の集合と呼ぶ。
言葉で言うと恐ろしく虚しいのですが、この虚しさが安全の秘密です。
有限基数や自然数全ての集まりが、既存の集合として存在することは、定義2の外で保証されます。
定義2の役目は、自然数全ての集まりに、自然数全体の集合という名前をつけることに尽きます。
すでにあるものに名前を付けるだけなので、この時点で、自然数全体の集合は有限基数か?
などと問われることは、絶対にありません。これらの問題はそれ以前に決着がついてます。
つまり定義とは、本当に術語の定義でなければいけないのです(通常の公理的集合論では、たぶん)。
定義1のように、ある定義が新しい集合を生成する事態を、自己参照型宣言と呼んでおきます。
なぜ自己参照かは、要素判定はその定義を根拠とするしかないからです。
定義を型宣言と言い直したのは、数学の世界の定義が、
プログラミングの世界の型宣言に相当するからです。
2.プログラミングの世界における型宣言と定義
プログラミングの世界の型宣言とは次のようなものです。C/C++,FOTRAN,Visual Basic(VB)では、
構造体(ユーザー定義型),クラスなどと言われるものが造れます。
例えば、平面直角座標の点をたくさん扱いたい場合は、Cood_XYという勝手な名前の、
新しい変数型(データ型)を宣言します。
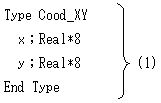
(1)は構造体またはユーザー定義型といわれるものの例で、
C/C++とFOTRANとVisual Basicの書式がごっちゃになってますが、
Cood_XY型の型宣言です。Typeは型の意,Cood_XYはその名前(タグ名ともいいます),
Type〜End TypeまででCood_XY型が2つの実数xとyの組であることを表し、
;Real*8はxやyが実数型であることと言ってます。
次に定義ですが、(1)でCood_XY型を宣言しただけでは、まだCood_XY型の変数は使えません。
Cood_XY型の変数が存在しないからです。それらを存在させるためには、
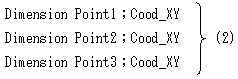
とやります。Point1;Cood_XYは、Point1という変数名を持つCood_XY型の変数を表し、
先頭のDimensionは、Point1をメモリ上に生成してくれとコンピューターに頼んでます。
コンピューターが(2)を読んだ時に、Point1,Point2,Point3という操作可能な変数が、
コンピューター内部に出現します。これを定義といいます。
C/C++であれば演算子のオーバーロードができます。例えば2項演算子 + の意味を拡張して
Point3 = Point1 + Point2
に、ベクトル計算の意味を割り当てられます。このように構造体やクラスは自由度が高いので、
複雑で巨大なプログラムには多用されます。実際WindowsというOSは、クラスと構造体のお化けです。
ここで重要なのは、型宣言(1)が既存の型(実数型)だけで構成される点です。
実数も扱えないようなコンピューターは存在意義がないに等しいので、実数型,整数型,
文字列型はどんな言語でも、あらかじめ使えるようになってます。
つまり実数型,整数型,文字列型は型宣言せずにDimensionできるという意味です。
型宣言(1)の外部で、実数,整数,文字列の集合の存在は保証されるといっても同じです。
メモリ上に変数を生成するとは、メモリ素子のいくつかの集団をその変数の記憶領域とすることです。
これは集合の実体化だといえます。(1)では8バイトの実数2個の組となり、Point1やPoint2には
16バイト=16×8個のメモリ素子が割り当てられます。そしてその集団がどんな内部構造を持つ
必要があるのかについて、コンピューターは型の名前で判断し、内部構造の情報は、
型の名前が一致する型宣言から読み取ります。型の名前がタグ名と言われる由縁であり、
型宣言とは、数学における通常の術語定義と同じものであることもわかります。
プログラミングの世界では、自己参照型宣言は厳密に拒否されます。例えば、
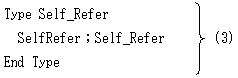
のような型宣言です。C/C++では、無名構造体の名のもとに(3)に似た型宣言もできるのですが、
定義の部分で自己参照はうまく回避されます。
普通のコンパイラーなら(3)でただちにエラーを出します。頭のいいコンパイラーなら、
(3)をあっさり無効と判断した上で、
Dimension SelfRefer;Self_Refer
を型指定なしのDimensionだとみなし、あらかじめ使える型から2バイト整数くらいを選んで
SelfRefer用にメモリをマップして、実行時には何食わぬ顔で0を代入し続けるようにコンピューター
には動作仕様書を送り付けるかもしれません(EXEファイルのこと)。
ところが変数定義時のデフォルト値指定オプションという(余計な?)機能が存在します。
これは明示的に変数への値の代入が行われないならば、Dimension時の指定値をずう〜っと、
その変数に対して使用しろというもので、変数の初期化の一つの手段です。
Dimension SelfRefer = {0};Self_Refer
とやります。頭のいいコンパイラーは、いったん(3)を無効と判断したものの、
初期化の値0が使おうと思っていた2バイト整数の0と一致してしまったので、
(3)も有効ではないかと疑い、迷った末に(3)も動作仕様書に含めてしまいました。
今回ばかりは頭の良いコンパイラーもだまされました。
3.「不正な処理です」
コンパイラーがエラーもバグも何一つ吐き出しません。
信じられないことにリンカーもあっさり通過し、
あろうことかEXEファイルまで出来ちゃってます。
今までさんざんエラーやバグに苦しんでいたプログラマーは、喜びいさんでEXEを起動します。
出力画面の描画領域には、
SelfRefer = {0}
SelfRefer = {0,{0}}
SelfRefer = {0,{0,{0}}}
SelfRefer = {0,{0,{0,{0}}}}
SelfRefer = {0,{0,{0,{0,{0}}}}}
SelfRefer = {0,{0,{0,{0,{0,{0}}}}}}
SelfRefer = {0,{0,{0,{0,{0,{0,{0}}}}}}}
SelfRefer = {0,{0,{0,{0,{0,{0,{0,{0}}}}}}}}
・
・
・
・
・
「このプログラムは不正な処理を行いました」
4.プログラミングと数学基礎論
しかしこのように考えてみると、プログラミングと集合論は、
形式的にほとんどパラレルな対応がつくにもかかわらず、その中身は正反対です。
一方では厳密に自己参照を拒否し、他方では自己参照的手法のオンパレードです
(超限帰納法や対角線論法)。数値計算の方にも、サブルーティンの再帰コールという
一見自己参照的な手法がありますが、これは効率上の問題からサブルーティンのコピーを繰り返し
メモリ上に生産するだけで、本当の自己参照ではありません。
それが本当の自己参照なら、コンパイラーがそのコードを蹴ります。
集合論を含む数学基礎論での自己参照性はもっと本質的で、
まさに人間は有限のリソースしか扱えないので、それしか無限を生成する手段がないからなのでは?
と思えます。数学基礎論によって計算理論の基礎ができ、コンピューターの普及が
今度は数学基礎論を支援していると、どっかで読んだ覚えがありますが、
それは両者をパラレルに対応づけることができ、対応づけられる根っこには、
人間が有限のリソースしか扱えないことがあるのでは?となんとなく想像します。
さっき言った以上に、あくまでもっとなんとなくですが。

| NO.1224 | 2002.6.5. | 水の流れ | 最長距離数 |
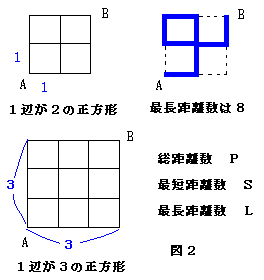
太郎さんは、よく「図1のような碁盤の目になった町で、
A地点からB地点への最短距離で行く道順の総数を求めよ。」と言う問題に出合います。
これは組み合わせの考え方で解くことができます。
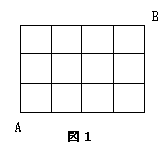
では、A地点からB地点へくねくねと遠回りをして行くと、最長距離数は幾つになるか。
また、道順の総距離数は幾つになるかを考えました。ただし、同じ道を1回しか通れないものとし、
小正方形の1辺の長さを1とする。
例えば、図2の1辺が2の正方形の場合は、総距離数Pは12,最短距離数Sは4、
最長距離数Lは8になります。
ここで、問題です。
問1.1辺が3の正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
問2.1辺が4の正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
問3.1辺が5の正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
問4.1辺がnの正方形の場合は、総距離数P,最短距離数S、最長距離数Lを求めよ。
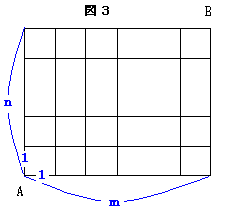
次に、長方形の碁盤の目を考え、1辺の長さがmとnの長方形を考えます。
問5.
(1)m、nがともに偶数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
(2)m、nがともに奇数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
(3)mが奇数、nが偶数のとき、総距離数P,最短距離数S、最長距離数Lを求めよ。
<問題の出典は、数研出版が出している数研通信NO24の中にあったものです。>

| NO.1225 | 2002.6.6. | prospero | Bezier曲線の問題 (6) |
かれこれ15年程前, この問題について考えたことがあります. といっても,
数学の問題としてに考えたのではなく, コンピュータプログラムでどう実
現するか, ということです. ですから, 証明もしていませんし, けっこう
いいかげんですが, 参考になるかと思いますので, 少し説明します.
当時, Adobe がその総力を結集して(?)世に送り出した PostScript を詳
しく調べれば分かるのですが, PostScript では Bezier 曲線を太らせた
曲線を作るために Bezier 曲線を細かな線分に分割し, それを太らせてい
ます.
なぜか?
PostScript では, Bezier 曲線を描画するのに, 本多様が示された, パラ
メータを使った式をそのまま用いるのでははく, 1 つの Bezier曲線を 2
つに分割する操作を, 分割された各部分が十分小さくなるまで繰り返すこ
とによって折れ線近似するという方法を取っています. 1 つの Bezier曲
線を 2 つに分割する操作は, 加減算と 2 で割るという作業だけでできま
すから, 当時の非力なコンピュータにとっては, この方法は極めて有効だっ
たわけです.
Bezier 曲線を太らせた曲線が高精度に Bezier 曲線で近似できる方法が
あれば, Bezier 曲線を細かな線分に分割してからそれを太らせる必要は
ありません. なぜなら, その方が塗り潰す領域を囲む線分の数が 1/3 ぐ
らいに減り, そうです!, 当時の非力なコンピュータにとっては一層有利
な方法であったはずだからです. しかし, Adobe の頭能を持ってしても線
分を太らせる方式を選ばざるを得なかった理由は, それができなかったか
らなのだと私は推測しています.
もし, 様々な PostScript をお使いになれる環境がおありでしたら, 以下
のプログラムを試してみて下さい. 多くの PostScript の実装で, 線分を
太らせる方式が用いられていることが確認できるはずです.
%!PS 0 0 moveto 72 0 0 72 72 72 curveto 10 setlinewidth strokepath 0 setlinewidth stroke showpage
なお, 線分を太らせる方式の場合, 凸の部分でも凹の部分でも太らせた端
の部分を隣の線分の太せた端の部分と繋ぐだけで良いので, アルゴリズム
は簡単です. ただし, 塗り潰す時に, non zero で fill するのは重要で
す. eo-fill すると線分の内側に塗り残しができます.

| NO.1226 | 2002.6.22. | 本多欣亮 | Bezier曲線の問題 (7) |
prosperoさん、興味深いお話と貴重なコードの提示ありがとうございまし
た。PostScriptのクローンインタプリタ(LEGATOSCRIPT)が使えるので、
参考にさせていただきます。

| NO.1227 | 2002.6.22. | 水の流れ | 1次リーグの勝点 |
太郎さんは、2002年ワールドカップのサッカー1次リーグの勝ち点について興味を持っています。
前後半90分の試合を行って、勝ったら勝ち点3点、引き分けたら勝ち点1点、
負けたら0点となっています。
ここで、問題です。
実はこの問題はNO.860 リーグ戦の勝ち点(第60回の応募問題)
と同じです。エレガントな解法を期待しています。
問題1:3チームでこの勝ち点方法でリーグ戦を行ったとき、
(1)1チームの勝ち点の取り方は、何点から何点まであって、
それらは何通りの試合から生まれるか。
(2)3チームの勝ち点の取り方をすべてあげてください。
問題2:4チームでこの勝ち点方法でリーグ戦を行ったとき、
(1)1チームの勝ち点の取り方は、何点から何点まであって、
それらは何通りの試合から生まれるか。
(2)4チームの勝ち点の取り方をすべてあげてください。
問題3:5チームでこの勝ち点方法でリーグ戦を行ったとき、
(1)1チームの勝ち点の取り方は、何点から何点まであって、
それらは何通りの試合から生まれるか。
(2)5チームの勝ち点の取り方をすべてあげてください。

 E-mail
E-mail
 戻る
戻る