
Weekend Mathematics/コロキウム室/NO.133
| NO.1135 | 2002.1.22. | シーラカンス | ユークリッド距離(1) |
ある分布から、もうひとつの分布までのユークリッド距離を求めて
くださいとあるのですが・・・・ わかったようでわからないので
どなたか概念を教えていただければ幸いです。

| NO.1136 | 2002.1.23. | 水の流れ | 交代級数の和・その2(2) |
さて、第91回の応募問題で、ヒントになる関数をお送りします。 この関数を微分して、工夫すれば答えに到達します。
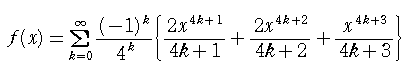
次に、NO.1133「月の光」さんがsin 20゜の値を求めては と ありました。
この値は スムーズにはいかないようです。的はずれかもしれませんが、
チャレンジしてみました。
20゜=θ として、60゜=3θ となり、3倍角の定理を利用します。
√3/2=sin 60゜=3X−4X3 (X=sin 20゜とおく)
8X3−6X+√3=0 を Mathematica で解くと、
以下のようになります。i あるのが気になります。
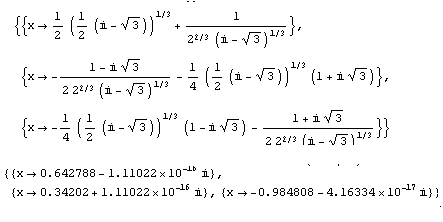
実際に、グラフをかけば 3つの実数解がありますから。変な気がします。
で、近似値を求めてみました。
3個の値がでてきますが、三角関数表から、判断するのに、
sin 20゜=0.34202
sin 40゜=0.642788
sin 260゜=-0.984808
となりました。あまり参考にはならないと思いますが、報告します。
さらに、ある方は sin 10゜の値を累乗根の形で求まらないかと尋ねておられます。
この方は、3゜から90゜までの3の倍数の角度で sin の値をすでに、
累乗根の形で求めておられます。

| NO.1137 | 2002.1.24. | T_Tatekawa | フラクタル図形(2) |
高校生の頃に類似の問題を考えた事があり,その時も悩みました.
AB+AC=2 が BC=1 に近付いていくという点ですが,確かに線分の
位置は近付いています.しかしこれを関数として書くと,
BC は直線 y=0 の一部分ですが,折り畳まれた線分は傾きが 0
でない二種類のものが混在した状況になります.
この折り畳みの操作を無限に繰り返していった場合,この折り
畳まれた関数は「連続だがほとんどいたるところで微分不可能」
となります.二つの線分の同一視はしてはいけないでしょう.
また,フラクタルとこの微分不可能な図形の関連が思い付きます.
フラクタル次元を求める際のいくつかの方法の一つに,「相似次元」
があります.これは,図形の一部分を切り取ってきて,それを
いくつか組み合わせます.すると切り取った一部分よりも大きい
図形の別の一部分に一致する場合があります.
この時に,組み合わせに使った部分の数 N と,二つの図形の相似比
n を使って,
D = log N/ log n
という形でフラクタル次元を定義します.
今の図形の場合,例えば AB の部分を取り出して二つ組み合わせると
AC の部分になります.AB と AC の相似比は 2 なので
D = log 2 / log 2 =1
となり,直線の次元と一致します.このような次元が整数の場合は
フラクタル図形とは呼びません.
例えばコッホ曲線ならば一部分を取り出して 4 つ集めると
相似比 3 の図形になります.
コッホ曲線
この場合は
D= log 4 / log 3 = 1.26
となり,フラクタル図形であるといえます.

| NO.1138 | 2002.1.24. | Junko | フラクタル図形(3) |
第27回 直角二等辺三角形の問題のまとめの項に
フラクタル図形についての話しがありますので、参考までに・・・。

| NO.1139 | 2002.1.24. | 水の流れ | ユークリッド距離(2) |
「新数学辞典」(大阪書籍)で調べてみると、
n次元空間の2点A,Bの距離を、下の図のように定義します。
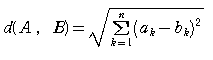
この距離をユークリッド距離という。
これは、今、高校で教えている、1次元、2次元、3次元の距離と同じ定義になります。

| NO.1140 | 2002.1.25. | hiro | ラプラス変換(1) |
ある本で読んだのですが、
ラプラス変換というのがいまいち分らないのですが教えて頂けませんでしょうか

| NO.1141 | 2002.1.25. | 水の流れ | ラプラス変換(2) |
ラプラス変換について、「新数学事典」(大阪書籍)
で調べたので、報告します。
区間[0,∞ )で定義された関数f(x)に対して
図1のように 定義されたF(s)をf(t)のラプラス変換という。
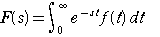
また、同じような積分変換に、よく知っているフーリエ変換があります。
ちなみに、区間(−∞,∞ )で定義された関数f(x)に対して
図2のように 定義されたF(u)をf(t)のフーリエ変換という。
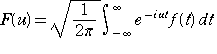

| NO.1142 | 2002.1.26. | こざっぱ | マイナスの数(1) |
数のお話ですが、最近、会社で話題になったのです。
マイナスの数の切り上げ、切り捨て、四捨五入。
たとえば、−5.50は切り上げ、切捨て、四捨五入して整数にする場合に
どうなるのでしょうか?意見が2つに分かれてしまいました。
私は、
切捨ては小数部を取り去るので −> −5
切り上げは小数部を切捨ての反対にする −> −6
四捨五入は??(わからない)
と思っております。真相はいかがなものでしょうか。
ヒントなどありましたら教えてください。

| NO.1143 | 2002.1.27. | Junko | マイナスの数(2) |
「マイナスの数の切り上げ、切り捨て、四捨五入」ですか・・・
これはまたおもしろいところに着目しましたね。
なかなかおもしろいと思います。
これは定義されているのかなあ?
私の知る限りでは、定義されていないようにも思います。
ご存知の方がいたらお知らせください。
真相はわかりませんが、
私なりに考えてみました。
私が思うには、「−5.50」の切り上げは「−5」、切捨ては「−6」、
四捨五入は「−5」です。
その心は? 数直線をイメージしてください。
自分を含んで自分より、右にある(大きい)最も近い整数を与える関数が「切り上げ」と、考えるわけです。
自分を含んで自分より、左にある(小さい)最も近い整数を与える関数が「切捨て」
(ガウス記号→NO.1127)
左右(大小)関わらず、自分に最も近い整数を与える関数が「四捨五入」
ただし、ちょうど真ん中の時は「切り上げ」
でも一方で、プラスマイナスの符号は単に方向だけを表している、
例えば黒字ならプラスで赤字ならマイナスというように・・・、と考えるならば、
絶対値で切り上げ、切り捨て、四捨五入した後にマイナスの符号を付け直すという定義も
考えられますね。
定義というのは、どういう風に決めるということですから、複数の定義があってもいいと
思いますが、どの定義が最も合理的かということになりますよね?
これでディベートしたらおもしろいかも?

| NO.1144 | 2002.1.28. | DDT | マイナスの数(3) |
「マイナスの数の切り上げ、切り捨て、四捨五入」が定義されているかどうかは、
私も知りませんが、慣用的には決まっているようです。
一例として、Visual Basicの切り捨て関数類を上げます。
Visual Basicは、DOS上の汎用(?)言語だったN88BasicやQuick Basicの後を継いで、
今ではWindowsプログラムの最も標準的言語です(ちょっと言いすぎですね)。
またDOS上の代表的数値計算高級(?)言語であったFORTRANも、
Visual Basicの切り捨て関数系と同じ構成を持ち、Visual Fortranとなって、
Windowsプログラムの一部の世界では未だに健在です。
Visual Basicの切り捨て関数系(型変換関数が正式名称です)
| Int(x): | IntはInteger(整数)の略です。機能は、負の整数に対してもガウス記号と同じです。 Int(-5.5)=-6。 |
| Fix(x): | 正負に関係ない本当の小数部切り捨てです。Fix(-5.5)=-5。 Fixは固定の意味で、小数桁数を0桁に固定の意味と思います。 |
| CInt(x): | Casting to Integerの略かと思われます。 Castの直訳は、配役=役者を別の人格である役どころに当てはめるの意味ですが、 それを、浮動小数点を持つ実数型などをFixな整数型に強制変換する意味に流用しています。 語源は、C言語の強制型キャストに由来するようです。機能は正負対称な四捨五入です。 Int(-5.5)=-6。 |
結局、切り捨て,切り上げに関しては、正負非対称な方法も対称な方法も、
場合によって使い分ける形で流通しているようです。
四捨五入に関しては、正負対称なほうが数値計算上は楽です。
あとExcelのWorkSheet関数に、RoundDown,RoundUp,Round関数があります。
これらの機能も調べてみると面白いかもしれません。

 E-mail
E-mail
 戻る
戻る