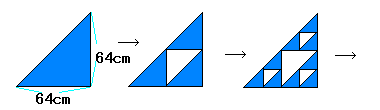
Weekend Mathematics／問題／問題27

２７．直角二等辺三角形の問題


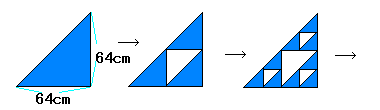
上の図のように、直角二等辺三角形から順々に辺の長さが半分の大きさ の直角二等辺三角形を取り除いていく操作を繰り返していくとき、 次の問いに答えなさい。

（１）２回目、３回目の操作の後の青い部分の面積を求めなさい。

（２）５回目の操作の後の、青い部分の面積を求めなさい。

（３）青い直角二等辺三角形が６５６１個できるのは、 何回目の操作ののちですか。




問題の出典


パズルより面白い中学入試の算数

ピ−タ−・フランクル

講談社

調布中学校'93






答えと解説












答えと解説

解答・その１

（ペンネ−ム：かに）

問題の操作を繰り返すとき、辺の長さと青い部分の直角二等辺三角形は それぞれ1/2倍、3倍ずつ増えるので

  1. ２回目では　1152 cu、　３回目では 864 cu
  2. 486 cu
  3. ８回目




解答・その２

（ペンネ−ム：２丁目の山田）

一般にｎ回の操作後、 三辺の長さが64/2n,64/2n, 64/2n×√2の直角二等辺三角形が3n個できるから、
ｎ回目の操作後の青い部分の面積 Ｓn＝3n×(1/2)×(64/2n)2＝2048×(3/4)n とかけるので、

  1. ２回目：Ｓ2＝2048×(9/16)=1152
    ３回目：Ｓ3＝864
  2. ５回目：Ｓ5＝486
  3. 6561=38より　８回後の操作の後




解答・その３

（ペンネ−ム：Ikawa Bird）

１２．操作を一回するごとに、青い部分の面積は３／４倍される。
n回目の面積をAnとすると
A0=64×64/2=2048, An+1=An×(3/4)が成り立つ。
よってAn=2048×(3/4)nより
A2=1152, A3=864, A5=486となる。 （単位はすべてcm2）
ちなみに、２７回繰り返せば面積は１を切ります。

３．一回操作するごとに三角形の個数は３倍される。
n回目での個数をBnとすると、Bn=3n。
n=logBnより、log6561=8。
よって８回目の操作の時。（底は3です）




解答・その４

（ペンネ−ム：ふー）


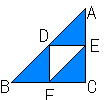
先ず(1)(2)の問題を解くために、青い部分の面積Ｓｎ ｛ｎ：操作回数｝を求める一般式を立ててみる。

ｎ＝１の場合を考えてみると、
問題から、△ＡＢＣと△ＤＥＦの相似比＝１：２ になるので、 △ＡＢＣと△ＤＥＦの面積比＝１２：２２＝１：４
従って、△ＤＥＦの面積＝(△ＡＢＣの面積)×(1/4)であるから、
Ｓ１＝(△ＡＢＣの面積)×(3/4)

同様にｎ＝２の場合は、 

Ｓ２＝△ＡＤＥ×(3/4)＋△ＤＢＦ×(3/4)＋△ＥＦＣ×(3/4)
　　＝Ｓ１×(3/4)
　　＝△ＡＢＣ×(3/4)２

ｎ＝３以降も同様に考えられることから、 青い部分から直角二等辺三角形を取り除く操作は青い部分の面積を３／４にすることと同意である。 よって、最初の図形の面積が２０４８cm２であるから青い部分の面積Ｓｎは、 次の一般式で表せる。
Ｓｎ＝２０４８×(3/4)ｎ

つまり、
(１)の答え　　２回目の操作の後の面積は １１５２ cm２
３回目の操作の後の面積は 　８６４ cm２
(２)の答え　　５回目の操作の後の面積は 　４８６ cm２
(３)は、１回の操作で直角二等辺三角形がそれぞれ３つに分割されるので、 直角二等辺三角形の個数＝３ｎ{ｎ：操作回数}になる。
よって、６５６１を素因数分解すると ６５６１＝３８ であるから、
答は　８回の操作の後




解答・その５

（ペンネ−ム：マサボー）








解答・その６

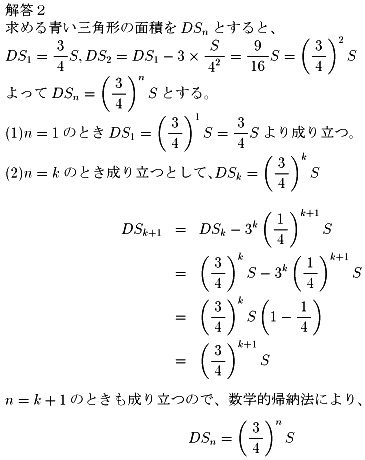
（浜田　明巳 ）

  1. ２回目１１５２平方センチ，３回目８６４平方センチ
  2. ４８６平方センチ
  3. ８回目

次のＵＢＡＳＩＣのプログラムによって求めました．
１回の操作で辺の長さが半分になり， 青い直角二等辺三角形の個数が３倍になることが分かります．
三角形の個数が６５６１個になるまで計算を続け， 最後に答を表示するようにします． 

10   'asave "MONDAI27.UB"
20   dim 答(4):回数=0:個数=1:辺=64
30   while 個数<>6561:回数+=1:辺*=0.5:個数*=3
40    if or{回数=2,回数=3,回数=5} then 答((回数<4)*(回数-1)+(回数=5)*3)=fn面積(個数,辺)
50   wend:答(4)=回数
60   for J=1 to 4:print "答(";right(str(J),1);")=";答(J):next:end
70   fn面積(個数,辺):面積=個数*0.5*辺*辺
80   if int(面積)=面積 then 面積=int(面積)
90   return(面積)
ちなみにＵＢＡＳＩＣのソフトは現在インターネットから ダウンロードできます． このＵＢＡＳＩＣの特徴は計算のスピードが速く， 桁数も多く扱えることができ，また漢字を名前に使えることです　



正解者

かに

浜田　明巳

２丁目の山田

Ikawa Bird

マサボー

ふー

燃えるサラリーマン




まとめ

今回の問題はフラクタル図形の例として有名な 「シェルピンスキ−のガスケット」です。
これは問題(は直角二等辺三角形でしたが)にあるように、 正三角形をさらに４つの合同な正三角形に分け、 中央を取り除いていくという操作を無限に繰り返すことで得られる図形です。

フラクタル(Fractal)図形というのは、 一言で言えば、「自己相似」
どのような小さな部分を見ても、全体と相似という性質をもっているのです。

さて問題を再確認してみます。



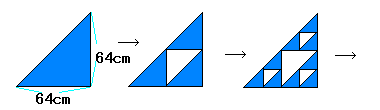
これらの極限を(つまり無限回の操作をしたと)考えてみると、 面積０の三角形が(無限大)個あり、全体としての面積は０、 辺の長さは(無限大)ということになります。
この図形は、面積０ですから２次元の図形とは言えません。 しかしながら辺の長さは無限大ですから、１次元というのも無理があるように思います。
そこで、１次元と２次元の間にある非整数の次元という概念を考えた人がいるのです。

マンデンブロ(1924〜)という人がフラクタル次元というものを定義しました。
精度をｒ倍したときに、長さがＮ／ｒ倍になったとすると、
フラクタル次元＝(logＮ/logｒ)とします。
(全体を(1/r)に縮小した相似形Ｎ個から成り立つと考えてもいい。)

この定義に従えば、精度を２倍にしたときに長さが(3/2)となっています (1/2に縮小した相似形３個から成り立っています)から、 「シェルピンスキ−のガスケット」のフラクタル次元は、
log3/log2=1.584962501･･･　となります。
これはフラクタル図形の複雑さの度合いと解釈することもできます。


さて、「Mathematicaで絵を描こう」（中村健蔵著、東京電機大学出版局、\3500)という本の中に シェルピンスキ−のガスケットの綺麗なグラフィックスがありましたので、 著者ご本人の承諾を得てプログレットと共にここに紹介します。



プログレット(左上の図) 

a = N[Sqrt[3]/2];
b=Polygon[{{0,0},{1,0},{.5,a}}];
SetAttributes[fen,Listable]
fen[Polygon[{a_, b_, c_}]] := {Polygon[{a, (a + b)/2, (a + c)/2}], 
                               Polygon[{b, (a + b)/2, (b + c)/2}], 
                               Polygon[{c, (c + b)/2, (a + c)/2}]}
p = Table[{Hue[i/6. ], Nest[fen, b, i]}, {i, 0, 5}];
  Show[Graphics[p], AspectRatio -> Automatic]
プログレット(右上の図、下２行を差し替え) 
p=Nest[fen,b,7];
Show[Graphics[p],AspectRatio -> Automatic]


四角形のギャスケット

正方形から、正方形を取り除いていくことで作られています。

フラクタル次元は、 log8/log3=1.892789261･･･　
三角形のガスケットの真似をして、色をつけずに表示してみました。 繰り返しを５回にしています。 先程の三角形のガスケットよりも若干次元があがっているのが、 図から感じとれますか？



シェルピンスキ−のスポンジ(n=3)

立方体から立方体を取り除いていきます。
フラクタル次元は、 log20/log3=2.726833028･･･　

著者､中村健蔵さんのWebページでは、 フラクタル図形はもちろん、「mathematica」でかかれた素晴らしい画像をたくさんみることができます。

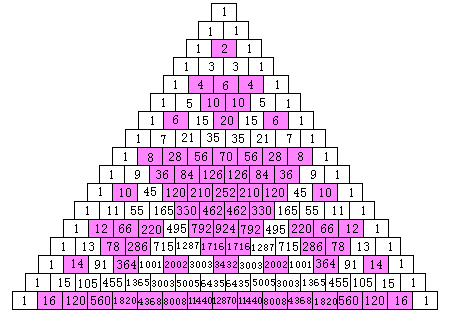
コロキウム室のNO.224で扱った パスカルの三角形です。 偶数の所だけ色がつけてあります。
Sierpinskiのガスケットは、だんだんと細かくしていきますが、 こちらはだんだん大きくなっていくところがおもしろいですね。

さて、もう１つフラクタル図形を紹介しましょう。 「コッホ曲線」と呼ばれるものです。

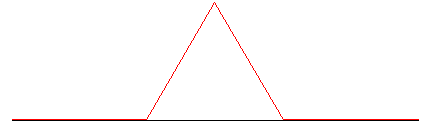スウェ−デンの数学者、ヘルジ・フォン・コッホ(1870〜1924)に発見されたことからこの名で呼ばれます。
長さ１の線分からスタ−トします。 まずこれを３等分します。 真ん中の1/3の部分を、それを１辺とする正三角形の他の２辺で置き換える。

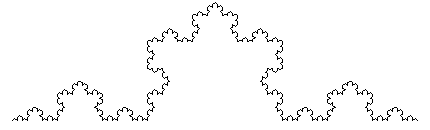以下、この操作を直線部分に対して無限に繰り返します。 ただし置き換えをする時には、どちら側に置き換えるかを一定にしておきます。
左図は、前述「Mathematicaで絵を描こう」の中にある図をお借りしています。

コッホ曲線はもちろん連続ですが、極限状態では直線部分が存在せず、 いたるところ折れ線だらけ、つまりいたるところ微分不可能ということになります。
精度を３倍にすると、測定値は4/3になるので、 フラクタル次元は、log4/log3=1.261859507･･･　となります。

さて最後に「Encyclopedia」からの引用です。
フラクタル幾何学は、たんなる数学的な抽象ではない。 海岸線は、雪片と同じように、細かくはかるにつれてかぎりなくその長さが長くなる。 マンデルブロによれば、山や雲や銀河や星団、 その他さまざまの自然の形や現象がよく似た性質をもっており、 フラクタル幾何学の自然科学における応用は急速にひろがっている。 さらにフラクタルがうつくしい図形としてしめされることから、 コンピューター・グラフィックスでも重要なものとされている。 フラクタルはまた、コンピューターで静止画や動画の情報を圧縮するのにもちいられる。 1987年、イギリスの数学者マイケル・バーンスリーは、 フラクタル変換という方法をみいだした。 この発見によって、自然をうつしとった画像(デジタル化された写真)の中で フラクタルになった部分をみつけて、その画像を生みだす情報、 つまりフラクタル・コードを自動的に検出し、 画像情報を圧縮する方法が可能になった。 このフラクタル画像圧縮方式は、マルチメディアをはじめ、 画像を基本としたコンピューターのさまざまな情報処理ソフトに活用されている。
Microsoft(R) Encarta(R) 97 Encyclopedia. (Ｃ) 1993-1997 Microsoft Corporation. All rights reserved.



戻る