
Weekend Mathematics/コロキウム室/NO.130
| NO.1107 | 2001.12.1. | yokodon | 動く楕円(3) |
NO.1097の BossF さんのお答えで、正解です。
これでメデタシメデタシ・・・としたいところですが、おまけの考察で屋上屋を重
ねさせて下さい。
確かに、代数的には、拘束条件の同値変形により、中心が(q, 0)で半長軸 2(y
軸方向)、半短軸 1(x 軸方向)の楕円が得られて、-1 ≦ q ≦ 1 のもとでその楕
円の掃過する領域を求めれば答えなのですが、幾何的にはどの様な状況になっている
か(言い換えると、点P、点Qの位置関係から点Rの動く範囲が、q を固定する毎に
楕円として定まるのは…あくまで幾何的に見て…どうしてなのか?)というのを、改
めて問題にしてみたいと思います。

| NO.1108 | 2001.12.1. | yokodon | ある不等式の証明(1) |
(1)a,b を a < b なる実数とし、f(x), g(x) を [a,b] 上で可積分な関数とする。
次の不等式が成り立つことを示せ。
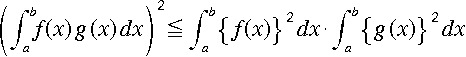
(2)0 < x < π/2 に対して、次の不等式が成り立つことを(1)の結果を用いて
示せ。
sin(x) > 2/π・x
#問(2)は、「グラフを書く」「(左辺)-(右辺)なる関数を微分する」のではな
い方法でやってみて下さい。

| NO.1109 | 2001.12.4. | 水の流れ | 複素数の平方根(1) |
今、太郎さんは学校で生徒に複素数平面を教えています。
平方根の性質を拡張して次のことが成り立ちます。
(1)a、bがa>0、b<0のとき、
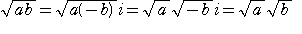
が成立する。
(2)a>0のとき、
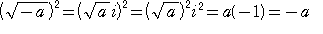
が成立する。
(3)z2=a2の解は、z=±a である。
また、複素数zをa+biで表して、a、bがともの整数のとき、
zを複素整数という。ここで、問題です。(もちろん、iは虚数単位を表している。)
問題1:z2=48+14i のとき、複素数zを求めよ。
問題2:上の問題を2重根号のはずし方を利用して、解いてください。
問題3:z2=a+biのとき、複素数zをa、bで表してください。
(ただし、a、bは実数とする)
問題4:z2=a+biで、b=2002のとき、複素整数zを求めてください。

| NO.1110 | 2001.12.17. | BossF | 複素数の平方根(2) |
問題1[解]
z=x+yi (x,y∈R)とおくと、
z2=(x2-y2)+2xyi
∴ x2-y2=48…① xy=7…②
②より、y=7/x これを①に代入して分母を払い、整理すると
x4-48x2-49=0
x∈Rだから
| x2 | =24+√(242+49) |
| =24+√625 | |
| =49 |
問題1[解その2]
z=r (cosθ+i sinθ) (r>0) とおきます。
48+14i=50(24/25+(7/25)i)だから
cosα=(24/25), sinα(7/25) なる第1象限の角αを用いて
z2=r2(cos2θ+i sin2θ)=50(cosα+i sinα)
∴ r2=50, 2θ=α+2nπ i.e. r =5√2 ,θ=(α/2)+π
ここで、(cos(α/2))2=(1+cosα)/2=49/50
i.e. cos(α/2)=7/(5√2) sin(α/2)=1/(5√2)
よって、
| z= | ±5√2(7/(5√2)+i/(5√2)) |
| =±(7+i) …答 |
題2[解]
48+14i=(49-1)+2x7x1xi=(7+i)2
i.e. z2=(7+i)2
∴ z=±(7+i) (∵(3)) …答
問題3[解]
まず、b=0 のとき、z=±√a
つぎに、b≠0 のとき
z=x+yi (x,y∈R)とおくと、
z2=(x2-y2)+2xyi
∴ x2-y2=a…① 2xy=b…②
ここで、b≠0 よりy≠0 だから
②より、y=b/(2x) …②’
これを①に代入して分母を払い、整理すると
x4-ax2-b2/4=0
x∈Rだから
x2={a+√(a2+b2)}/2
i.e. x=±√{a+√(a2+b2)}/√2
これを②’に代入整理して
y=±b/lbl・√{√(a2+b2)-a}/√2
∴z=±1/√2・[√{a+√(a2+b2)}+i b/lbl・√{√(a2+b2)-a}]…答
問題4[解]
z=p+qi とすると z2=p2-q2+2pqiだから
2pq=2002 i.e.pq=1001 なる整数p,qを見つければ好い
ところで、1001=7x11x13 したがって
(p,q)=(±7,±143),(±143,±7),(±13,±77),(±77,±13),(±11,±91),
(±91,±11) 、(±1001,±1),(±1,±1001) (複号同順)よって
z=±(7+143i),±(143+7i),±(13+77i),±(77+13i),±(11+91i),
±(91+11i),±(1001+i),±(1+1001i) …答

| NO.1111 | 2001.12.20. | DDT | ある不等式の証明(2) |
(1) 詳しい証明はできませんが、
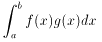
を関数空間上のユークリッド内積と考えれば、
内積公式
u・v≦|u|・|v|
より明らか。
ここで「・」は内積を表し、u,vは任意のベクトル、||はノルムを表す。
(2) 0 < x < π/2で、sin(x)と2/π・xは単調増加かつ、x=0でsin x=2/π・x=0なので、
2/π・x < sin x
より、
2/π・x sin x < sin2x
が成り立てば良く、任意の0 < x < π/2で、
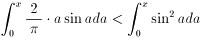
であれば良い。ここで(1)より、
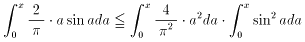
が成り立つが、
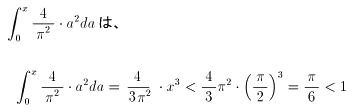
なので、
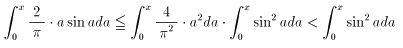
となり、OK!。

| NO.1112 | 2001.12.20. | 水の流れ | 奇数の積の和(1) |
今、ここに、整式 f(x)=(1-x)(1-3x)(1-5x)・・・{1-(2n―1)x}
がある。ここで、問題です。
問題1:この 整式 f(x)を展開したとき、x の係数を求めよ。
問題2:この 整式 f(x)を展開したとき、x2の係数を求めよ。
問題3:
n個の奇数1,3,5,・・・,2n―1から重複せずにr個取って作った積を、
r個の選び方すべてにわたって加えたものを
Prとするとき、
P1+P2+P3+・・・+Pnを求めよ。

| NO.1113 | 2001.12.21. | DDT | 勝負の行方・その後 |
先月の問題59 勝負の行方は、
後手必勝,先手必敗のゲームでした。
まさか先手必敗までついてくるとは、思いもしませんでした。
以下は、そういう状況のもとで考えたことだとご理解下さい。
最初この問題でも、二分木検索をやろうかと思わず考えました。
最近多分木検索プログラムに成功したので、やりたくてうずうずしてたわけです。
ゲームのプレイ回数は9回で、先手と後手で1と2の枝をつくるので、
場合分けの数は(29)2=262144程度で、最近のパソコンは無茶苦茶高速だから、
これくらい屁でもない!(30万円出せば、1.5GHz,512MB,20GBが手に入る時代ですから)。
でも止めました。
まず、262144通り全ての検索に成功したとして、
先手か後手が全て勝つような結論にはならないはずだ(実はなるんですね)。
先手必勝か後手必勝になるだろうという答えは、あらかじめ予想できました。
4対1くらいの比率で先手か後手有利という検索結果になるだろう。これでは*手必勝にならない。
では例えば、後手が勝つような二分木経路が存在することを示せば良いのか?。
しかしこれでは、後手に勝ち経路があるなら、同様に先手にも勝ち経路が存在するから、
*手必勝にならない。というか、これは先手か後手が全て勝つような検索結果にはならないこと
の同語反復だ(なるのですね)。
ではこの問題の要はなんだろう?。
「後手は数字2を常に2個づつ消去できる」=「後手はゲームをコントロールできる」
ことだと思いました。ここで「ゲームをコントロールする」とは、
一般に多分木選択となるゲームの各段階で、自分の勝経路を多分木分かれ道において
常に選択できることです。このような人をゲームマスターと呼びます(カッコつけて)。
ゲームの定義(またカッコつけます)
ゲームマスターの定義
ゲームステージの多分木選択において、対戦プレーヤーの選択に関わらず、
自分の勝ちにつながるプレイ(勝経路)が常に存在するプレーヤーのことをゲームマスターと呼ぶ。
もちろん間違った選択をして、ミスって負ける場合もある。
このように定義すると問題59 勝負の行方には、
次の一般的定理?の結論として別解が存在することになります。
ゲームに関する一般的定理?
ルールがゲームマスターの存在を許せば、ゲームマスターには必勝法が存在する。
[証明!?!?]
定義より明らか。
問題59 勝負の行方は、
後手がゲームマスターで全ての二分木選択が全て勝ち経路という例になります。
しかしこう考えると、ゲームマスターの存在を許すゲームはそもそも不公平です。
対戦者がどんなに頑張っても、ゲームマスターには常に勝つ手段が残るわけですから。
つまり対戦者に詰めの一手は存在せず、できることはゲームマスターのミスを待つのみで、
勝負の決するゲームも終盤に近づけば、双方とも煮詰まってくるので、
ミスはどんどん減って行くと思われます。このあたり将棋や囲碁,
チェスなんかはどうなっているでしょう?。
誰かゲームマスターの存在しないことを、証明してないんでしょうか?

| NO.1114 | 2001.12.24. | yokodon | 奇数の積の和(2) |
やってみました。計算違いがあったら、ゴメンナサイ。
f(x) の定義から、直ちに以下が言えますね。
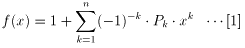
但し、Pk は、問(3)で定義される和積です。
(1)P1 を求めればいいことになります。
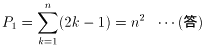
一部修正(12/26)
(2)P2 を求めればいいことになります。まず、
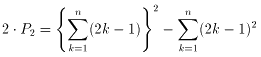
です。この左辺を計算して、
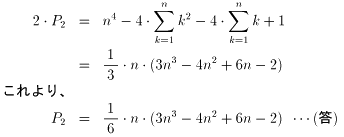
(3)[1] 式に、x = -1 を代入して、
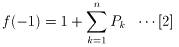
他方、
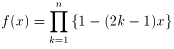
であるから、
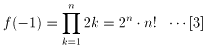
よって、[2] [3] の両式より、以下を得ます。
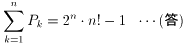
蛇足ながら、(3)を応用して、様々な和を用いて Pk を求めることが出来そうで
すね
(例えば、つまらない例ですが、(3)の結果を Sn として、
Pn = Sn -Sn-1 。
また、[1] 式に x = 1 を代入すると Pk の交代和が求まり、値は -1
となるので、k が偶数の場合の和と奇数の場合の P_k の和を求めることが出来る。
などなど)。
ってことは、題意の f(x) は、一種の母関数なわけでしょうか(尤も、
原理的には、0 でない n 個の異なる整数を f(x) に代入して出来る、Pk に関する
連立一次方程式を解けば求まるとは言え。でも、もっと上手い方法がありそうな気が
します)。
バイト先(;予備校です)で、「1~n の中から r 個(r ≧ 3)を取る積の総和を
求めたいが?」という質問をされて答えそびれたことがあるのですが、『今度同じ質
問をされたら使おう!』と思いました。(^^;
今度、暇なときに、
g(x) = Π(1 - kx )
や
h(x) = Π(1 - 2kx )
の場合について考えてみようかと思います。

| NO.1115 | 2001.12.28. | yokodon | ある不等式の証明(3) |
No.1108 の各不等式の証明(として、用意させていただいていたもの)を、
一応お送りしたいと思います。
(1)
f(x) ≡ 0 の時は、明らかに等号成立ですね。以下、それ以外の場合を考えます。
h(x) = (t・f(x) + g(x))2 の a → b での積分を考えます。
h(x) ≧ 0 ですから、積分の符号も“≧0”。
よって、積分結果を t の2次式と見ると、“2次式”= 0 という2次方程式の判
別式を D として、D ≦ 0 が成り立ちますね。
これから、目的の不等式を得ます。
(2)
超略解で失礼致しますが、(1)で
a → π/2 - x
b → 0
f(t) → 1
g(t) → {1 +(π/2)・ sin(t)}1/2
((1)の結果の積分変数を、予め t に書き換えておく)
とすると、実は直接示すことが出来ます。

 E-mail
E-mail
 戻る
戻る