
Weekend Mathematics/コロキウム室/NO.129
| NO.1099 | 2001.11.19. | Junko | 連続の証明(12) |
「f(x)<1/n はなぜいえるのでしょうか?」
逆に言うと、f(x)>=1/nになるようなxをすべて排除したからです。
無理数aの前後には、無限に有理数存在します。
つまりf(x)=0とならないxが無限に存在します。
しかしながら与えられたεに対して、f(x)<1/n<εとすることはできます。
それは適当なδ、(a-δ,a+δ)の中からf(x)>=1/nとなるxをすべて排除すればいいのです。
それは高々有限個ですから、δを小さくとることで可能なのです。

| NO.1100 | 2001.11.19. | truth | 三角形可能な確率(5) |
水の流れさんの解答は、
「折る点を2か所同時に(simultaneously)ランダムに選ぶ場合」
(NO.450や下記の問題と同じ)ではないでしょうか?
それとも「棒を折ってできた二本のうち長い方を選んで二本に折る」という条件は確率に影響しないのでしょうか?
問12(先日投稿した問題とは別のものです。NO.450
と同じです。原文をそのままうつしました。)
Take a stick of unit length and break it into three pieces. Choosing
the break point at random. (The break points are assumued to be chosen
simultaneously.) What is the probability that the three pieces can be
used to form a triangle?
HINT: The sum of the lengths of any two pieces must exseed the length of
the third. so each piece must have length < 1=2.
(直訳です。)
長さ1の棒を3本に折る。折る箇所はランダムに選び、またその二点は同時に選
ばれると想定する。このときできた三本で三角形が作れる確率を求めよ。(ヒン
ト:三本のうちどの二本の長さの和も、残りの一本の長さより大きくなければな
らない。つまりそれぞれの長さは1/2より小さくなければならない。)

| NO.1101 | 2001.11.19. | Junko | 三角形可能な確率(6) |
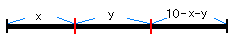
棒の長さを10とします。
最初に折った際に、短い方の棒の長さをxとします。0<x<5
次に折った棒を、y,10−x−yとします。0<y<10−x
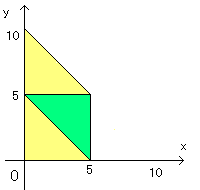
三角形ができるための条件は任意の2辺の長さの和が、
もう1辺の長さより長いことです。従って、以下の3条件となります。

| NO.1102 | 2001.11.20. | BossF | 三角形可能な確率(7) |
一部修正(11/21 19:00)
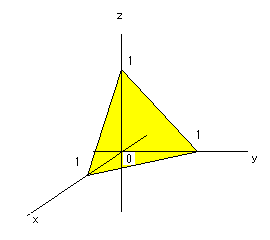
[NO.450の解]
領域S;x+y+z=1 (x,y,zは正数)
を図示すると右図(fig1)のような、正三角形Sになります。
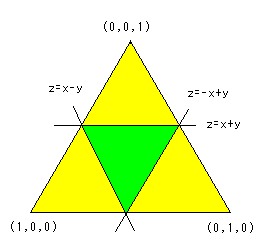
S上で三角不等式
lx-yl≦z≦x+yを考えたのが右図(fig2)
したがって、1/4…答
[No1092の解]
 最初におった長い方を再びおるというのは
x+y+z=1 (x,y,zは正数)かつ z≦x+y なるz=pが与えられたということですから、
このとき、三角形ができる確率dP(p)は
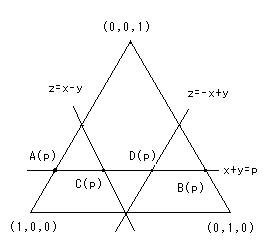
右図(fig3)より
最初におった長い方を再びおるというのは
x+y+z=1 (x,y,zは正数)かつ z≦x+y なるz=pが与えられたということですから、
このとき、三角形ができる確率dP(p)は
右図(fig3)より
dP(p)=C(p)D(p)/A(p)B(p)
ここで
C(p)D(p)=(√2)/2x{p/(1/2)}=(√2)p
A(p)B(p)=(√2)x{(1-p)/1}=(√2)(1-p)
よって
dP=p/(1-p)
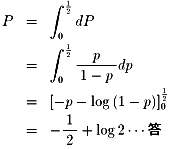
あまり自信ありません

| NO.1103 | 2001.11.20. | 匿名 | 三角形可能な確率(8) |
対数が出て欲しいのなら、解答は多分不適切なものです。
解き方としては、
規格化のために棒の長さは1とした方が確率の問題では無難です。
それで、最初に折った時の棒の長さをxとします。
(対称性から0.5までにして2倍できます。)
0〜0.5について三角形が成立するのは、
(1ーx)部分(長い方)のうち真ん中の部分で折る場合で、その幅はxになり
ます。
したがって、0〜0.5の範囲で、
関数f(x)=x/(1−x)を積分してやれば良く、
答えはそれを2倍するので、
2log2ー1(約0.38?)になると思います。

| NO.1104 | 2001.11.24. | 浜田 明巳 | 三角形可能な確率(9) |
エクセルで解いてみました(Macro1).
長さ1の線分内に,乱数により,2ヵ所の点を打つ。
それによって3つの線分に分け,その3つの長さをx,y,z
(x+y+z=1,0≦x<1,0≦y<1,0<z≦1)とする.
三角不等式
|x−y|<z<x+y
を満たすとき,三角形をなす.
この試行を1000000回繰り返し,確率を求める.
このマクロにより,確率は
0.250206≒1/4
となることが分かる.
どう見てもlog2が出て来るようには見えないのですが.
このマクロMacro1では,何のしがらみもなく2点を打ち,
3本の線分に分けるようになっています.
それに対して,Macro2では,最初に1点をとって1つの線分を取り出し,
残りの線分内にもう1点をとって,合計3本に分けるようになっています.
これは問題の条件には合っていないと思います.
とりあえず走らせてみると,確率は
0.193202≒log2−1/2
となり,ここでlog2が出るようです.
Option Explicit
Const N As Long = 1000000
Sub Macro1()
Dim A As Double, B As Double
Dim x As Double, y As Double, z As Double
Randomize Timer
Cells(1, 1).Value = 0
Cells(1, 2).Value = 0
Cells(1, 3).Value = "=A1/B1"
While Cells(1, 2).Value < N
A = Rnd: B = Rnd
x = Application.Min(A, B)
y = Abs(A - B)
z = 1 - x - y
'Cells(2, 1).Value = x: Cells(2, 2).Value = y: Cells(2, 3).Value = z
If Abs(x - y) < z And z < x + y Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
' Cells(2, 4).Value = "○"
'Else
' Cells(2, 4).Value = "×"
End If
Cells(1, 2).Value = Cells(1, 2).Value + 1
Wend
End Sub
Sub Macro2()
Dim x As Double, y As Double, z As Double
Randomize Timer
Cells(1, 1).Value = 0
Cells(1, 2).Value = 0
Cells(1, 3).Value = "=A1/B1"
While Cells(1, 2).Value < N
x = Rnd: y = Rnd * (1 - x)
z = 1 - x - y
'Cells(2, 1).Value = x: Cells(2, 2).Value = y: Cells(2, 3).Value = z
If Abs(x - y) < z And z < x + y Then
Cells(1, 1).Value = Cells(1, 1).Value + 1
' Cells(2, 4).Value = "○"
'Else
' Cells(2, 4).Value = "×"
End If
Cells(1, 2).Value = Cells(1, 2).Value + 1
Wend
End Sub

| NO.1105 | 2001.11.27. | Wolf | 分数の線 |
分数の真中にあるあの「線」って、何て呼べばいいんでしょうか?
どうでもいいことですが、気になるので、もしご存知でしたら教えてください。
1 / 2
↑
これ

 E-mail
E-mail
 戻る
戻る