コロキウム室

(一部訂正　11/1　15:00)

NO.873の３６の正の約数で３６と互いに素な整数の個数について，次のように考えてみました。
３６＝２^２×３^２（＝４×９）ですから， ３６以下の正の整数を４で割った余りおよび９で割った余りによって表に書いてみます。

		９で割った余り
		0	1	2	3	4	5	6	7	8
４でわった余り	0	0	28	20	12	4	32	24	16	8
	1	9	1	29	21	13	5	33	25	17
	2	18	10	2	30	22	14	6	34	26
	3	27	19	11	3	31	23	15	7	35

この表は，縦横の枠を作り，中へ１から順に数字を入れていくと規則正しく入りますので， すぐ完成します。また，３６の代わりに０を記入しました。
３６と互いに素となる数は，黄色の部分に表れます。
これは，（４−４/２）×（９−９／３）＝２×６＝１２と計算できますが
（４−４/２）×（９−９／３）＝３６(１−１/２)（１−１／３）です。
『数学読本６』（松坂和夫著，岩波書店）の1256ページおよび1342ページを参考にいたしました。

1. a=b のとき、a²+b²=2a²　　　 ab=a²であるから
   a²+b²=2ab　　すなわち　　a²+b²はabでわりきれる。
   
   
2. 「a²+b²はabでわりきれる。　→　a=b」の対偶を示す。
   すなわち「a≠b　→　a²+b²はabでわりきれない。」･･･(*)を示す。
   a≠bのとき、b=a+k　(k∈Ｎ)としてよく、
   a²+b²=a²+(a+K)²=2a²+2ak+k² =2a(a+k)+k²であるから
   (*)を示すには、k²がa(a+k)で割り切れないことを示せばよい。
   これを背理法によって証明する。
   k²=na(a+k)を満たす自然数nの存在を仮定すると、
   k²ｰnak-na²=0

   
   
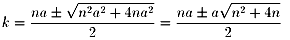
   k,nはともに自然数であるので、

   
   
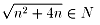
   従って、n²+4n=l²(l∈Ｎ)と書ける。
   n²+4nｰl²=0から

   
   
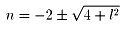
   いま、n∈Ｎであるから

   
   
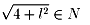
   従って、4+l²+m²(m∈Ｎ)と書ける。
   このとき、4=(m+l)(m-l)
   (m+l)＞(m-l)で、(m+l)∈Ｎ、(m-l)∈Ｚであるから、
   {(m+l),(m-l)}={4,1}
   これを解くと、m=5/2,l=3/2で、m∈Ｎ、l∈Ｎを満たさず、不適当である。
   よって仮定は誤りであり、k²がa(a+k)で割り切れない

コロキウム室NO.34　オイラーの多面体の定理について質問があります。
「多面体の面が全て三角形分割されているとき（三角形の数）−(辺の数）＋（頂点の数）＝2」
というのは分かりましたが、この後どうやって
「多面体において（面の数）−(辺の数)＋（頂点の数）＝2」というのを示せばよいのでしょうか。
僕は、これは「ｎ角形の内角の和は180（ｎ−2）度」の証明と関係があるな、 と思ったのですが残念ながらこの定理も自分では証明することができませんでした。

多面体の各面が三角形分割されていなかったとしたら、NO.34　オイラーの多面体の定理 で平面を三角形分割したのと同じようにすればできると思います。 つまり何本かの辺を加えることで、三角形分割にすることができます。 その際、加えた辺の数とそれによって増えた面の数が同じなので、オイラ−数はかわりません。

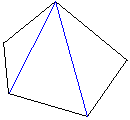「ｎ角形の内角の和は180（ｎ−2）度」ですが、 ｎ角形のある１点から、自分と両隣り以外の(ｎ−３)ヶ所の頂点にむけて、 対角線をひくことで(ｎ−２)個の三角形に分割できます。 三角形の内角の和は１８０度ですから、ｎ角形の内角の和は180（ｎ−2）度となります。 しかしこれは、凸ｎ角形の場合です。

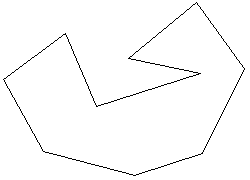凸ｎ角形でない場合を考えます。
左のような１０角形を例に考えてみます。

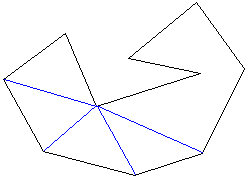頂点を１つ選んで端から三角形分割をしていきます。
必要に応じて、対角線をひく頂点を変えますが、その際引いた対角線の数がｍ個(左の場合は４個) とすると、残りがちょうど(ｎ−ｍ)角形になっています。

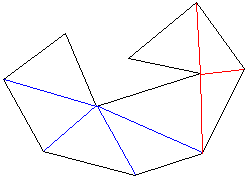残りの(ｎ−ｍ)角形もどこか頂点を選んで対角線を引いていけば、いずれ凸多角形に帰着されます。
従ってすべてのｎ角形は、交差しない(ｎ−３)本の対角線により(ｎ−２)個の三角形に分割されることがわかります。

2次形式なんで対角化できればわかりやすいかなと思ってやってみました。

NO.877
自然数a,b（a≧1,b≧1）に対して,ab|a²+b²⇔a=b

←は明らか

→
(a²+b²)/ab=n n:自然数 とおくと n=2⇔a=b より
(1) a²+b²-nab=0 が n≠2 のとき自然数解(a,b)をもたないことを示せばよい。
そこで、(1)が解(a,b)を持ったと仮定する。

x=(a+b)/2, y=(a-b)/2 とおくと、a=x+y,b=x-y これを(1)に代入すると

	a2+b2-nab
=	(x+y)2+(x-y)2-n(x+y)(x-y)
=	(2-n)x2+(2+n)y2

より
(2) (2-n)x²+(2+n)y²=0を得る。

n=1の場合、 (2)の整数解は(0,0)のみで、(a,b)=(0,0)なので a≧1,b≧1に矛盾。
n≧3の場合、(2)は (n+2)y²-(n-2)x²=0 とかけて

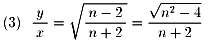
n²-4はn≧3で平方数とならないので(3)の右辺は無理数。
一方左辺は有理数なので矛盾。

ペル方程式について考えてみます。

　　　　x² − D y² = ±1 　　（D は平方数でない正整数）

と表されるディオファントス方程式をペル方程式といいます。ペル方程式において、自明な解 x = 1,y = 0 以外の最も小さい正整数解を、そのペル方程式の最小解といいます。
そこで、いくつかの D について最小解を求めてみてください。簡単に見つかるでしょうか？

皆さん！国際数学オリンピック（International Mathematical Olympiad）をご存じですか。 毎年（７月）１回、高校生（以下）の学生を対象として行われる数学の問題解決を競う 国際大会のことです。
日本は1990年の第31回国際数学オリンピック（北京）大会において初参加を果たしました。 その大会の順位は世界５４カ国の中で、 ２０位、銀メダル２人、銅メダル１人の結果でした。 今では、内容的にも規模的にも基盤の整った国際大会に発展しています。
ＩＭＯ大会は1959年より毎年夏（７月中旬）、主催国を各国持ち回りとして、 実施されている。以下ＩＭＯ大会の目的に則し、どのようにして行われるかについて、 いくつか紹介します。

1. 大会の目的と意義
   
   ＩＭＯは、学校の教材に限らない数学の問題に、特に興味をもつ少年少女のための筆記試験による コンテストである。試験の答案を比較することによって、ＩＭＯでは個々の競争者が挑戦し励ましを 得て才能を見い出し、同時に高校レベルでの国際的交流を増進することを目的としています。 またこのＩＭＯは、若人間の交友的関係の樹立の補助をし、 かくして各国間の協力と理解の増進を意図して行われる。
   
   
2. 各国の参加条件
   
   開催国より招待を受けた各国が、団長並びに副団長、と６名のを越えない選手より成るチームを 開催国へ送ることが出来る。コンテストは、開催年の７月１日時点で１８歳以下であり、 かつ高校（または中学）に在学している者でなければならない。
   
   
3. 費用
   
   主催者が、団長並びに副団長と選手の開催地到着の日より帰国出発日までのチームの食事、 宿泊および滞在に要する費用すべてを負担する。 しかし、参加各国と開催国間の往復の交通費は各テームの負担となる。 オブザーバーやチームの同伴者は全費用を自己負担することが義務づけられ、 また、主催者側がチームの同伴者と人数を制限することがある。
   
   
4. 大会日程
   
   １日目：午前団長到着、夜問題資料配付。
   ２日目：問題選定会議（討議）に入る。
   ３日目：午前午後、問題選定会議で最終的に６題を選定する。 夜、問題翻訳まず、英語・ドイツ語・フランス語・ロシア語・スペイン語に正確に訳される。
   ４日目：問題翻訳、各国団長が自国語に訳す。（選手等到着、問題漏洩を防ぐため、 試験終了まで団長と選手達の接触は禁じられる）。
   ５日目：開会式　選手には国際親善のためのプログラムが組まれる。
   ６日目・７日目：試験、各日４時間半３題、夜団長、副団長は自国の選手の採点をする。成績判定。
   ８日目：午前・午後、団長・副団長成績判定、選手、国際親善活動、夜、最終陪審員会議。
   ９日目：各国の団長・副団長　最終陪審員会議、選手、国際親善活動。
   １０日目：閉会式。
   １１日目：帰国。
   
   
5. 問題の提出
   
   参加各国は、開催日の３，４ヶ月前の定められた期日までに３から ６題の問題を解答とともに各年のＩＭＯ委員会に提出する事が義務づけられる。 提出される問題は、初等数学の異なる分野から、難易に変化がある精選されたもので、 未公開なオリジナルのものとされる。 提出するのは、英語、ドイツ語、フランス語、ロシア語の４カ国語のいずれかの言語で 記述されたものとされる。
   
   
6. 問題選定委員会
   
   
7. 各国の団長到着後、国際陪審員会が２、３日にわたって開かれる。 最初に、各年の開催国委員会によって選択され、その年の候補となっている 数十題の問題資料（すべて英語記述）が渡され、 討議は英語、ドイツ語、フランス語、ロシア語で行われ、 その年のＩＭＯ問題として、より質のよいものを選定する。
   
   
8. 問題翻訳
   
   
9. ６題の問題を選定後、まず英語の記述のものがドイツ語・フランス語・ロシア語・スペイン語に 翻訳される。次ぎに、各国の団長が自国語に翻訳する。 その後、正しくかつ公平に翻訳されたが互いに検閲する。
   
   
10. 試験
    
    試験は２日間にわたり、各日、３題が出題に対して４時間半という形式で行われる。 通常、試験会場として開催地にある大学が使われる。 各国６人の生徒はどの２人も同室にならないように分散して受験し、 筆記用具と作図用具以外のものの使用は一切禁じられている。 開始30分以内に、問題に関する質問を筆記にて自国語で質問することができる。 多くの場合は、生徒の質問については回答しない。”No Answer”である。
    
    
11. 採点と判定
    
    試験が終わると、各国の生徒の答案は、それぞれ各国の団長はならびに副団長に渡され、 彼らがこれを採点する。毎年、各問平等に７点の配点があり、１人分の満点は４２点である。 採点後、団長、副団長は答案の要点を英語に整理して、 判定団（開催国の数学研究者達によって構成されるチームがこの役にあたる） 自分たちの評価（採点の妥当性）を判定してもらう。 判定会は１回30分で、１題の問題（計６人分）について判定する。
    
    
12. 最終陪審員会
    
    判定員と各国団長との生徒の答案に対する評価の相違に裁定、 およびその年の各賞の配分について協議する。
    
    
13. 各賞の選定
    
    
14. 得点により、生徒の順位が定まり、優勝者には、金・銀・銅賞が与えられる。 金・銀・銅賞の総数は参加生徒総数の半分を超えないこと、 及び、金、銀、銅の割合は大体１：２：３であることが決められている。 また、金、銀、銅賞以外に、特に見事なオリジナルな解を出した者に、 特別賞が与えられる。閉会式で、受賞者には証書とメダルが授与されるが、 他の生徒にも、この大会参加の証書が与えられる。 なお、公式には国別順位なるものは競わないが、生徒６人分の総得点を算出し、 これを国別順位とするのが慣例になっている。
    
    
15. 日本の成績状況
    
    

    回	場所	何年	参加国数	日本順位	金メダル	銀メダル	銅メダル
    ３１	北京	１９９０	５４	２０	０	２	１
    ３２	スウエーデン	１９９１	５５	１２	０	３	３
    ３３	モスクワ	１９９２	５６	８	１	３	１
    ３４	イスタンプール	１９９３	７３	２０	０	２	３
    ３５	香港	１９９４	６９	１０	１	２	３
    ３６	カナダ	１９９５	７３	９	１	３	２
    ３７	インド	１９９６	７５	１１	１	４	０
    ３８	アルゼンチン	１９９７	８２	１２	１	３	１
    ３９	台湾	１９９８	７６	１４	１	１	３
    ４０	ルーマニア	１９９９	８１	１３	２	４	０
    ４１	韓国	２０００	８２	１５	１	２	３

    
    

参考文献：
�@数学オリンピック’９３〜９８（日本評論社）の付録Ｂ　
�A数学セミナー2000年１１月号　
�B新数学辞典：大阪書籍

この度のドメイン取得により、新しいホームページのオープン 誠におめでとうございます。これからの貴ページの益々の発展と 管理者のご活躍を心から、お祈りします。 ここで、お祝いの印しに、問題を提供します。
（１＋ｘ＋ｘ^２）^ｎの展開係数をを考えてください。

a²+b²=ｍab（ｍは自然数)とおく。
a,b一方が偶数でもう一方が奇数の場合、a²+b²=奇数、 ab=偶数となるので、両方とも奇数または偶数。
両方とも偶数、a=2A,b=2Bであれば4(A²+B²)=4mABとなり 結局もとの形に戻るのでa,bはともに奇数とする。
するとa²+b²=偶数、ab=奇数なのでm=2nとおける。
a²+b²=2nab
a²+b²-2nab=(a-nb)²+b²・(1-n²)=0
(a-nb)²=b²・(n²-1),　|a-nb|=b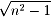
a-nbは自然数、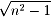は無理数なので
n=1,つまりa=bのとき a²+b²=2abとなる。

試しにいくつか展開してみました。

（１＋ｘ＋ｘ^２）^２＝ｘ^４＋２ｘ^３＋３ｘ^２＋２ｘ＋１

（１＋ｘ＋ｘ^２）^３＝ｘ^６＋３ｘ^５＋６ｘ^４＋７ｘ^３＋６ｘ^２＋３ｘ＋１

（１＋ｘ＋ｘ^２）^４＝ ｘ^８＋４ｘ^７＋１０ｘ^６＋１６ｘ^５＋ １９ｘ^４＋１６ｘ^３＋１０ｘ^２＋４ｘ＋１

パスカルの三角形を連想しますよね？
同じように係数を並べてみました。

ｎ	（１＋ｘ＋ｘ２）ｎの係数
１				１	１	１
２			１	２	３	２	１
３		１	３	６	７	６	３	１
４	１	４	１０	１６	１９	１６	１０	４	１
・・・		・・・

並べながら気づきました。 パスカルの三角形は、上２つを足していくことで形成されますが、 これは上３つの和で作っていけばいいのですね。 なーるほど。

E-mail 戻る