Weekend Mathematics/問題/問題88
88.四角形の問題
ハンガリーでのお話:
ある生徒が黒板に四角形を描きました。 ヤノスはそれを正方形だと言い、 イルメは台形だと言いました。 また、マリアはひし形だと主張し、 エファは平行四辺形だと言いました。 先生はその四角形を徹底的に研究してから、 この四つの主張のうち、三つが正しく、一つだけ間違っていることを確認しました。 生徒が黒板に書いた四角形はいったいどういう四角形だったのでしょう。
遊びの数学
ヨハンネス・レーマン著
和田秀之訳
啓学出版
解答・その1
(ペンネ-ム:杖のおじさん)
答えは ひし形です。
正方形を書いたとしたら全員が正解となってしまいます。
解答・その2
(ペンネ-ム:abcde)
ひし形は台形とも平行四辺形ともいえるからです
解答・その3
(ペンネ-ム:浜田 明巳)
もし正方形である事が正しければ,その四角形は台形でもあり,ひし形でもあり,平行四辺形でもある. これは4人とも正しい事になり,題意に反する.
従って正方形である事は間違いである.
このとき,この四角形がひし形であれば,それは台形でもあり,平行四辺形でもあるので,題意に適する.
この四角形が台形であれば,それはひし形や平行四辺形でない場合があるので,題意に反する.
この四角形が平行四辺形であれば,それはひし形でない場合があるので,題意に反する.
故に答はひし形である.
解答・その4
(ペンネ-ム:teki)
<答え> ひし形
台形、平行四辺形、ひし形、正方形は、この順に成立条件が厳しくなります。 従って、4つのうち、3つの条件を満足する図形はひし形ということになりま す。 以前に先生の問題(2001年8月、第56回 正方形?の問題)でも同様の問題がありましたね。 ベン図を描くと、台形の中に平行四辺形、その中にひし形、その中に正方形とい う具合になります。 よって、3つが正しく、1つが誤りというのは、ひし形しかあり得ません。
解答・その5
(ペンネ-ム:BossF)
{正方形}⊆{菱形}⊆{平行四辺形}⊆{台形}
ですから
答え 菱形
解答・その6
(ペンネ-ム:Toru)
{台形}⊃{平行四辺形}⊃{ひし形}⊃{正方形}
ということで、黒板に書かれた四角形が(正方形でない)ひし形とすれば、ヤノス だけが間違いで残りの3人が正しいと言うことになるのでしょう。ただどうも私には ひし形を台形とよぶのは少し抵抗があります。(ひっくり返ってしまいそうでとても 台にはなりそうもないので)
解答・その7
(ペンネ-ム:aa)
四角形の性質を上げると以下のようになる。
台形:1組の辺が平行
平行四辺形 :2組の辺が平行
長方形:4つの角がすべて等しい
ひし形:4辺がすべて等しい
正方形:4つの角が全て等しく、かつ4辺がすべて等しい
ヤノス:正方形
イルメ:台形
マリア:ひし形
エファ:平行四辺形
先生:四つの主張のうち、三つが正しく、一つだけ間違っている
書いた図形 ヤノス(正方形) イルメ(台形) マリア(ひし形) エファ(平行四辺形) 台形 × ○ × × 平行四辺形 × ○ × ○ 長方形 × ○ × ○ ひし形 × ○ ○ ○ 正方形 ○ ○ ○ ○
よってひし形。
解答・その8
(ペンネ-ム:午年のうりぼう)
正方形、台形、ひし形、平行四辺形とは以下のような四角形である。
正方形 ⇔ 「4辺の長さが等しい。かつ、4角が90°。」である四角形。
⇔ 「2組の対辺が平行である。かつ、4辺の長さが等しい。かつ、4角が90°。」である四角形。…①
台形 ⇔ 少なくとも1組の対辺が平行である四角形。…②
ひし形 ⇔ 4辺の長さが等しい四角形。
⇔ 「2組の対辺が平行である。かつ、4辺の長さが等しい。」である四角形。…③
平行四辺形 ⇔ 2組の対辺が平行である四角形。…④
したがって、
① ⇒ ②または③または④
③ ⇒ ②または④
④ ⇒ ②
であるから、
生徒が黒板に書いた四角形は、ひし形である。…(答)
解答・その9
(ペンネ-ム:三角定規)
4つの四角形の性質は,上図のように表される。 このうち3つが正しく1つが間違いということは 生徒が書いた四角形は ひし形 である。…[答]
解答・その10
(ペンネ-ム:gankopan)
答は正方形で無いひし形(4角が90度でないひし形)だと思います。
包含関係から考えると、概念的に大きなものから、
台形>平行四辺形>ひし形>正方形
となります。
典型的な台形であれば1人が正解。
典型的な平行四辺形であれば2人が正解。
典型的なひし形であれば3人が正解。
正方形であれば4人が正解となるはずです。
解答・その11
(ペンネ-ム:夜ふかしのつらいおじさん)
生徒が黒板に書いた四角形は菱形です。
一般の四角形に次のように条件を付け加えていくと最後に正方形になります。
条件1:向かい合う1組の対辺が平行
条件2:向かい合う2組の対辺が平行
条件3:内角の大きさがすべて等しい(1つの内角が直角)
条件4:辺の長さがすべて等しい(隣り合う2辺が等しい)
条件5:辺の長さがすべて等しい(隣り合う2辺が等しい) 条件4と同じ
条件6:内角の大きさがすべて等しい(1つの内角が直角) 条件3と同じ
右にある図形は左にある図形の性質を持っているので、 左の図形の名前で表しても良いわけです。 正方形は、長方形と言っても良いし、菱形と言っても良いし、 平行四辺形と言っても良いし、台形と言っても良いわけです。 次の表から答は、菱形になります。
黒板の絵が 正方形のとき 菱形のとき 平行四辺形のとき 台形のとき 主張 ヤノスの「正方形だ」は 正しい 誤り 誤り 誤り マリアの「菱形だ」は 正しい 正しい 誤り 誤り エファの「平行四辺形だ」は 正しい 正しい 正しい 誤り イルメの「台形だ」は 正しい 正しい 正しい 正しい
解答・その12
(ペンネ-ム:kenchan)
まずそれぞれの図形の性質について考えてみました。
台形は向かい合うどちらか一組の辺が平行。
平行四辺形は向かい合う二組の辺が平行。
ひし形は平行四辺形の特別な図形で、四辺共に等しい。
長方形は平行四辺形の特別な図形で、全ての角が90度。
正方形はひし形と長方形の性質を合わせたもの。
と、考えられます。これを図にまとめるとこのようになります。
この図を見るとわかると思いますが、 正方形というのは四角形の中で一番制限された図形であるとわかります。 つまり、正方形はひし形でもあり、平行四辺形でもあり、台形でもあるわけです。 ということで正方形は正解にはあたりません。
正解はひし形(ただし正方形以外)です。 ひし形は図からわかるように平行四辺形でもあり、台形でもあるのです。
解答・その13
(ペンネ-ム:anik)
台形 …………「1組の辺が平行」
平行四辺形 …「2組の辺が平行」
ひし形 ………「2組の辺が平行ですべての辺の長さが等しい」
正方形 ………「2組の辺が平行ですべての辺の長さが等しく頂点の角が直角」
よって
平行四辺形は台形を含む。
ひし形は平行四辺形と台形を含む。
正方形はひし形と平行四辺形と台形を含む。
つまりヤノス(正方形)が正しいとすると、全員が正しいことになるのでヤノスが間違っている。
つまりヤノス以外(ひし形と平行四辺形と台形)が正しいことになるので正方形でないひし形となる。
答え 頂点角が直角でないひし形
解答・その14
(ペンネ-ム:柿本 浩)
それぞれの四角形の定義を
台形 :1組の対辺が平行である四角形
平行四辺形 :2組の対辺がいずれも平行である四角形
ひし形 :2組の対辺がいずれも平行で、かつすべての辺の長さが等しい四角形
正方形 :2組の対辺がいずれも平行で、かつすべての変の長さが等しく、かつすべての内角が直角である四角形
として解答させて頂きます。
上記の定義に基づいて考えると
- 平行四辺形の定義を満たしている四角形 → 必然的に台形の定義を満たしている
- ひし形の定義を満たしている四角形 → 必然的に平行四辺形の定義を満たしている
- 正方形の定義を満たしている四角形 → 必然的にひし形の定義を満たしている
と見なす事ができます。ベン図で表すと以下の通り。
正方形 ⊂ ひし形 ⊂ 平行四辺形 ⊂ 台形 ⊂ 四角形
よって 三つが正しく、一つだけ間違っている → 三つの四角形の定義を満たし、一つの定義を満たさない となるのは「ひし形の定義を満たしているが、正方形の定義は満たしていない四角形」である事が分かり 生徒が黒板に書いた四角形は
『2組の対辺がいずれも平行で、かつすべての辺の長さが等しいが、内角は直角でない四角形』
であった事が分かります。
解答・その15
(ペンネ-ム:蜘蛛の巣城)
小学生が概念の広さ・包含関係を学ぶのに、よい教材なのでしょうね。
① 四角形(四辺形と云ってよいでしょうか。)のうちで 台形と呼ばれるのは、「1組の向かい合う2辺が平行である」ものです。
② 四角形のうちで「2組の向かい合う2辺が平行である」ものを 平行四辺形と呼びます。
この①②から「平行四辺形が台形に包含される」ことを理解できれば、あとは大丈夫なのでしょうね。
③ 平行四辺形のうちで「対角線の長さが等しい」ものを 長方形と呼び、「対角線が直交する」ものを菱形という。③から「対角線の長さが等しく、かつ直交する」正方形は、 長方形でもあり菱形でもあることを発見した小学生はきっと数学が好きになります。
正方形は、菱形でもあり平行四辺形でもあり台形でもありますから、 1つの主張だけが間違っているならばヤノスが間違っています。 従って、描かれた図形は「対角線の長さが異なる菱形」です。 菱形のうち、正方形ではないものですね、要するに。
解答・その16
(ペンネ-ム:kirkland)
先生 「時間がないから、とっとと片づけよう。」 A君 「結論から言うと、黒板に書かれた四角形はひし形で、間違えたのは正方形だと言ったヤノスです。」 先生 「正方形、ひし形、平行四辺形、台形の定義は?」 A君 「他の誰かが説明して下さるでしょうから省略です。時間ありません。」 先生 「では、正方形、ひし形、平行四辺形、台形の包含関係は?」 A君 「他の誰かがベン図を描いて下さるでしょうから省略です。時間ありません。」 先生 「何とも横着な……。」 A君 「ところで、先生。何でこんなことが起こったんでしょうかね?あっ、分かりましたよ。見る角度の問題ですね。」 先生 「??」 A君 「ヤノスは教室の一番前の端っこの方に座ってたんですよ。斜めから見たので、ひし形が正方形に見えちゃったんですよ。」 先生 「だったら台形と言った生徒は?」 A君 「イルメに関しては、次の3パターンが考えられますね。
①四角形のことについて全く分かっていない
②一番無難なのでとりあえず台形と言った
③非常に神経質なので、遠近法だとか訳の分からないことを言い出した」先生 「………。」
正解者
teki Toru 柿本 浩 kenchan anik 三角定規 gankopan BossF 浜田 明巳 abcde 夜ふかしのつらいおじさん 杖のおじさん 午年のうりぼう 蜘蛛の巣城 aa kirkland
今回の問題は、四角形の定義と、その包含関係に関する問題です。 見る角度によって違う? ということもあるかもしれませんが、 そういう趣旨ではありません。問題の趣旨がうまく伝わらなかったかな? 今月はいただいた解答が少なくて、ちょっと寂しかったです。
四角形の定義と、その包含関係について、以前第56回 正方形?の問題でもこれについて触れています。
再度、確認しましょう。四角形の中でも特殊な四角形の定義を整理してみます。
(定義と同等な性質もありますが・・・)
台形 ・・・向かいあう1組の対辺が平行 平行四辺形 ・・・向かいあう2組の対辺が平行 長方形 ・・・4角がすべて直角 ひし形 ・・・4辺がすべて等しい 正方形 ・・・4角がすべて直角、かつ4辺がすべて等しい
これらの包含関係をベン図にしてみました。
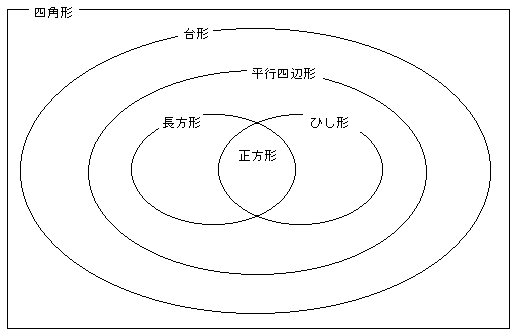
というわけで、「正方形」をもってこれは「台形」だというのは言いにくいのですが、 「台形」の条件を満たしているという意味では、立派な「台形」になります。
今回の解答は「ひし形」ですが、厳密に言えば、 「正方形でないひし形」ということになります。 おわかりですよね? 「正方形」も「ひし形」ですから。

 E-mail
E-mail
 戻る
戻る
 top
top