Weekend Mathematics乛栤戣乛栤戣56
俆俇丏惓曽宍丠偺栤戣
惓曽宍傜偟偒巐妏宍偺巻偑偁傝傑偡丅 偦傟偑惓曽宍偱偁傞偙偲傪丄巻傪愜傞偙偲偵傛偭偰妋偐傔偨偄偲巚偄傑偡丅
- 岦偐偄崌偭偨曈偺拞揰傪寢傇墶偺慄偱愜偭偨偲偙傠丄偒偭偪傝廳側傝傑偟偨丅 偦偆偡傞偲丄偙偺巐妏宍偼偳傫側恾宍偱偟傚偆偐丅
- 傕偆侾搙丄拞揰傪寢傇廲偺慄偱愜偭偨偲偙傠丄傗偼傝偒偭偪傝廳側傝傑偟偨丅 偡傞偲丄偙傟偼偳傫側巐妏宍偱偟傚偆偐丅
- 忋偺栤戣偲偼暿偺巐妏宍傪丄俀杮偺懳妏慄偱愜偭偨偲偙傠丄偳偪傜偺応崌傕偒偭偪傝廳側傝傑偟偨丅 偙偺巐妏宍偼偳傫側巐妏宍偱偟傚偆偐丅
- 巐妏宍偺巻偑惓曽宍偱偁傞偙偲傪妋偐傔傞偵偼丄嵟掅壗夞愜傟偽妋偐傔傜傟傞偱偟傚偆偐丅
悢妛僷僗儖儔儞僪乛揷懞嶰榊挊乛島択幮僽儖乕僶僢僋僗
乮儁儞僱亅儉丗kiyo乯

乮儁儞僱亅儉丗傗側偣 乯
栤戣侾乯偵偮偄偰偼 挿曽宍丄惓曽宍丄嵍塃偺曈偑摍偟偄挿偝偺戜宍
栤戣俀乯偙偆偔傞偲 挿曽宍丄惓曽宍偩偗偵側傝傑偡
栤戣俁乯偙偙偱傂偭偐偐偰偼偄偗傑偣傫乮徫乯 惓曽宍偲丄係曈偺挿偝偑摍偟偄暯峴巐曈宍乮旽宍偩偭偰偹乯
栤戣係乯偍偙偨偊偱偉乣乣偡乮帺怣偑側偄丒丒乯
媗傑傞偲偙傠丄栤偄侾乯偐栤偄俀乯偺偳偪傜偐偺忦審傪枮偨偟
側偍偐偮栤偄俁乯偺忦審傪枮偨偣偽偄偄偺偱偡偐傜
愜傝嬋偘傞夞悢偼嵟掅偱傕俀夞丄
偳偆傛偳偆傛

乮儁儞僱亅儉丗栭傆偐偟偺偮傜偄偍偠偝傫 乯
侾丂摍媟戜宍偱偡丅
岦偐偄崌偭偨曈偺拞揰傪寢傇墶偺慄偱愜偭偰丄廳側傞偲偄偆偙偲偼丄
偙偺墶偺慄偑丄曈AD丄BC偺悅捈擇摍暘慄偵側偭偰偄傞偲偄偆偙偲偱偡丅
偡傞偲丄AD // BC 偲側傝傑偡丅偙偙傑偱偱丄戜宍偲偄偆偙偲偑暘偐傝傑偡偑丄
AB偲DC傕廳側偭偰偄傞偺偱偡偐傜摍媟戜宍偵側傝傑偡丅
俀丂挿曽宍偱偡丅
岦偐偄崌偭偨曈偺拞揰偱愜偭偰廳側傟偽丄偦偺俀曈偑暯峴偲偄偆偙偲偑侾斣傛傝暘偐
傝傑偡丅俀斣偼岦偐偄崌偆俀慻偺曈偑偦傟偧傟暯峴側偺偱偡偐傜丄
偙偙傑偱偱暯峴巐曈宍偲偄偆偙偲偑暘偐傝傑偡丅
偝傜偵偙偺墶偺慄偲廲偺慄偑捈岎偟偰偄傞偺偱偡偐傜挿曽宍偵側傝傑偡丅
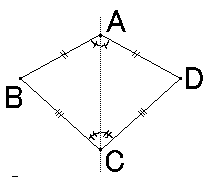
俁丂旽宍偱偡丅
懳妏慄偱愜偭偰廳側傞偲偄偆偙偲偼丄懳妏慄偑岦偐偄崌偆擇偮偺撪妏
(A偲C)偺擇摍暘慄偵側偭偰偄傞偲偄偆偙偲偱偡丅
椬傝崌偆俀慻偺擇曈 AB偲AD丄CB偲CD偑偦傟偧傟摍偟偔側傝傑偡丅
偙偙傑偱偱扂宆偲暘偐傝傑偡偑丄俀偮偺懳妏慄偱愜偭偰廳側傞偲偄偆偙偲偼丄
係曈偑摍偟偄偲偄偆偙偲偵側傞偺偱丄旽宍偵側傝傑偡丅
係丂俀夞偱偡丅
岦偐偄崌偭偨曈偺拞揰偱愜偭偰廳側傞偲偄偆偙偲偼丄
丂丂丂丂a丂椬傝崌偆俀妏偑摍偟偄乮佢A亖佢D丄佢B亖佢C乯
丂丂丂丂倐 岦偐偄崌偆俀曈偑摍偟偄乮AB亖DC乯丂偲偄偆偙偲偱偡丅
傑偨丄懳妏慄偱愜偭偰廳側傞偲偄偆偙偲偼丄BR>
丂丂丂 們 椬傝崌偆俀曈偑摍偟偄乮AB亖AD丄CB亖CD乯
丂丂丂 倓 岦偐偄崌偆俀妏偑摍偟偄乮佢俛亖佢D乯丂偲偄偆偙偲偱偡丅
倎偲倓傛傝丄係妏偑摍偟偄偙偲偑暘偐傝丄倐偲倓傛傝丄係曈偑摍偟偄偙偲偑暘偐傞偐傜偱偡丅

乮儁儞僱亅儉丗俛倧倱倱俥乯
埲壓愜傝栚偺慄傪丄幉偲屇傃傑偡

乮儁儞僱亅儉丗yokodon乯
審偺巐妏宍偺係捀揰傪帪寁夞傝偵俙丆俛丆俠丆俢偲偡傞丅
(1乯曈俙俛丄曈俠俢偺拞揰傪奺乆俵丄俶偲偡傞丅
丂戣堄傛傝丄巐妏宍俙俵俶俢偲巐妏宍俛俵俶俠偼崌摨偱偁傝丄巐妏宍俙俛俠俢偼慄暘
俵俶偵娭偟偰懳徧偲側傞丅
丂偦偺傛偆側巐妏宍偼丄摍媟戜宍丄挿曽宍丄惓曽宍偱偁傞丅乧乮摎乯
乮2乯巐妏宍俙俵俶俢偵娭偟偰摨條偺峫嶡傪偡傞偙偲偱乮曈俙俢丄慄暘俵俶偺拞揰傪
奺乆俹丆俻偲偡傞偲丄巐妏宍俙俵俶俢偼慄暘俹俻偵娭偟偰懳徧乯丄乮1乯偺俁幰偺偆
偪摍媟戜宍偺壜擻惈偼攔彍偝傟傞丅
丂摉偰偼傑傞巐妏宍偼丄挿曽宍丄惓曽宍偱偁傞丅乧乮摎乯
乮3乯偙偺応崌偼丄嶰妏宍俙俛俢偲嶰妏宍俛俠俢偑崌摨偱偁傝丄妿偮嶰妏宍俙俛俠偲
嶰妏宍俙俠俢偑崌摨偱偁傟偽椙偄丅
丂摉偰偼傑傞巐妏宍偼丄傂偟宍丄惓曽宍偱偁傞丅乧乮摎乯
乮4乯巐妏宍俙俛俠俢偑惓曽宍偱偁傞偨傔偺昁梫廫暘忦審偼丄審偺巐妏宍偑挿曽宍偱
偁傝妿偮傂偟宍偱偁傞偙偲偱偁傞丅
丂挿曽宍偼乮3乯偺忦審傪枮偨偝偢丄傂偟宍偼乮1乯偺忦審傪枮偨偝側偄偐傜丄巐妏宍
俙俛俠俢偑椉幰偺忦審傪摨帪偵枮偨偡偙偲傪挷傋傞偵偼懳妏慄偺堦曽乮椺偊偽俙俠乯
偲慄暘俵俶偵娭偟偰懳徧偱偁傞偐斲偐傪挷傋傟偽傛偄丅
丂傛偭偰丄媮傔傞夞悢偼俀夞丅乧乮摎乯

乮儁儞僱亅儉丗昹揷丂柧枻乯
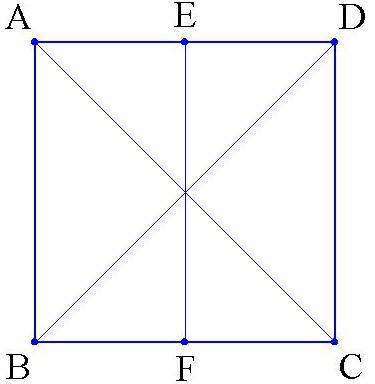
侾丏巐妏宍俙俛俠俢偵偍偄偰丆俙俢丆俛俠偺拞揰傪偦傟偧傟俤丆俥偲偡傞丏
丂俤俥傪墶偺慄偲偟乮廲丆墶偑堘偆偧丆偲偼尵傢側偄偱壓偝偄乯丆偙偺慄偱愜偭偰廳側傞偲偡傞丏
丂忦審偐傜丆俙俛亖俢俠丆佢俙亖佢俢丆佢俛亖佢俠
丂傑偨丆佢俙俤俥亖佢俢俤俥丆佢俛俥俤亖佢俠俥俤偱偁傞偐傜丆
丂丂佢俙俤俥亖佢俢俤俥亖俋侽亱丆佢俛俥俤亖佢俠俥俤亖俋侽亱
丂丂亪佢俙俤俥亖佢俠俥俤
丂丂亪俙俢//俛俠
丂屘偵巐妏宍俙俛俠俢偼摍媟戜宍偱偁傞丏
俀丏侾偐傜丆俙俢//俛俠丆俙俛//俢俠偱偁傞偐傜丆巐妏宍俙俛俠俢偼暯峴巐曈宍丏
丂傑偨佢俙亖佢俢偱偁傞偐傜丆佢俙亖佢俢亖俋侽亱
丂屘偵巐妏宍俙俛俠俢偼挿曽宍偱偁傞丏乮偙偺帪揰偱偼惓曽宍偲尷掕偡傞偙偲偼弌棃側偄乯
俁丏俙俠偱愜偭偰廳側傞偙偲偐傜丆
丂俙俛亖俙俢丆俛俠亖俢俠
丂俛俢偱愜偭偰傕廳側傞偺偱丆
丂俙俛亖俛俠丆俙俢亖俠俢
丂屘偵係曈偑摍偟偄偺偱丆巐妏宍俙俛俠俢偼傂偟宍偱偁傞丏
乮偙偺帪揰偱偼惓曽宍偲尷掕偡傞偙偲偼弌棃側偄乯
係丏侾夞愜偭偨偩偗偱偼丆柧傜偐偵惓曽宍偲尷掕偡傞偙偲偼弌棃側偄丏
丂俀夞愜傟偽丆惓曽宍偲尷掕偡傞偙偲偼壜擻偱偁傞丏偙傟傪帵偡丏
丂傑偢俤俥偱愜傝丆廳側傞偙偲偵傛偭偰丆
丂俙俛亖俢俠丆佢俙亖佢俢偱偁傞偙偲偑暘偐傞丏
丂俙俠偱愜偭偰廳側傞偙偲偵傛偭偰丆
丂丂俙俛亖俙俢丆俛俠亖俢俠
丂屘偵係曈偑摍偟偄偺偱丆巐妏宍俙俛俠俢偼傂偟宍偱偁傞丏
丂偟偨偑偭偰俙俛//俢俠偱偁傞偐傜丆摨懁撪妏偺榓偼侾俉侽亱偱偁傞丏
丂丂亪佢俙亄佢俢亖侾俉侽亱
丂佢俙亖佢俢偐傜丆佢俙亖俋侽亱
丂屘偵傂偟宍俙俛俠俢偼惓曽宍偱偁傞丏

乮儁儞僱亅儉丗judas乯
1.
巐妏宍偺捀揰傪嵍忋偐傜媡帪寁夞傝偵A,B,C,D偲偡傞丅
乽岦偐偄崌偭偨曈偺拞揰傪寢傇墶偺慄乿偱愜偭偨偲偙傠偒偭偪傝廳側偭偨偲偄偆偙偲
偼丄AB偺拞揰M偲CD偺拞揰N傪寢傇慄偱慄懳徧偲側傞巐妏宍偱偁傞丅
偡側傢偪AM亖BM丄CN亖DN丄AD亖BC丄佢A亖佢B丄佢C亖佢D丄佢AMN亖佢BMN亖佢CNM亖
佢DNM亖90亱偲側傞丅
偙傟偑惉傝棫偮偨傔偵偼巐妏宍偼摍媟戜宍偱偁傞偙偲偑昁梫廫暘忦審乮仼尵梩偺巊偄
曽偁偭偰傑偡傛偹丠乯偲側傞丅乮AB乤CD丅偮傑傝墶岦偒丅乯
2.
1.偺巐妏宍傪崱搙偼拞揰傪寢傇廲偺慄偱愜偭偨偲偙傠偒偭偪傝廳側偭偨丅乮堦搙奐偄
偰偐傜嵞搙愜傞丄偲偄偆偙偲偱偡傛偹丠乯
AD偺拞揰O偲BC偺拞揰P傪寢傇慄偱慄懳徧偲側傞丅
偡側傢偪AO亖DO丄BP亖CP丄佢A亖佢D丄佢B亖佢C偲側傞丅
1.偺忦審偲傑偲傔傞偲佢A=佢B=佢C=佢D亖90亱偲側傞丅
偟偨偑偭偰丄偙傟偑惉傝棫偮偨傔偵偼挿曽宍偱偁傞偙偲偑昁梫廫暘忦審偲側傞丅
3.
巐妏宍偺捀揰傪嵍忋偐傜媡帪寁夞傝偵A,B,C,D偲偡傞丅
懳妏慄AC丄BD偦傟偧傟偵偮偄偰慄懳徧偺巐妏宍偲側傞丅
AC偵偮偄偰丄AB亖AD丄BC亖CD丄佢B亖佢D偲側傞丅
BD偵偮偄偰丄AB亖BC丄AD亖CD丄佢A亖佢C偲側傞丅
傑偲傔傞偲丄偡傋偰偺曈偺挿偝偼摍偟偔丄岦偐偄偁偭偨妏偺戝偒偝偑摨偠巐妏宍偲側傞丅
偙傟傪枮偨偡偵偼傂偟宍偱偁傞偙偲偑昁梫廫暘忦審偲側傞丅
4.
寢榑偐傜尵偆偲2夞偱偡丅
傑偢岦偐偄崌偭偨曈偺拞揰乮廲偱傕墶偱傕傛偄乯偱愜傝丄廳側傟偽摍媟戜宍偲妋擣偱
偒傞丅
墶偱愜偭偨偲偡傞偲乮AB偺拞揰M偲CD偺拞揰N偱愜傞乯丄佢A亖佢B丄佢C亖佢D丄AD亖BC
偲側傞丅
師偵懳妏慄乮偳偪傜偱傕傛偄乯偱愜傝丄廳側傞偙偲傪妋擣偡傞丅
AC偱愜偭偨偲偡傞偲丄AB亖AD丄BC亖CD丄佢B亖佢D偲側傞丅
埲忋傪偁傢偣傞偲丄佢A亖佢B亖佢C亖佢D亖90亱丄AB亖BC亖CD亖AD偲側傝丄惓曽宍偲側
傞丅

乮儁儞僱亅儉丗奰杮丂峗乯
仠岦偐偄崌偭偨曈偺拞揰傪寢傇墶偺慄偱愜傝丄偒偭偪傝廳側傞応崌
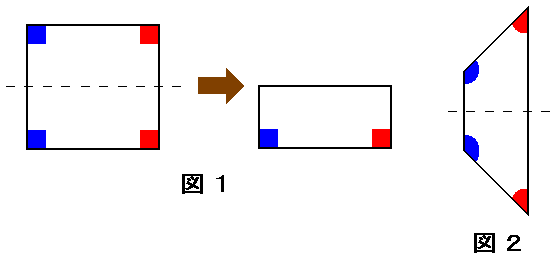 廳側傝崌偆晹暘傪峫偊傞偲丄忋壓偺椬傝崌偭偨妏偺戝偒偝偑摍偟偄帠偑暘偐傞乮恾侾乯
廳側傝崌偆晹暘傪峫偊傞偲丄忋壓偺椬傝崌偭偨妏偺戝偒偝偑摍偟偄帠偑暘偐傞乮恾侾乯
慡偰偺撪妏偑捈妏偱偁傞惓曽宍丒挿曽宍偑偙偺忦審傪枮偨偡偺偼柍榑偩偑
戜宍偱偁偭偰傕偙偺忦審傪傪枮偨偡応崌偑偁傞乮恾俀乯
傛偭偰偙偺応崌丄巐妏宍偼惓曽宍丒挿曽宍丒暯峴偱側偄俀曈偺挿偝偑摍偟偄戜宍乮摍媟戜宍乯偺偄偢傟偐偩偲暘偐傞丅
仠峏偵拞揰傪寢傇廲偺慄偱愜傝丄偒偭偪傝廳側傞応崌
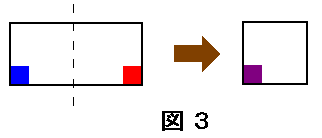 崱搙偼慡偰偺妏偑廳側傝偁偆偺偱丄慡偰偺撪妏偺戝偒偝偑摍偟偄帠偑暘偐傞乮恾俁乯
崱搙偼慡偰偺妏偑廳側傝偁偆偺偱丄慡偰偺撪妏偺戝偒偝偑摍偟偄帠偑暘偐傞乮恾俁乯
偙偺応崌丄俁俇侽亱亐係亖俋侽亱偱慡偰偺妏偼捈妏偲側傞偺偱
巐妏宍偼惓曽宍傕偟偔偼挿曽宍偩偲暘偐傞丅
仠侾杮偺懳妏慄偱愜傝丄偒偭偪傝廳側傞応崌
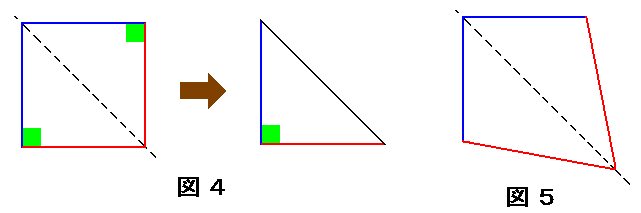 偙偺応崌偼丄懳妏慄傪嫴傫偱椬傝崌偆曈偺挿偝偲
幬傔偵岦偐偄崌偆妏偺戝偒偝偑摍偟偄帠偑暘偐傞乮恾係乯
偙偺応崌偼丄懳妏慄傪嫴傫偱椬傝崌偆曈偺挿偝偲
幬傔偵岦偐偄崌偆妏偺戝偒偝偑摍偟偄帠偑暘偐傞乮恾係乯
偨偩偟丄懳妏慄傪嫴傑偢偵椬傝崌偭偰偄傞曈乮恾係偺惵偺曈偲愒偺曈乯偺挿偝偑
摍偟偄曐徹偼側偔丄恾俆偺條側巐妏宍傕峫偊傜傟傞丅
仠俀杮偺懳妏慄偱愜傝丄偳偪傜傕偒偭偪傝廳側傞応崌
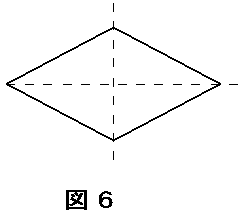 偙偺応崌偼慡偰偺曈偺挿偝偑摍偟偄帠偵側傞偑
妏搙偵惂尷偼側偄偨傔偵丄旽宍偱偁偭偰傕偙偺忦審傪枮偨偡帠偑暘偐傞乮恾俇乯
偙偺応崌偼慡偰偺曈偺挿偝偑摍偟偄帠偵側傞偑
妏搙偵惂尷偼側偄偨傔偵丄旽宍偱偁偭偰傕偙偺忦審傪枮偨偡帠偑暘偐傞乮恾俇乯
傛偭偰偙偺応崌丄巐妏宍偼惓曽宍傕偟偔偼旽宍偩偲暘偐傞丅
仛嵟掅壗夞愜傟偽惓曽宍偱偁傞帠傪妋偐傔傜傟傞偐丠
岦偐偄崌偭偨曈偺拞揰傪寢傇墶偺慄偱愜傝丄偒偭偪傝廳側傞側傜偽
惓曽宍丒挿曽宍丒暯峴偱側偄俀曈偺挿偝偑摍偟偄戜宍偺偄偢傟偐偲側傝丄
巻傪奐偄偰崱搙偼懳妏慄偱愜傝丄偒偭偪傝廳側傞側傜偽
偙偺巐妏宍偼惓曽宍偩偲暘偐傞丅
乮挿曽宍丒戜宍偼懳妏慄偱捛偭偰傕偒偭偪傝廳側傞帠偼側偄乯
傛偭偰丄嵟掅俀夞愜傟偽丄巐妏宍偼惓曽宍偩偲妋擣偱偒傞丅

乮儁儞僱亅儉丗俢俢俿乯
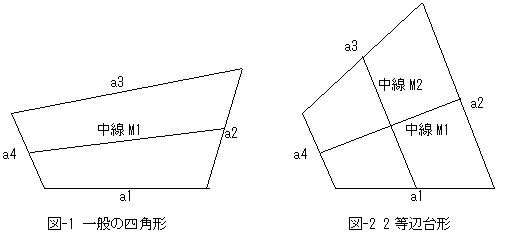
乵栤戣侾乶
恾-1偺堦斒偺巐妏宍偱丄拞慄M1偑愜傝曉偟偵娭偡傞懳徧幉偱偁傞偨傔偵偼丄
M1偼曈a2丆a4偲捈岎偡傞昁梫偑偁傞丅傛偭偰a2丆a4偼暯峴丅
偙偺忦審傪枮偨偡嵟傕堦斒揑側巐妏宍偼丄拞慄M1傪懳徧幉偲偡傞2摍曈戜宍乮恾-2乯丅
偙偺帪丄M1偱愜傝曉偡偲丄曈a1偲a3偑廳側傞偺偼柧傜偐丅
乵栤戣俀乶
恾-2偺2摍曈戜宍偺拞慄M2偑懳徧幉側傜偽丄a2亖a4丅
傑偨懳徧幉M1丆M2偵娭偟偰岦偐偄崌偆捀揰偺妏搙偼摍偟偄偺偱丄
慡偰偺捀揰妏偼摍偟偄乮360/4亖90亱乯丅傛偭偰岦偐偄崌偆曈偺挿偝偑摍偟偔丄
捀揰妏偼慡偰90亱側偺偱挿曽宍丅
乵栤戣俁乶
栤戣侾丆俀偲摨條偵峫偊傟偽丄惓傂偟宍丅
乵栤戣係乶
曗1丏巐妏宍偺宍傪堦堄偵掕傔傞嵟掅偺愜傝曉偟悢偼丄2丅
乵徹柧丠乶
巐妏宍偺捀揰傪暯柺嵗昗偱昞偣偽丄1捀揰偵2帺桼搙偱丄2亊4亖8帺桼搙丅暯峴堏摦乮帺桼搙2乯偲崉懱夞揮乮帺桼搙1乯偺擟堄惈丆憡帡恾宍偼摨堦帇偡傞偙偲偐傜乮帺桼搙1乯丄宍偩偗傪掕傔傞帺桼搙偼丄8亅2亅1亅1亖4丅
拞慄偑懳徧幉偺応崌丄椉抂揰偱曈偵捈峴偟偰偄側偗傟偽側傜側偄偺偱丄1拞慄懳徧幉偵懳偟偰丄帺桼搙偵娭偡傞撈棫側惂栺忦審偑嵟戝2屄惗偠傞乮拲丏巐妏宍偵尷傞乯丅
懳妏慄偑懳徧幉偺応崌丄椉抂揰偼丄岦偐偄崌偆2捀揰偺2摍暘慄偵側偭偰偄側偗傟偽側傜側偄偺偱丄1懳妏懳徧幉偵懳偟偰丄帺桼搙偵娭偡傞撈棫側惂栺忦審偑嵟戝2屄惗偠傞乮拲丏巐妏宍偵尷傞乯丅
傛偭偰嵟傕岠棪椙偔峴偭偰丄4/2亖2夞偺愜傝曉偟偱丄巐妏宍偺宍偼堦堄偵掕傑傞丅
乵徹柧丠 廔傢傝乶
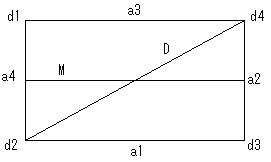 乵夝摎乶
乵夝摎乶
塃恾偺傛偆偵丄懳徧幉M丆D偑偁傞偲偡傞丅
嘆懳徧幉M傛傝丄
a1亖a3
d1亖d2
d3亖d4
嘇懳徧幉D傛傝丄
a1亖a4
a2亖a3
d1亖d3
嘊 嘆丆嘇傛傝丄
a1亖a2亖a3亖a4乮偡傋偰偺曈偑摍偟偄乯
d1亖d2亖d3亖d4乮偡傋偰偺捀揰偑摍偟偔90亱乯
嘋 嘊傛傝懳徧幉M丆D偑偁傞巐妏宍偼惓曽宍丅
曗1.傛傝丄偙傟埲忋彮側偄愜傝曉偟悢偱巐妏宍偺宍偼堦堄偵掕傑傜側偄丅
廬偭偰嵟掅2夞偺愜傝曉偟偑昁梫丅
摎偊丏俀夞

乮儁儞僱亅儉丗崅嫶 摴峀乯
(1)墶偺慄傪幉偵俀慻偺捀揰偑揰懳徧側偺偱丄摍媟戜宍
(2)2偮偺岦偐偄崌偆曈偑暯峴偱懳徧幉傪桳偡傞偺偱挿曽宍
(3)
(4)2偮丂墶偺慄丂偲丂懳妏慄丂偱愜傞丅
墶偺慄偵傛傝丄摍媟戜宍偵側傞偙偲偑傢偐傞丅
懳妏慄偱丄椬傝崌偆曈偺挿偝偑偡傋偰摨偠偵側傞丅
傂偟宍偱丄墶偺慄偱懳徧側偺偼惓曽宍

乮儁儞僱亅儉丗偹偙乯
侾丏
俙俛偺拞揰偲俠俢偺拞揰偱愜偭偨傕偺偲偡傞偲丄
佢俙亖佢俛丄佢俠亖佢俢側傞戜宍丅
俀丏
侾偺忦審偵壛偊丄佢俙亖佢俢丄佢俛亖佢俠偑惉傝棫偮偺偱丄
慡偰偺撪妏偑摨偠側偺偱丄挿曽宍丅
俁丏
侾夞栚偱俙俛亖俛俠丄俠俢亖俢俙偑惉傝棫偪丄
俀夞栚偱俛俠亖俠俢丄俢俙亖俙俛偑惉傝棫偮丅
慡偰偺曈偑摨偠挿偝側偺偱丄旽宍丅
係丏
侾偲丄俁偺侾夞栚偺寢壥傪梡偄傞偲丄
佢俙亖佢俛丄佢俠亖佢俢丄俙俛亖俛俠丄俠俢亖俢俙傛傝丄
仮俙俛俢佭仮俠俛俢偑摼傜傟丄佢俙亖佢俠丅
偟偨偑偭偰仩俙俛俠俢偼挿曽宍偱偁傞偺偱俙俢亖俛俠丅
慡偰偺曈偺挿偝偑摨偠偱偁傞偺偱惓曽宍偲暘偐傞丅
偟偨偑偭偰丄俀夞偱傛偄丅

| kiyo | 傗側偣 | 栭傆偐偟偺偮傜偄偍偠偝傫 |
| 俛倧倱倱俥 | yokodon | 昹揷丂柧枻 |
| judas | 奰杮丂峗 | DDT |
| 崅嫶 摴峀 | 偹偙 |

巐妏宍偺拞偱傕摿庩側巐妏宍偺掕媊傪惍棟偟偰傒傑偡丅
(掕媊偲摨摍側惈幙傕偁傝傑偡偑丒丒丒)
| 戜宍 | 丒丒丒岦偐偄偁偆侾慻偺懳曈偑暯峴 |
| 暯峴巐曈宍 | 丒丒丒岦偐偄偁偆俀慻偺懳曈偑暯峴 |
| 挿曽宍 | 丒丒丒係妏偑偡傋偰捈妏 |
| 傂偟宍 | 丒丒丒係曈偑偡傋偰摍偟偄 |
| 惓曽宍 | 丒丒丒係妏偑偡傋偰捈妏丄偐偮係曈偑偡傋偰摍偟偄 |
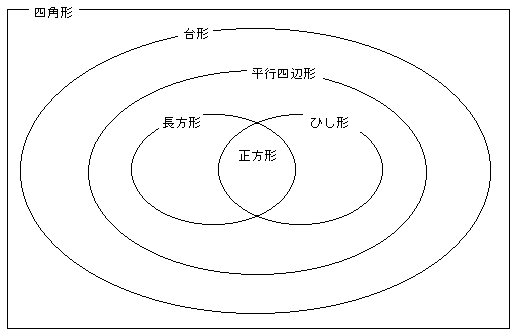
廬偭偰丄偨偲偊偽俀斣偺栤戣偱乽挿曽宍乿偲偐偗偽丄偦傟偼乽惓曽宍乿傕娷傫偱偄傞偙偲偵側傝傑偡丅
偟偐偟偁傞帪丄彫妛惗岦偗偺嶼悢偺栤戣偱丄
巐妏宍偑偄偔偮偐帵偝傟偰偄偰挿曽宍偼偳傟偱偡偐丠丂偲偄偆栤戣傪尒傞婡夛偑偁傝傑偟偨丅
夝摎傪尒傞偲丄惓曽宍偼彍偐傟偰偄傑偟偨丅
彫妛峑偺嶼悢偱偼丄偦偆偄偆巜摫側偺偱偟傚偆偐丠
巹偑嬼慠傒偐偗偨偦偺栤戣偑偄偗側偄偺偱偟傚偆偐丠
偝偰丄師偵摍媟戜宍偱偡丅
摍媟戜宍偺掕媊偼丠丂偲擸傫偱偟傑偄傑偟偨丅
乽戜宍丄偐偮暯峴偱側偄侾慻偺懳曈偺挿偝偑摍偟偄乿偱偟傚偆偐丠
偦傟偲傕乽戜宍丄偐偮暯峴側曈偺椉抂偺妏偑摍偟偄乿偱偟傚偆偐丠
偦傟偵傛偭偰丄暯峴巐曈宍偲偺曪娷娭學偑堘偭偰偒傑偡丅
壖偵摍媟戜宍偺掕媊傪乽戜宍丄偐偮暯峴偱側偄侾慻偺懳曈偺挿偝偑摍偟偄乿偲偟傑偡丅
偙傟偵偼埲壓偺(傾)丄(僀)偺傛偆側俀偮偺僞僀僾偑偁傝傑偡丅
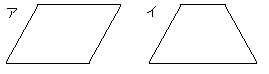
(傾)偺僞僀僾偼暯峴巐曈宍偱偡偐傜丄摍媟戜宍偼暯峴巐曈宍傪曪娷偡傞偙偲偵側傝傑偡丅
儀儞恾偱偐偔偲丄埲壓偺傛偆偵側傝傑偡丅
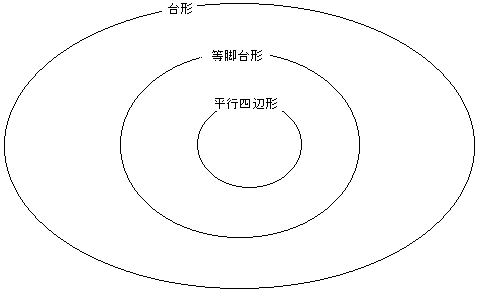
偙偺応崌丄栤戣侾偺摎偊曽偼戝曄暋嶨偵側傝傑偡丅
暯峴巐曈宍傪彍偔摍媟戜宍偲挿曽宍丄偲偄偆姶偠偱偟傚偆偐丅
堦曽丄摍媟戜宍偺掕媊偑丄乽戜宍丄偐偮暯峴側曈偺椉抂偺妏偑摍偟偄乿偲偟傑偡丅
愭掱偺恾偺(僀)偺僞僀僾偱偡丅
偙偺応崌丄暯峴巐曈宍偲偺曪娷娭學偼偁傝傑偣傫偑丄
暯峴巐曈宍偲偺岎傢傝偑偪傚偆偳挿曽宍偵側傝傑偡丅
儀儞恾偱偐偔偲丄埲壓偺傛偆偵側傝傑偡丅
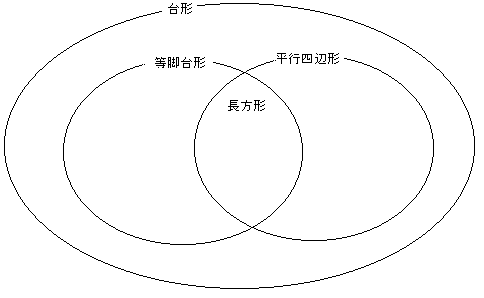
偙偺応崌偺栤戣侾偺摎偊曽偼丄摍媟戜宍偲偄偆偙偲偵側傝傑偡丅
巹偼敊慠偲慜幰偺掕媊傪僀儊乕僕偟偰偄傑偟偨丅
偱傕偙偆偟偰峫偊偰傒傞偲丄屻幰偺掕媊偑懨摉偩偲巚傢傟傑偡丅
巹偺庤尦偵偼偭偒傝偲摍媟戜宍偺掕媊偑婰弎偝傟偨傕偺偑偁傝傑偣傫丅
偳側偨偐偍傢偐傝偱偟偨傜丄嫵偊偰偔偩偝偄丅

 E-mail
E-mail
 栠傞
栠傞
 top
top