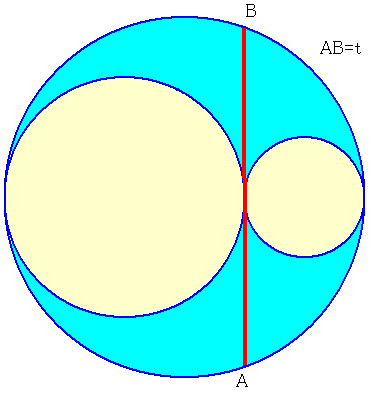
右の図は、大円とその内部に含まれる2つの小円でそれぞれ接しています。
これらによって囲まれた部分(図中のブルーに色づけした部分)の面積を求めてください。
ただし、ABは2つの小円の共通接線の一部で、その長さをtとします。
Weekend Mathematics/問題/問題87
87.3つの円に囲まれた面積
右の図は、大円とその内部に含まれる2つの小円でそれぞれ接しています。 これらによって囲まれた部分(図中のブルーに色づけした部分)の面積を求めてください。 ただし、ABは2つの小円の共通接線の一部で、その長さをtとします。
遊びの数学
ヨハンネス・レーマン著
和田秀之訳
啓学出版
解答・その1
(ペンネ-ム:19才のウメ)
tが直径の円において{(t/2)2ー2・(t/4)2}π=t2・(π/8)かも
解答・その2
(ペンネ-ム:kirkland)
A君 「ABの長さがトンっていうのは何ですか?」 先生 「???まぁ、君は気にせずABの長さが1cmということでやりたまえ。」 A君 「AB=1cmにしても、ちゃんと答えは出ますか?」 先生 「もちろん。」 A君
よし、それさえ分かれば、こんなの簡単ですよ。いやぁ、3つの円の半径がそれぞれ何cmなのか分からないので 困ってたんですよ。にも関わらず答えがきちんと出るということは、円の半径をどのように設定してもOKなわけ ですよね。ということで分かりやすく、大円の半径を0.5cm、2つの小円の半径を0.25cmと勝手に決めてしまっ て(右図)、0.5×0.5×3.14-(0.25×0.25×3.14)×2=0.3925cm2で~す!!」
先生 「限りなくインチキ臭いが、まぁそんなもんでいいんじゃないの。」 A君 「インチキだなんて心外だなぁ。では、まともなやり方を教えて下さいよ。」 先生 「中学3年ぐらいの内容なので、小学生の君には無理だよ。」 A君 「先日、小学校の卒業式があったんで、4月からは中学生なんですけど。」 先生 「ふふふっ、あきらめなさい。諸事情により君は来年も小学6年生なんだよ。」 A君 「……。」
解答・その3
(ペンネ-ム:玉村太郎)
面積 S=πt2/8
解答・その4
(ペンネ-ム:kiyo)
円周角、ピタゴラスの定理より、
(t2/8)π
です。
解答・その5
(ペンネ-ム:浜田 明巳)
こんなのになってしまいました.参加することに意義があると思ったので.
解答・その6
(ペンネ-ム:anik)
2つの小円の半径をx,y(x≧y)、大円の中心をOとおき、
小円はABの中点で交わっているので、そこをCとおき、
求める面積をSとおくと、
S=π(x+y)2-πx2-πy2=π2xy……①
AC=t/2……②
OA=x+y……③
OC=大きい方の小円の直径-大円の半径
=2x-(x+y)
=x-y……④
△AOCは直角三角形なので、ピタゴラスの定理から
OA2=AC2+OC2
②、③、④から
(x+y)2=(t/2)2+(x-y)2
x2+2xy+y2=t2/4+x2-2xy+y2
4xy=t2/4
xy=t2/16
①に代入
S=πt2/8
解答・その7
(ペンネ-ム:Toru)
2つの小円の半径を左からR1,R2 とすると 大円の半径はR1+R2となるので求める面積Sとすると
S=π(R1+R2)2-πR12-πR22=2πR1R2
一方、ABの中点をMとしMをとおりABと垂直な直線を引き、大円との交点を左 からP、QとするとΔPQBが直角三角形であることから、ΔPMBとΔBMQが相似 となって、
PM:MB=BM:MQすなわち2R1:t/2=t/2:2R2 よって4R1R2=t2/4
これを上の式に代入すれば、S=πt2/8 ----答え
ABの長さを決めてしまえば大円の半径を変えてもSが変わらないところがちょっ と不思議ですね。
解答・その8
(ペンネ-ム:aa)
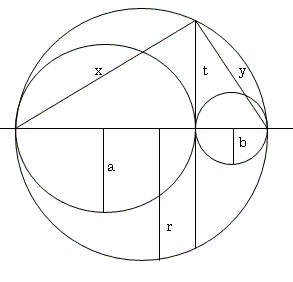
大きな円の半径をr、左の小円の半径をa、右の小円の半径をbとすると、
求める面積Sは、
S= πr2-πa2-πb2 =π(r2-(a2+b2)) ------ (1)
になります。
各辺の長さを図のように仮定すると、三平方の定理より、
x2=(2a)2+(t/2)2 ----- (2)
y2=(2b)2+(t/2)2 ----- (3)
(2r)2=x2+y2 --------- (4)
となる。
4a2+4b2+2(t/2)2=4r2
これより、
a2+b2=r2-t2/8
(1)に代入して、
S=π(r2-r2+t2/8)=πt2/8
解答・その9
(ペンネ-ム:蜘蛛の巣城)
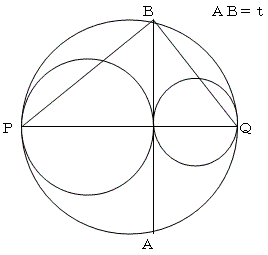
ABの中点をMとすると
点MはPQ上にも存在する。
点Mは二つの小円の接点でもある。
△BPQ、△BPM、△BQMは
それぞれ直角三角形である。
まあ、この辺は認めてしまいましょう。
三平方の定理から
PQ2=BP2+BQ2 ・・・①
BP2=BM2+PM2 ・・・②
BQ2=BM2+QM2 ・・・③
式②③を①に代入
PQ2=2BM2+PM2+QM2 ・・・①
即ち
PQ2-PM2-QM2=2BM2 ・・・④
大円と二つの小円の半径をそれぞれ r1, r2, r3とすれば
すなわち
・・・⑤
ところで求める面積は
S=π(r12-r22-r32) ・・・⑥
(0<t≦2r1)
解答・その10
(ペンネ-ム:k.cognitive)
小円をそれぞれC,Dとし、それらの直径の長さをそれぞれa、bとする。
大円の半径は1/2×(a+b)となり (a+bは大円の直径だから)
大円の中心と直線ABとの距離は a-1/2×(a+b)である
(b-1/2×(a+b)としても後の結果は同じ。 円の中心がどこにあるかで場合分けする必要があるが今は小円の大きなほうをCとした)
今ABの中点、大円の中心、点Aを頂点とする三角形を考えると、三平方の定理より以下の式が成り立つ
1/4(a+b)2=1/4×t2+1/4×(a-b)2
これより
ab=1/4×t2 ...①
を得る。 今求める面積は 大円の面積ーCの面積ーDの面積であるから
1/4×(a+b)2πー1/4×a 2πー1/4×b2π =1/2×ab π
①を代入して1/8×t2πが求まる。(答)
解答・その11
(ペンネ-ム:高橋 道広)

この問題はmennseki1のような問題を知っていたので興味を持ちました。 mennseki1の問題は AB = tのとき面積を求めよ という問題です。
さて今回の問題は 中の円の大きさを同じと考えるとABが直径で
(t/2)2π - 2×(t/4)2π = πt2/8
となります。これが答です。
まじめに計算すると次のようになります。
中にある大きいほうの円の半径をa 小さい方の円の半径をbとすると
外の円の半径は a+b 三角形OBHで OH = a+b-2b = a-b OB = a+b より
(AB/2)2 = (a+b)2 - (a-b)2 = 4ab
ab = t2/16
となります。 面積は
(a+b)2π - a2π - b2π = 2πab = 2π×t2/16 = πt2/8
となります。
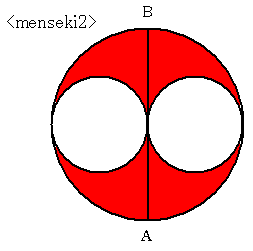
解答・その12
(ペンネ-ム:yokodon)
円の半径を小さい順に r1 , r2 , R とし、求める面積を S とすると、
r1 + r2 = R ・・・[1]
S = π・R2 - {π・(r1)2 + π・(r2)2} ・・・[2]
は直ちに分かります。
ところで、半径最大の円の中心をO、線分ABの中点をMとすると、△OAMは直 角三角形なので、
OM=√(R2 - (t/2)2) = R - 2・r1 = 2・r2 - R
が成り立ちます。これより、
(r1)2 = R・r1 - (t/4)2 、(r2)2 = R・r2 - (t/4)2
を得ます。以上を S の式 [2] に代入し、[1] を用いると、
S = π・R2 - π{R・(r1 + r2) - 2・(t/4)2} = π・R2 - π{R2 - (t2)/8} = π/8・t2
となります。
何だか、「へぇ~」な結果ですね。
解答・その13
(ペンネ-ム:teki)
答え 1/8*π*t2(ABを直径とする半円の面積)
中の小円の半径を、r1、r2とすると、大円の半径は、 r1+r2となります。 また、大円の中心をO、2つの小円の接点をCとすると、三角形OCAは直角三角形 となります。 よって、三平方の定理から、
1/4*t2+(r1-r2)2 =(r1+r2)2
が成り立ちます。つまり、
r1*r2=1/16*t2
となります。一方、水色の部分の面積は、
π*(r1+r2)2-π*r12-π*r22=2*π*r1*r2 =1/8*π*t2
となります。
解答・その14
(ペンネ-ム:kenchan)
(解答)
大円の半径をL、二つの内接する円の半径をR、r (R>=r)とする。
また図のように点C、D、E、Fを定める。ただしC、D、Fは各円の中心である。
三角形BDEは直角三角形なので三平方の定理より次が成り立つ。
BD2 = DE2 + BE2
L2 = (2R-L)2 + (t/2)2
これを整理すると
R(L-R) = (t2)/16 (1)
となる。
一方 2R+2r = 2L すなわち R+r = L も成り立つ。 (2)
これらを使って面積を求めていくことにする。
求める面積をSとすると、Sは大円の面積から二つの内接する円の面積を引けばいいので、
S = π・L2 - (π・R2+π・r2) = π・{L2-(R2+r2)} = π・{(R+r)2-R2-r2} (1)を利用 = π・(R2+2Rr+r2-R2-r2) = π・2Rr = π・2・R(L-R) (1)を利用 = π・2・t2/16 (2)を利用 = π・t2/8
よって求める面積は π・t2/8 となる
解答・その15
(ペンネ-ム:UnderBird)
線分ABの垂直二等分線は、大円および2つの小円の中心を通る。 ここで垂直二等分線と大円との交点をP,Qとすると三角形PBQは∠B=90°の直角三角形 であり、また、2つの小円の半径をそれぞれR,rとすると、PQ=2(R+r)である。 よって三平方の定理より
PQ2=PB2+QB2から、
(2R+2r)2={(2R)2+(t/2)2}+{(2r)2+(t/2)2}
よって、rR=(t2)/16
求める部分の面積は
S=π{(R+r)2-r2-R2}=2πrR=(πt2)/8
解答・その16
(ペンネ-ム:ドモン)
大円に接する2つの小円のうち,大きいほうと大円との接点をC, 小さいほうと大円の接点をDとし,大きいほうと小さいほうとの接点をEとする。
C,D,Eは大円の直径上にあるので,△ACE∽△DBEが成り立つ。 (証明は省略)よって,
AE:DE=CE:BE…①
また,大きい小円の半径をR, 小さい小円の半径をrとすると,大円の半径はR+rとなり, 求める図形の面積をSとすると,
S=π(R+r)2-πR2-πr2=2πRr…②
ここで,AE=t/2 BE=t/2 CE=2R DE=2rで①より,
t/2:2r=2R:t/2からRr=t2/16…③
よって③を②に代入すると求める解はS=πt2/8
解答・その17
(ペンネ-ム:巷の夢)
今三つの円を大円、中円及び小円とし、大円と中円の接点をC、 大円と小円の接点をD及び中円と小円の接点をEとします。 更に、大円、中円そして小円各々の直径をX,Y,Zとします。 すると三平方の定理から △BCEに対し、
BC2=Y2+(t/2)2
が成り立ちます。 同様に、△BDEに対し、
BD2=Z2+(t/2)2
又、△BCDに対し、
CD2=X2=BC2+CD2
が成り立ちます。 即ち、
X2=Y2+(t/2)2+Z2+(t/2)2
が成り立ちます。 これより
X2-Y2-Z2=t2/2
ところで、求める面積Sは
S=π(X2-Y2-Z2)/4
であるから、πt2/8が求める面積である。
解答・その18
(ペンネ-ム:午年のうりぼう)
解答・その19
(ペンネ-ム:杖のおじさん)
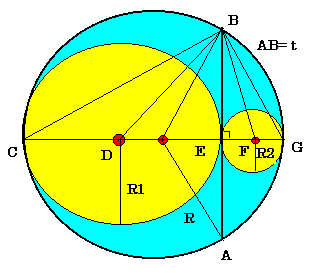
答え S=π/8・t2 です。
求める面積をS,大円の半径をR、二つの小円の半径をR1,R2とすると
S=R2・π―R12・π―R22・π……①
2・R=2・R1+2・R2……②
図形の△CBGは直角三角形、AB=tなので次の式が成り立ちます。
t/22=2・R1・2・R2……③
②の両辺を2で割る
(R1+R2)2=R2……④
③の両辺を2で割る
2・R1・R2=t2/8……⑤
上の式④から⑤を引く R12+R22=t2/8……⑥
これ等の式を①に代入すると
S=t2/8・π=π/8・t2
解答・その20
(ペンネ-ム:三角定規)
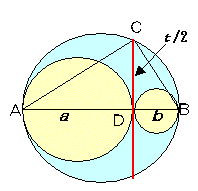
右図のように AD=a,BD=b とする。
△ACD∽△BCD より
水色部分の面積 S は,
弦の長さが一定ならば内側の2円の直径a,b が異なっても水色部の面積が一定になるのは, 式の上ではそのとおりでも,下図を素朴に見ると不思議ですよね。
もしや,赤線の左右は面積が等しいのか? 調べてみましたが,そこまではいかないようですね。 もひとつ,水色部分の重心は赤線上にあるのか? ここまでいったら神秘なのですが,これも,そうではないようです。
解答・その21
(ペンネ-ム:SOU)
以下回答
## 求める面積をSとし、最も大きな円、次に大きな円、最も小さな円の面積をそれ ぞれ、S1、S2、S3とし、 円の半径をそれぞれr1、r2、r3とする。
## S2とS3の接点における共通接線をTとし、 S1とTとの交点をそれぞれT1、T2とする。
## S1とS2の接点をT3、 S1とS3の接点をT4、 S2とS3との接点をT5とする。
回答1
S2とS3はS1に内接している ⇔ S1とS2(S3)は接点における共通接線をもつ ⇔ その共通接線に対しS1、S2(S3)の中心から下ろした垂線は重なる ⇔ S1の垂線はS1の中心を通るのでS2(S3)の垂線もS1の中心を通る ⇔ S2とS3の直系をつなげたものは、S1の直径である ⇔ S2とS3の接点はTを2分する ⇔ r1 = r2 + r3 ①
S = S1 - S2 -S3 = π { (r1)2 - (r2)2 - (r3)2} (①より) = 2π * r2 * r3 ②
ここで、
△T1T3T4 ∽ △T1T4T5 ⇔ 2 * r2 : { 4*r22 + t2/4 }2 = { 4*r22 + t2/4 }2 : 2 ( r2 + r3 ) ⇔ r2 * r3 = t2/16 ③ ②、③より、 S = πt2/8 //
回答2
S2とS3はS1に内接している ⇔ S1とS2(S3)は接点における共通接線をもつ ⇔ その共通接線に対しS1、S2(S3)の中心から下ろした垂線は重なる ⇔ S1の垂線はS1の中心を通るのでS2(S3)の垂線もS1の中心を通る ⇔ S2とS3の直系をつなげたものは、S1の直径である ⇔ S2とS3の接点はTを2分する ⇔ t = 2r ①
S2 = π/4{r1 + [r12 - (t/2)](1/2)}2
S3 = π/4{r1 - [r12 - (t/2)](1/2)}2
S1 = πr12 - π/4{r1 + [r12 - (t/2)](1/2)}2 - π/4{r1 -[r12 - (t/2)](1/2)}2
= πt2/8 //
回答3
③を用いて、Sはr2、r3に依存しないことがいえるので、 2つの内接円の半径を同じに してもよく、それを踏まえて考えると簡単に出せる。答えは同じです。
解答・その22
(ペンネ-ム:Mr.X)
外側の円の半径をRとして
tだけで決まるとはスゴイですね。
解答・その23
(ペンネ-ム:えいぶ)
大円の半径をrとする。
Bを(rcosθ,rsinθ)で表せばAは(rcosθ,-rsinθ)である。
ゆえにt=2rsinθ
右小円の半径はr(1-cosθ)/2である。
また左小円の半径はr(1+cosθ)/2である。
ゆえに求める面積は
πr2-[π{r(1+cosθ)/2}2+π{r(1-cosθ)/2}2]
であり整理して
=πr2sin2θ/2
これはπt2/8と同値である。
答え.πt2/8
解答・その24
(ペンネ-ム:小学名探偵)
答え πt2/8
3つの円の直径を、r、s、v(rが大きな円の直径)とすると、r=s+vです。
ブルーの面積 =大円Rの面積-左円Sの面積-右円Vの面積 =π/4{(s+v)2-s2-v2} =πsv/2
この問題は、ABが一定である限り、大円Rの大きさにかかわらず、 内接円の直径sとvの積が一定(ABの関数、多分2次関数)になると 主張しているようです。 実際にそうなります。
いま、ABに直交し、3つの円の中心を通る直線を引き、
この直線とABとの交点をP、
Pよりsだけ左にある点(直線と円周との交点)をC、
Pよりvだけ右にある点(直線と円周との交点)をD、
とします。 CDは大円Rの直径なので∠CADは直角です。 Pは直角三角形CABの頂点Aから斜辺CDにおろした 垂線の足なので、 直角三角形CPAと直角三角形APDは相似です。すなわち、
CP:PA=AP:PD
これは、
s:t/2=t/2:v
したがって、
sv=t2/4
ブルーの面積(πsv/2)= πt2/8
になり、sとvの比にかかわらず、一定です。
一般に、円内または円外の点Pで交わる2直線と円との交点をA,Bおよび C,Dとすると、 三角形PCAと三角形PBDは相似なので、 PC×PD=PA×PBが成立します。C=Dならば、PC2 すなわち、ある半径の円に対して点Pを決めれば、円との交点の位置によらず 交点までの距離の積が一定になります。 本問はこの特別の例であり、PC×PD=t2/4になるのでした。
解答・その25
(ペンネ-ム:WU)
A,Bの中点をC,ABに垂直の大円の直径をP,Qとする.
P側の中の円の半径をR,Q側のそれをrとすると,
AB,PQに関する方べきの定理より,
2R・2r=(t/2)2
これを使い,求める面積Sは
S=π((R+r)2-(R2+r2))=πt2/8
半径とtの関係はピタゴラスの定理や円の方程式からも出せますが,
方べきの定理(相似)が最も早いかな?
ただ,この結果の意味する
円だとした場合の半径を表すt/2(3/2)の長さの意味は何だろう?
解答・その26
(ペンネ-ム:夜ふかしのつらいおじさん)
答は、πt2/8です。
この問題は3つの円の中心が同一直線上にあるとして考えます。 そうでないと、変数tだけを用いて面積を表せないからで
図1で、CEを直径とする円の半径をa、EDを 直径とする円の半径をbとします。すると、CDを 直径とする円の半径は (a+b) となります。 求める部分の面積をSとすると、
S =(a+b)2 π - a2 π - b2 π =2abπ ・・・ ①
ここで、∠CBDは直径に立つ円周角なので直角、 ABが2つの小円の共通接線なので AB⊥CD 、 などから、△CEB ∽ △BED 。
よって、 CE:EB = BE:ED をa、b、tを用いて表すと、
図1 2a:t/2 = t/2:2b 。
∴ 2ab=t2/8 ・・・ ②
②を①に代入すると、S=πt2/8 となります。
さて、相似である図形の面積は、対応する辺の長さの2乗に比例するという関係があります。 円、正方形、正3角形などは、半径や1辺を指定すれば、 面積はその長さの2乗に比例します。よってブルーに色づけされた部分の面積は、
(a+b)2 - a2 - b2 = 2ab
に比例します。(図2) 面積の値そのものは、比例定数を掛けることで得られます。図2
正解者
kenchan teki ドモン 巷の夢 小学名探偵 UnderBird Mr.X yokodon Toru 高橋 道広 浜田 明巳 杖のおじさん k.cognitive kiyo 玉村太郎 WU 19才のウメ anik 蜘蛛の巣城 aa 夜ふかしのつらいおじさん えいぶ kirkland SOU 三角定規 午年のうりぼう
今回、特にたくさんの方から解答をお寄せいただきどうもありがとうございました。
A君もどらえもんに出てくるのび太くんと同じように 来年もまた小学生ということで安心しました!? ところで、A君の解答ですけれど、 「3つの円の半径がそれぞれ何cmなのか分からないにも関わらず答えがきちんと出るということは、 円の半径をどのように設定してもOK」という読みはなかなか深いのですが、 結果的にはそれも正しいのですけれど、その裏付けがないと厳しいと思います。 小学生だとやはりちょっと無理だったかな・・・。大人の方達の解答をみると、三平方の定理を用いるか、相似を用いるか、 それを一般化した方べきの定理を用いるかして求めていただきました。この問題の場合は、 方べきの定理を使うと早いかなと思うとともに、方べきの定理ってこういうことだったのねと 納得しますね。
方べきの定理については、問題44 ハスの問題で ご紹介しましたが、改めて。
図1
方べきの定理(図1)
定円Oと定点Pについて、PA・PB=一定
図2方べきの定理の簡単な証明をします。(図2:点Pが線分AB上にあるとき)
PA・PB =(AM-PM)・(AM+PM) =AM2-PM2 =(OA2-OM2)-(OP2-OM2) =OA2-OP2 =一定 点Pが線分AB上にない場合も同様に証明ができます。
図3方べきの定理を別な形で表現します。(図3)
1つの円に弦AB,CDがあり、その交点をPとすると、以下の等式が成り立つ。
PA・PB=PC・PD
結果的には、内側の円2つの半径によらず、tの値のみで面積が決定されるというA君の読みは正しかったわけです。 なかなかおもしろい結果だなあと思います。
さらに、夜ふかしのつらいおじさんがおもしろい考察を寄せていただきました。 なかなか美しいと思いませんか?

 E-mail
E-mail
 戻る
戻る
 top
top