Weekend Mathematics/問題/問題71
71.カーニバルのさいころ遊び
カウンターの上には、1、2、3、4、5、6と数字の入った6つのます目が用意されています。 プレイヤーは、どれでも好みのます目の1つに好きなだけお金をかけます。そして3個のサイコロを振ります。もし1つのさいころだけに自分の数字が出たら、かけたお金プラスそれと同額のお金がもらえます。もし2個のさいころに自分の数字が出たら、かけたお金プラスその2倍のお金が、そして3個のさいころ全部に自分の数字が出たら、かけたお金プラスその3倍のお金がもらえるます。もしどのさいころにも自分の数が出なければ、もちろん胴元にお金をとられてしまいます。 さあ、あなたはこのさいころ遊びに参加しますか?
1 2 3 4 5 6
サム・ロイドのパズル百科
マーチン・ガードナー編 田中勇訳
白揚社
(ペンネ−ム:サダちゃん)
賭ける金額を1とします。
3つが賭けた目にでる確率は、1/6 x 1/6 x 1/6 で配当は、4です。
計算を簡単にするために、216( 6 x 6 x 6 )回投げた(分母)として、
期待値(分子)を計算すると4になります。
同様に2つが賭けた目にでる確率は、1/6 x 1/6 x 5/6 x 3 で配当は、3です。
期待値は、45です。
また、1つが賭けた目にでる確率は、1/6 x 5/6 x 5/6 x 3 で配当は、2です。
期待値は、150です。
つまり、216という支払いに対して、199のリターンとなり、
収益率は、199/216 = 0.92....となります。
よってこの賭けには参加しない、が正しい解答です。

(ペンネ−ム:三角定規)
[答] ゲームに参加しない
自分が賭けた数と3つのサイコロの目が

掛け金をN円とすると,ゲーム後の期待賞金額は,

掛け金額より期待賞金額が少ないので,ゲームに参加しない。

(ペンネ−ム:スモークマン)
期待値が1以上になればよいが、
2*3C1*(1/6)*(5/6)*(5/6)+3*3C2*(1/6)*(1/6)*(5/6)+4*(1/6)*(1/6)*(1/6)=
(50*3+15*3+4)/216=199/216 <1なので、
割に合わない!

(ペンネ−ム:理一郎坊ちゃん)
(答)私はこのゲームには参加しません。
k(1≦k≦6)に賭けたとき、振ったサイコロのうち
3個ともkの目が出る確率は、P(3)=(1/6)3
2個だけkの目の出る確率は、P(2)=3C2*(1/6)2*(5/6)=15*(1/6)3
1個だけkの目の出る確率は、P(1)=3C1*(1/6)*(5/6)2=75*(1/6)3
kの目が1個もでない確率は、P(0)=(5/6)3=125*(1/6)3
N円を賭けたときの期待値を求めると、
E=4N*P(3)+45N*P(2)+150N*P(1)=(199/216)N<N
期待値が現在の所持金を下まわるので、私はこのゲームには参加しません。

(ペンネ−ム:Banyanyan)
どの数字にかけても同じなので、たとえば1にかけたとする。
(なぜ同じかの説明はパス)
1が1個でる確率は 5×5×3/216
1が2個でる確率は 5×3/216
1が3個でる確率は 1/216
かけたお金が何倍になってもどってくるのかの期待値を計算すると
| (1+1)×5×5×3/216+(1+2)×5×3/216+(1+3)×1/ 216 | |
| = | 199/216倍 |

(ペンネ−ム:夜ふかしのつらいおじさん)
参加しません。
サイコロの目が自分のかけた数字と同じ確率は(1/6)、違う確率は(5/6)です。
さて、x円をかけたとすると、参加したときの期待金額Eは、
| E | =0x・3C0・(5/6)3 + 2x・3C1・(1/6)(5/6)2 +3x・3C2・(1/6)2(5/6)+ 4x・3C3・(1/6)3 |
| =(199/216)x | |
| ≒0.9213x |

(ペンネ−ム:かつ)
今回の問題は。
やりません。お金の取られる可能性のあるものはやりたくないです。ばくちはあ
まりしません。(笑)
なんて投稿してもせっかくの数学について考えましょうというものなのに、そん
な理由じゃ納得できませんよね。
なので1から6までのどこかにa円かけたときの期待値を調べることにしました。
当然まずどこにかけるかという問題ですが、これはどこにかけても結果は同じな
ので一ヶ所に数字を決めた上で期待値を求めることですから数字は適当に決めま
しょう。
数字:3
さて、後は3つのさいころを振るだけです。
3つのさいころを振っての確率を求めましょう。
1.3がひとつも出ない。(はずれ)

2.3が3つのうちひとつだけ。(2倍返却)

3.3が3つのうち二つでる。(3倍返却)

4.3が3つとも出る。(4倍返却)

となります。
さぁ、準備は整いました。後は期待値を求めましょう。

となります。
つまりかけたお金a円より期待値は低いということになります。
なので、やればやるほど損してしまうかもしれない。
だからやりません。

(ペンネ−ム:kiyo)
賭ける金額を1とする。
戻ってくる金額の期待値
2*(3*(1/6)*(5/6)*(5/6))=25/36
3*(3*(1/6)*(1/6)*(5/6))=5/24
4*(1*(1/6)*(1/6)*(1/6))=1/54
| 25/36+5/24+1/54 | =(150+45+4)/216 |
| =199/216 |
したがって、確率的にはこのさいころ遊びに参加しない方が望ましい。
しかし、やって見ないと判らないので1回は参加するかもしれない。
パチンコに嵌る心理。

(ペンネ−ム:TAKE)
教科書通りの解き方です。あまりおもしろくなくてすいません。
(3つのさいころを振る)=(1つのさいころを3回振る)
つまり,反復試行の確率の計算で求められます。
※反復試行の確率
1回の試行で,事象Aの起こる確率をpとする
このとき,この試行をn回行う反復試行において,
事象Aがちょうどr回起こる確率は,
nCrprqn-r
これを使うと,

よって,a円をかけたときのもらえる金額の期待値は,
となり,かけた金額より少ない金額しか返ってこないと考えられます。

よって,計算上では参加しない方がよいのですが,私の性格上,
いちかばちか,参加するでしょう。

(ペンネ−ム:やなせ)
狙った目が出ない確率を求めれば簡単でした。
つまり狙った目が3個出る確率は1/6*1/6*1/6=1/216
この逆が目のでない確率だから5/6*5/6*5/6=125/216
これから解るように50%以上の確率で出ません。
ただし、勝負に勝つか負けるかは配当倍率の関係もあるので
狙った目の回数*配当倍率の合計が216より多い場合は勝ち
少ない場合は負けです。
そこで、狙った目が
1個だけ出る場合の確率は 回数*配当倍率=賞金?
(1/6*5/6*5/6)*3=75/216・・・・・・・75*2=150
↓
(1/6*5/6*5/6)*(5/6*1/6*5/6)*(5/6*5/6*1/6)=(1/6*5/6*5/6)*3
2個出る確率は
(1/6*1/6*5/6)*3=15/216・・・・・・・15*3=45
3個出る確率は
(1/6*1/6*1/6)*1=1/216・・・・・・・・1*4=4
150+45+4=199・・199<216なので負けですよね
いやはや、何でこうなるんだろう???
確かに全ての数字の組み合わせを作成して確かめたところ
みんごと一致・・でもさ、今月の問題は”あなたはこの勝負に
参加しますか?”だったので”参加する”でも良かったのでは?
確かに参加理由が間違っていましたがね。ちょいマイナスでも
遊べればいいんじゃないかな(笑)
6個サイコロを使ったらどうなるのかな?なんて思ってやってみました ルールは出目が存在した時は掛け金×出目の数の払い戻しです。 これだとイーブンになってしまいました。
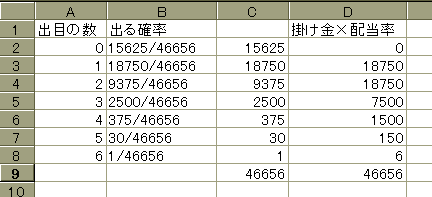

(ペンネ−ム:こざっぱ)
仮に1000円を賭けるのだとします。
まず、算数的に期待値で考えるのなら、
(以下で3C1、3C2、3C3は組み合わせの数をあらわす記号です。
3個から1個とった組み合わせ数などですね)
はずれた場合 0円×(5/6)×(5/6)×(5/6)=0
1個あたり場合 2000円×3C1×(1/6)×(5/6)×(5/6)=150000/216
2個あたり場合 3000円×3C2×(1/6)×(1/6)×(5/6)=45000/216
3個あたり場合 4000円×3C3×(1/6)×(1/6)×(1/6)=4000/216
| 合計(期待値) | =199000/216円 |
| =921.3円 |
別の考え方として、損をする確率が少しでも多いのなら参加しない、
勝つか確率が少しでも多いのなら金額を度外視しても参加する!と考えるならば、
はずれる確率を考えます。はずれる場合の確率は、
(5/6)×(5/6)×(5/6)=125/216=0.5787...
負ける確率が50%を超えています。やっぱり参加しないほうがよさそうです。
おもしろいのは、3個とも数字が出た場合にもらえる金額を4000円ではなくて、40000円に増やしてみます。
その場合の期待値は、約1088円になります。この場合、期待値が1000円を超えるので、「参加する」が答えになる気がします。でも、負ける確率は相変わらず約58%です。
この場合は参加したほうが良いのでしょうか、参加しないほうがよいのでしょうか。

(ペンネ−ム:浜田 明巳)
いつものように,エクセルのマクロで解きました.
1回かけたときの儲けの金額の期待値を計算すると,かけた金額の
-17/216≒-0.078703704
倍になることが分かる.したがってかけません.もっとも私はいかなるギャンブルもやりませんので,やるやらないの答は初めから分かっているのですが.
ちなみに,これは実際に計算したときの値
{3×1+2×5×3+1×52×3+(−1)×53}/63=−17/216
に一致します.
Option Explicit
Sub Macro1()
Sheets("Sheet1").Select
Dim a(3) As Integer
Dim kosuu As Integer
Cells(1, 1).Value = 0
Call check(1, a())
kosuu = Cells(1, 1).Value
Cells(kosuu + 1, 5).Value = "=SUM(E1:E" + strr(kosuu) + ")"
Cells(kosuu + 1, 6).Value = kosuu
Cells(kosuu + 1, 7).Value = "=E" + strr(kosuu + 1) + "/F" + strr(kosuu + 1)
Range("G" + strr(kosuu + 1)).Select
End Sub
Sub check(ByVal n As Integer, ByRef a() As Integer)
Dim atari As Integer
Dim j As Integer
a(n) = 1
While a(n) <= 6
If n < 3 Then
Call check(n + 1, a())
Else
Cells(1, 1).Value = Cells(1, 1).Value + 1
For j = 1 To 3
Cells(Cells(1, 1).Value, j + 1).Value = a(j)
Next j
atari = 0
For j = 1 To 3
atari = atari - (a(j) = 1)
Next j
Cells(Cells(1, 1).Value, 5).Value = (atari = 0) - atari * (atari > 0)
Range("E" & Cells(1, 1).Value).Select
End If
a(n) = a(n) + 1
Wend
End Sub
Private Function strr(ByVal n As Integer)
strr = Right(Str(n), Len(Str(n)) - 1)
End Function
さらに次の実験用マクロも作ってみました.
かける条件として,
最初の所持金1万円.
所持金以内の任意の金額を,任意の目にかける.
全部で10回かける.ただし所持金が0円になった時点で終わる.
所持金が100円以下になったら,やけになって全額かける.
としてみました.常識的な範囲だと思います.
この実験を1000回試みたところ,儲かった場合もありますが,平均では所持金が1万円以下に減っていました.やはりかけない方がいいのでしょう.
でもスリルを味わいたい人にはちょうどいいかも.
Option Explicit
Const KAKERUKAISUU As Integer = 10
Const SAISHONOSHOJIKIN As Long = 10000
Sub Macro2()
Sheets("Sheet2").Select
Dim kakekin As Long
Dim shojikin As Long
Dim saikoro(3) As Integer
Dim atari As Integer
Dim shikoukaisuu As Long
Dim kaisuu As Long
Dim j1 As Integer
Dim j2 As Integer
Do
shikoukaisuu = Val(InputBox("試行回数=", "入力", 1000))
Loop While shikoukaisuu < 1
Randomize Timer
For kaisuu = 1 To shikoukaisuu
shojikin = SAISHONOSHOJIKIN
j1 = 0
While shojikin > 0 And j1 < KAKERUKAISUU
j1 = j1 + 1
If shojikin <= 100 Then
kakekin = shojikin
Else
kakekin = Int(Rnd * (shojikin - 100)) + 100 + 1
End If
shojikin = shojikin - kakekin
For j2 = 0 To 3
saikoro(j2) = Int(Rnd * 6) + 1
Next j2
atari = 0
For j2 = 1 To 3
atari = atari - (saikoro(0) = saikoro(j2))
Next j2
shojikin = shojikin + kakekin * (atari + 1) * Sgn(atari)
Cells(kaisuu, j1 + 2).Value = shojikin
Wend
For j2 = j1 + 1 To 10
Cells(kaisuu, j2 + 2).Value = ""
Next j2
Cells(kaisuu, 1).Value = shojikin
Range("A" & kaisuu).Select
Next kaisuu
Cells(shikoukaisuu + 1, 1).Value = "=AVERAGE(A1:A" & shikoukaisuu & ")"
Range("A" & (shikoukaisuu + 1)).Select
End Sub

(ペンネ−ム:杖のおじさん)
「確率をX1、X2、X3として、その事柄がおこることによって得られる値 Y1、Y2、Y3とすると
期待値=X1・Y1+X2・Y2+X3・Y3
となります。期待値が1未満の場合は、このさいころ遊びには参加しない方が良いことになります。」
3つのさいころの内1つのさいころだけ自分の数字が出る確率は、
(1/6)・(5/6)・(5/6)・3=75/216
3つのさいころの内2つのさいころだけ自分の数字が出る確率は、
(1/6)・(1/6)・(5/6)・3=15/216
3つのさいころ全部に自分の数字が出る確率は、
(1/6)・(1/6)・(1/6)=1/216
賭金を払ってそれが戻ってくる期待値は
(75/216)・2+(15/216)・3+(1/216)・4=199/216=0.921・・・
従って1未満のため、さいころ遊びには参加いたしません。
報酬の考え方で判断すると3つのさいころに1つも自分の数字が出ない時は
賭金を巻き上げられてしまいますので次の式が成り立ち、
報酬がマイナスになれば参加いたしません。報酬の期待値は、
(75/216)・1+(15/216)・2+(1/216)・3+(125/216)・(-1)=ー17/216=-0.0787・・・
従ってマイナスになるので、さいころ遊びには参加いたしません。

(ペンネ−ム:暇人)
1回さいころを振るとき自分の数字が出る確率は 1/6
1回さいころを振るとき自分と異なる数字が出る確率は 5/6である。
3回さいころを振るとき

(ペンネ−ム:Toru Fukatsu)
答え 参加しない。
| 一枚一致する確率は | 1/6 x 5/6 x 5/6 x 3 | = 75/216 |
| 二枚一致する確率は | 1/6 x 1/6 x 5/6 x 3 | = 15/216 |
| 三枚一致する確率は | 1/6 x 1/6 x 1/6 | = 1/216 |
| 全て一致しない確率は | 5/6 x 5/6 x 5/6 | =125/216 |

(ペンネ−ム:小学名探偵)
結論 長くゲームをすると損しそうなので、参加しません。
解き方
3つのサイコロの目の出方は、6*6*6通り・・・・・・・・・・・・・・・・216通り
1つのサイコロだけに自分の数字が出る場合は、5*5*3通り・・・75通り
2つのサイコロに自分の数字が出る場合は、5*3通り・・・・・・・・・・15通り
3つのサイコロ全部に、自分の数字が出る場合は、・・・・・・・・・・・・・・1通り
3つともはずれの場合は、5*5*5通り・・・・・・・・・・・・・・・・・・・・125通り
| 損得の乗数 | 損得 |
|---|---|
| 1 | 75 |
| 2 | 30 |
| 3 | 3 |
| -1 | -125 |
| ―――― | |
| 合計 | -17 |
損得の乗数は、順番に1、2、3、-1だから損得の合計=75+30+3-125=-17
つまり損です。
サイコロの出る目によって、出現率(確率)が違うとどうなるのでしょう?
例えば、
| サイコロの目 | 1 | 6 | 2 | 5 | 3 | 4 |
|---|---|---|---|---|---|---|
| 出現率×6 | 1+a | 1-a | 1 | 1 | 1 | 1 |
元の問題は、サイコロの2つや3つが当たった時の褒美が少なすぎると思いました。

(ペンネ−ム:yokodon)
僕は賭事は嫌いなので、どんなことがあっても参加しません。…しかし、これでは
数学にならないので、一応きちんと、1円をかけたときの、勝って手に入れることの
出来るお金の期待値を計算してみます。さいころには如何様がないものとして考えま
す。
6個のマス目のうち k (k = 1,..., 6)を選ぶ確率は 1/6 。
以下、さいころを3個振って、k の目が出る個数で場合分けします。
0個である確率は、(5/6)3
1個である確率は、3×(1/6)・(5/6)2
2個である確率は、3×(1/6)2・(5/6)
3個である確率は、(1/6)3
・・・と言うわけで、2項分布ですね。
出た目が k の時に1円かけて、手に入れることの出来るお金の期待値 e(k) は、
| e(k) | = 1/6 × {(-1)×(5/6)3 + 1×3×(1/6)・(5/6)2 + 2×3×(1/6)2・(5/6) + 3×(1/6)3} |
| = 1/6 × (-17/216) |

(ペンネ−ム:モルモット大臣)
期待値の問題として解法を考えました。
1〜6までの任意の整数Xにお金を掛けるとして
Xが1回だけ出る確率は(1/6)×(5/6)×(5/6)×3C1=75/216----(1)
Xが2回だけ出る確率は(1/6)×(1/6)×(5/6)×3C2=15/216----(2)
Xが3回とも出る確率は(1/6)×(1/6)×(1/6)×3C3=1/216-----(3)
Xが1回も出ない確率は(5/6)×(5/6)×(5/6)=125/216-----(4)
掛ける元金をYとすると題意より所持金からお金が増える場合の期待値は
(1)〜(4)より
Y×(75/216)+ 2Y×(15/216)+3Y×(1/216)-Y×(125/216)= -(17/216)Y
よって数学的には毎回この掛けをすることにより元金の17/216ずつ減っていくことに
なります。長くやれば絶対損ですね。
でもギャンブルは必ずリスクを伴うものですからこの程度なら宝くじよりも随分配当
が良くお得なのでやってみる価値はあるかも?

(ペンネ−ム:片松 祐司)
| 通り数 | お金の増減 | 期待値 | |
|---|---|---|---|
| 3個当たり | 1 | 3 | 3/216 |
| 2個当たり | 15 | 2 | 30/216 |
| 1個当たり | 75 | 1 | 75/216 |
| ハズレ | 125 | -1 | -125/216 |
| 計 | 216 | − | -17/216 |
期待値 -17/216 で胴元有利。
# 間違っていたら…恥ずかしいなぁ〜と思っていたら
# 計算間違いで小島さんから赤ペンが入って帰ってきた(^_^;;;;
# 上記は修正済み
ポン!(手をたたく音) そうか!
1度目は計算間違いしていて気付かなかったけど
| 通り数 | お金の増減 | 期待値 | |
|---|---|---|---|
| 3個当たり | 1 | 5 | 5/216 |
| 2個当たり | 15 | 3 | 45/216 |
| 1個当たり | 75 | 1 | 75/216 |
| ハズレ | 125 | -1 | -125/216 |
| 計 | 216 | − | 0/216 |
とすれば期待値 0 ですね!
・2個当たりを3倍+元金返し
・3個当たりを5倍+元金返し
にしてもらえば公平な(?)賭けになるかも…

(ペンネ−ム:大熊猫大王)
aという数字にかけたとする。
aにぞろ目になる確率は216分の1でそのときの利益は3。
aに二つ出る確率は216分の15でそのときの利益は2。
aには一つしか出ない確率は216分の75でそのときの利益は1。
aに一つも出ない確率は216分の125でそのときの利益はー1。
よって期待値を計算すると-17/216となり、平均すれば損になる。
でも、わたしだったらこの程度の損なら楽しみのために必要な経費と考え賭けに参加する。
また、もし同時に二つかけていいのなら期待値は+228/216となるので
いかさまとわかっていない限り必ず参加する。

(ペンネ−ム:15KARATSOUL)
私なら参加しません。
nの目にx円かけたとします。(1≦n≦6,nは整数)
3個のさいころを同時に投げたとき,
3個とも当たる確率は,
(1/6)3=1/216.
2個当たる確率は,
3C1×(1/6)2×5/6=15/216.
1個だけ当たる確率は,
3C1×1/6×(5/6)2=75/216.
全部はずれる確率は,
(5/6)2=125/216.
よって,儲かる金額の期待値は,
3x・(1/216)+2x・(15/216)+x・(75/216)−x・(125/216)=−(17/216)・x(円).
です。長い目で見ると損をしますね。
儲けた時点でやめるのがよいでしょう。
…あ,賭け事じゃあ当たり前かな?(苦笑)
この賭け事はチャカラックかな?

(ペンネ−ム:teki)
答え
遊びで少額のお金を使うのなら、まぁ許せる範囲ですが
全財産賭けてやる気は毛頭ありません。
理由:
このゲームの期待値を計算します。
期待値は、
2×3C1×5/6×5/6×1/6+3×3C2×5/6×1/6×1/6+4×1/6×1/6×1/6=199/216
となり、1未満です。
従って、このゲームは長くやればやるほど、賭けた側が損をするゲームです。
その損の割合は、1-199/216=17/216 と計算でき、1回やる毎に17/216だけ損
をします。
従って、遊びで少額のお金を使うのは許せるとしても、全財産賭けてやるのは
愚の骨頂と言えます。
もっとわかりやすく説明すると、以下のようになります。
今、仮に6つの数字に同額の金額を賭けたとします。(実際には、こんなこと
をする人はいないでしょうが)すると、次の3つのケースが考えられます。
1 サイコロの目が3つとも違う場合
3ヶ所小当たりで、3ヶ所はずれ→賭け金6に対して、配当2×3=6→
損得無し
2 サイコロの目が2つ同じで1つが違う場合
1ヶ所中当たりで、1ヶ所小当たり→賭け金6に対して、配当3+2=5
→差引1の損
3 サイコロの目が3つとも同じ場合
1ヶ所大当たりで、5ヶ所はずれ→賭け金6に対して、配当4→差引2の
損
つまり、1のケースを除いては、賭けた側が損をすることになります。
<備考1>
このゲームを、客と胴元がイーブンになるようにするためには、配当を次の
ように変更する必要があります。
1 1つのサイコロの目が当たった場合・・・配当2倍(問題の設定どおり)
2 2つのサイコロの目が当たった場合・・・配当4倍(賭け金+3倍)
3 3つのサイコロの目が当たった場合・・・配当6倍(賭け金+5倍)
このように設定すると、長い目で見れば損得無しになるのですが、これでは
胴元の儲けは0となるので、商売になりませんね。
そこで、私なら次のように設定します。
1 1つのサイコロの目が当たった場合・・・配当2倍(問題の設定どおり)
2 2つのサイコロの目が当たった場合・・・配当3倍(賭け金+2倍)
3 3つのサイコロの目が当たった場合・・・配当10倍(賭け金+9倍)
この設定、一般のギャンブルではよく使われている設定で、大当たりの倍率を上げる
ことにより、客側に「もしかしたら、大金が手に入るぞ!!」という気持ちを誘発させて、
多くの客を集めることができます。
また、2のケース以外は、客側が儲かることになるので、実際の期待値を計
算して見ない限り、客側は「この設定なら有利ではないか?」と錯覚させることがで
きます。
この設定でも、胴元は11/216=約5%の利益を得ることができます。
このような設定は、実際に宝くじ等で一般的に採用されています。
<備考2>
一般的にギャンブルにおける胴元の取り分を「ハウスアドバンテージ」と言
いますが、このゲームのハウスアドバンテージは、17/216=約8%と計算できます。
つまり、1回のゲームで100円賭けた場合の胴元の儲けは、約8円と計算できるのです。
世の中で実際行われているギャンブルのハウスアドバンテージは、大体次のように
設定されています。
| クラップス(サイコロゲームの1種) | :2〜12%(賭け方による) |
| ルーレット | :5% |
| 競馬・競輪 | :25% |
| 宝くじ | :約40% |
| パチンコ | :???% |

(ペンネ−ム:kirkland)
| 先生 | 「今回は小6の君にはムリだろう。期待値どころか順列・組み合わせも知らないんだろう?」 |
| A君 | 「そんな変なモノを使わなくてもできますよ!屁みたいなもんですな。はははっ〜!僕は、理科が得意なんだもーん!」 |
| 先生 | 「小島先生に褒められて調子に乗ってるんじゃないっ!」 |
| A君 | 「そもそも、賭け事は小学校で禁止されているので、やらない方がいいと思いま〜す。」 |
| 先生 | 「まじめに考えなさい!まず、サイコロを3つ振ったとき、目の出方は全部で何通りあるのか分かる?」 |
| A君 | 「九九ぐらい知ってますよ。サイコロ1個は6通りの目があるので、3個では6×3で18通り!」 |
| 先生 | 「これでは先が思いやられるなぁ。1個目のサイコロの目の出方は6通りで、2個目は1個目の6通りのそれぞれに対
して6通りずつあり、3個目も同様なので、6×6×6=216通りだ。」 |
| A君 | 「あっそうか。じゃあ216回やれば、理屈の上では1回ずつ出てきますね。」 |
| 先生 | 「その通り。さぁ、実際にやりながら考えていこうか。私が胴元をやってあげよう。」 |
| A君 | 「じゃあ、気合いを入れて1万円ずつ賭けていきますから、先生、ちゃんと支払って下さいよ。あの家、抵当に入れておいた方がいいですよ〜。うーんと、何に賭けようかな?ラッキーセブンの7!」 |
| 先生 | 「殴っていい?サイコロなんだから7なんかねえだろうよ!第一、216万円も持ってないだろ!」 |
| A君 | 「ギャグですよ。先生、そんなに怒らなくても。まったく、大人げないんだからぁ。小学生らしく1円ずつにしますよ。 ナンバーワンの1にしますね。1が3つ出るのは(1,1,1)の1通り。ピンゾロは5倍付けですよね?」 |
| 先生 | 「それは、チンチロリンのルールだろ!問題文ぐらいちゃんと読みなさい。」 |
| A君 | 「残念。賭け金も含めて4円だけ戻ってきますね。先生、払って下さい。1が2つ出るのは、(1,1,2)、(1,1,3)、…、(1,1,5)の5通りですか?」 |
| 先生 | 「(2,1,1)でもいいんじゃないの?」 |
| A君 | 「あっそうか、(1,1,2)、(1,2,1)、(2,1,1)の3通りずつあるのか。全部で5×3=15通りですね。これで45円ゲット!早くくださいよ!」 |
| 先生 | 「あとは、1が1つだけ出るものを考えればいいんだけど、ちょっと難しいかも。」 |
| A君 | 「楽勝、楽勝!(1,2,2)のパターンは3通りあるし、(1,2,3)のパターンは…、もっと多い気がします。6通りですか?げげっ、けっこう面倒臭いですね。」 |
| 先生 | 「直接考えにくかったら、1が1個も出ないときを考えれば?」 |
| A君 | 「1個目は2,3,…,6の5通り、2個目、3個目も5通りずつだから、5×5×5=125通りです。125円も取られちゃうのか。全体の216通りを求めたのと同じ考え方でいいわけですね。というわけで、1が1つだけ出るのは、216−1−15−125=75通りですね。150円ゲット!超ラッキー!ジュースが買えるぞ!」 |
| 先生 | 「まぁ、直接求めると、5×5×3=75でいいんだけどね。」 |
| A君 | 「さあて、合計、合計っと。4+45+150=199円!!(絶句)先生、お金返して下さいよーぉ。お母さんに怒られちゃいます〜ぅ。(泣)」 |
| 先生 | 「まぁ、それが大人の世界ってモンだ。授業料だと思って諦めなさい。」 |
| A君 | 「この極悪教師!!よ〜し!明日、友人のB君をだましてお金を巻き上げてやろう!」 |
| 小島 | (特別出演) A君! そんなことをしては絶対にだめですよ、先生に怒られてしまいますからね。 |

(ペンネ−ム:柿本 浩)
これは「期待値」を求めてみろ、って事なんでしょうね。
※サイコロ:A・B・C
賭けた数字とサイコロの目が一致する事:当たり
サイコロの目と異なる事:はずれ とそれぞれ表現します
<プレイヤーの立場で考えた場合>
<胴元の立場で考えた場合>
各パターンの確率は、もちろんプレイヤーの場合と同じだが、
胴元の立場で得られる結果を考えると
※胴元は最初に賭け金を支払う訳ではないので 賭けを行う度に、賭け金の0.08倍の金額を得る事が期待される。
※胴元の期待値は 1 − (プレイヤーの期待値(199/216)) でも計算できる。
ただし、問題文の問いかけは
「あなたはこのさいころ遊びに参加しますか?」であるため・・・
解.「もちろん参加しますよ!! ・・・胴元として」
これが、私の中での正解である。
〜〜〜〜〜〜〜〜
この数値だけ見ると、「何だ、参加するだけプレイヤーの損じゃんか!」
と思われるかもしれませんが、一般的な宝くじのデータでは
1枚300円に対して、戻ってくる期待値は100 〜 150円程度です。↓
LOTOの遊舎/期待値
数学で雑学 ≫ 数学関連小ネタ集 ≫ 宝くじの期待値
キューピーランド準備室/宝くじの期待値
An easy lecture of Math./宝くじに託す夢
0.5倍以下、半額以下しか期待できないんですよ?
それに比べりゃ、はるかに効率は良いと思いますけどね。
基本的にギャンブルなんて全部、胴元の方が儲かるようになってるんですから。

(ペンネ−ム:高橋 道広)
答え やらないっ。
小学生の答え
ぼくわ そーいうものわ やらないほうがいいとおもいます。
だって お母さんは いつも おまつりの時に ぼくに
そーいうことお してる人は もうかるから してるんだ。
きおつけよう あまいことばと かあにばる とおしえて
くれてるから です。
高校生の答え
これは期待値ですね。期待値が賭ける金額より大きければ参加したほうが
いいと(なぜかよくわからないけど)授業で習いました。
掛け金を1とします。
2倍になる確率 1/6×5/6×5/6×3=75/216
3倍になる確率 1/6×1/6×5/6×3=15/216
4倍になる確率 1/6×1/6×1/6=1/216
期待値は75/216×2+15/216×3+1/216×4=199/216
ですからこの遊びには参加しないほうがよさそうです。
酔っ払いのおじさんの答え
てやんでぃ 人生 ギャンブルでぃっ。競馬もパチンコも
胴元が儲かるようにできてるってことなんざあ なからしってらあ。
博打をしないなんて つまらんぜぃ。こちとら蝦夷っ子(えぞっこ)でいっ。
男なら どーんと行かなきゃ どーんと。へんっ。
ずりずりっ(手の平を上に向けて手のひらの付け根で鼻をすする効果音)

| Banyanyan | teki | 小学名探偵 |
| 柿本 浩 | 浜田 明巳 | 15KARATSOUL |
| モルモット大臣 | 夜ふかしのつらいおじさん | kiyo |
| やなせ | Toru Fukatsu | 理一郎坊ちゃん |
| 大熊猫大王 | こざっぱ | TAKE |
| 高橋 道広 | スモークマン | サダちゃん |
| 杖のおじさん | かつ | 三角定規 |
| 片松 祐司 | 暇人 | yokodon |
| kirkland |

期待値を計算していただくと、199/216になりますね。 ただし、賭け金を払う前の段階を基準のとると、 報酬は、「1倍、2倍、3倍、−1倍」であることに注意していただいて、-17/216となります。 どちらの基準でもよろしいかと思います。 要は、長く続ければ続けるほど、ほぼ確実に損をするということです。
今回の問題の設問は、「さあ、あなたはこのさいころ遊びに参加しますか?」ですから、この計算をもとにそれぞれ判断をしていただければいいわけです。実際、いただいた解答は「私は基本的にギャンブルはしない。」から、「この程度の損ならもちろん賭けますよ。」まで様々ですね。 私自身はほとんどギャンブルはしませんが、実は「胴元になりたい!」、柿本浩さんと同じです。でも、kirklandさんの解答に出てくるA君を注意してしまった手前、そういうわけにもいかないかなあ・・・。
このゲームは、15KARATSOULさんがご紹介くださったように、「チャカラック」というものだそうですが、賭け方を変えてみたらどうなるかという考察を何人かの方からいただきました。どうしたら損をしない(期待値が1)かという方向と、どうしたらもっともらしく見せかけて胴元がたくさん儲けられる(期待値を下げる)かという方向があるように思います。
後者についていえば、あまり儲かりそうにないけれど、一発当たれば大きいぞという印象を持たせることが肝要かと、宝くじ(多空くじ?)を見て思いますね。 期待値が半分にも持たないのに、あれほど売れるとは・・・。(年末ジャンボ、お買いになりましたか?)
tekiさん、柿本浩さん、資料提供どうもありがとうございます。
高橋道広さんの解答、サイコーです。
関連して → コロキウム室 NO.1334 問題71に関して

 E-mail
E-mail
 戻る
戻る
 top
top