Weekend Mathematics/コロキウム室/NO.159
コロキウム室
| NO.1334
| 2002.12.2. | おいたん | 問題71に関して
|
11月分の問題71
では、期待収益と掛金の大小を比較して結論を出していました。では次のようなゲームの場合はどうでしょう。
コインを表が出るまで投げつづける。n回目で表がでたら2n円もらえる。表がでた時点で終了する。このゲームへの参加費がいくらならあなたは参加するか?
みなさん、いくらぐらいなら払いますか?きっと、1円とかせいぜい2円くらいでしょうね。でも期待収益Xは
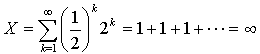
となり、とってもおいしいゲームのはずなんですが。
これはSt. PetersburgのParadoxという有名な問題で、こうしたゲームの参加の是非を判断するには、期待収益そのものではなく、収益から得られる期待効用と掛け金をセーブすることの期待効用の大小を比較する必要があります。通常は、期待効用は収益が大きければ大きくなりますが、その増加率は逓減します。同じ100円の増加でも、1円が101円になるときのほうが、10万円が10万100円になるときのほうよりうれしいですよね。そうすると、期待効用は、たとえばルートやログのような形の関数になります。
上記の例で、たとえばx円から得られる期待効用が 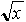 としましょう。すると、期待効用E(X)は
としましょう。すると、期待効用E(X)は
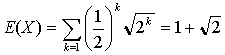
となり、掛金yをセーブして得られる効用 を比較して、
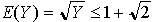
となるYに対してのみ、参加するインセンティブが生じます。この場合のYは 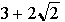 円、つまり6円弱ですね。
円、つまり6円弱ですね。
今回の問題で、期待収益と掛金の大小によってさほど違和感のない結論が導き出せたのは、扱う金額が小額かつ近傍に集まっていて、期待収益を と線形に近似化しても無理がないようなケースだったからでしょう。

| NO.1335
| 2002.12.7. | 中川 幸一 | 自然数の分割(2)
|
(4) 区別のつかない6n個のボールを, 区別のつかない3個の箱に入れる場合の数と同じで, 96年・東大後期に本問とは別の誘導つきで出ています.
n を正の整数とし, n 個のボールを 3 つの箱に分けて入れる問題を考える。ただし, 1 個のボールも入らない箱があってもよいものとする。以下に述べる 4 つの場合について, それぞれ相異なる入れ方の総数を求めたい。
(1) 1 から n まで異なる番号のついた n 個のボールを, A, B, C と区別された 3 つの箱に入れる場合, その入れ方は全部で何通りあるか。
(2) 互に区別のつかない n 個のボールを, A, B, C と区別された 3 つの箱に入れる場合, その入れ方は全部で何通りあるか。
(3) 1 から n まで異なる番号のついた n 個のボールを, 区別のつかない 3 つの箱に入れる場合, その入れ方は全部で何通りあるか。
(4) n が 6 の倍数 6m であるとき, n 個の互に区別のつかないボールを, 区別のつかない 3 つの箱に入れる場合, その入れ方は全部で何通りあるか。

| NO.1336
| 2002.12.7. | かつ | ガウスの発散定理の応用(4)
|
DDTさんが曲面論についてお話をしていたので多少補足してみたいと思います。
曲面の状態を考えるときに外的なことは必要ないのはそのとおりですが、もう
ちょっと詳しく説明してみたいと思います。
曲面に座標系を作る事というのは多様体の定義です。曲面上に格子点を作り局所
的に平面座標に落として考ようと考えるからです。
そこで、曲面は曲がったりしているわけですから局所的に格子点を作るだけでは
何も理解できません。そこで曲がり具合というのを調べることにしました。それ
がガウス曲率と呼ばれるものです。はじめガウス曲率は高さ(平面座標に落とし
たとしても高さが必要、これが外的性質)が必要だとしたのです。しかしなが
ら、このガウス曲率を調べると外的性質(高さ)を必要としない局所座標内の接
ベクトルによって表現することができました。これにはガウスも驚いたそうで
す。なのでこれは「ガウスの驚異の定理」とも呼ばれています。これによって、
たとえばこの地球が球状だということをスペースシャトルや人工衛星などを使わ
なくても地球上にいて理解できるのです。
なんだか文章で書いてしまったのでわかりにくくてすみません。
ちょっと解釈がDDTさんと違うかもしれませんがそのところはご容赦ください。

| NO.1337
| 2002.12.10. | 物理君 | 光の振幅
|
問1
光源からの光波(球面波)が直接観測点Pに到達する場合と回折して到達した光波の振幅を比較し、回折光の位相がπ/2ずれることを確かめよ。
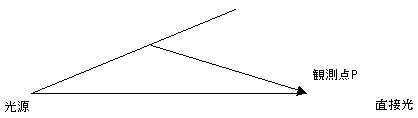
回折光は直接光を底辺とする三角形の頂点あたりになります。
問2
Zone Plateの1番目および2番目のみの光を通すようなピンボールを置いたとき観測点Pでの光の振幅が0になることを示せ。
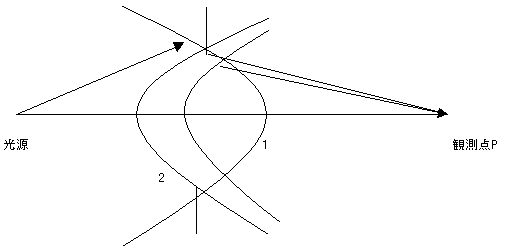

| NO.1338
| 2002.12.15. | 水の流れ | 条件つき自然数
|
第110回数学的な応募問題
太郎さんは、生徒と一緒に大学入試問題を眺めていたところ、東京大学に出ていた次のような問題をみつけました。そこで、アレンジして出題しましたから、皆さん、チャレンジください。
次の条件を満たす正の整数全体の集合をSとおく。
「各桁の数字は互いに異なり、どの2つの桁の数字の和も9にならない。」
ただし、Sの要素は10進数で表す。
また、1桁の正の整数はSに含まれるとする。
(1)Sの要素でちょうど1桁のものは何個あるか。
(2)Sの要素でちょうど2桁のものは何個あるか。
(3)Sの要素でちょうど3桁のものは何個あるか。
(4)Sの要素でちょうど4桁のものは何個あるか。
(5)Sの要素でちょうど5桁のものは何個あるか。
(6)Sの要素で小さい方から数えて2003番目の要素を求めよ。

| NO.1339
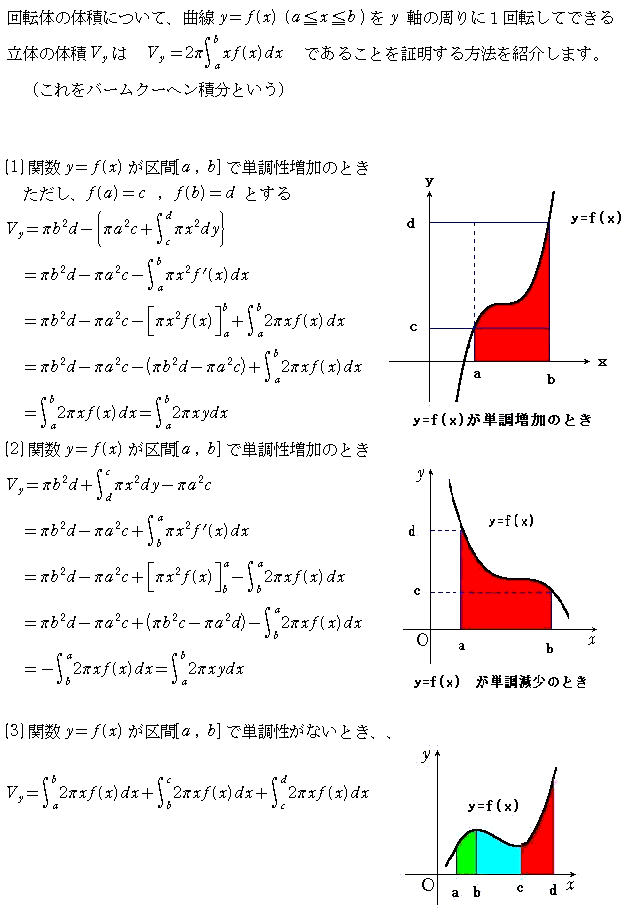
| 2002.12.15. | 水の流れ | バームクーヘン積分
|

 E-mail
E-mail
 戻る
戻る
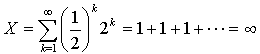
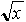 としましょう。すると、期待効用E(X)は
としましょう。すると、期待効用E(X)は
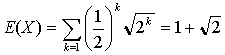
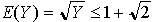
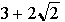 円、つまり6円弱ですね。
円、つまり6円弱ですね。



 E-mail
E-mail
 戻る
戻る