6.間違い探しの問題
(1)「2=3である。」
4−10と9−15はどちらも−6となり、等しい。
この各々に同じ数25/4を加えても等しいから
4−10+25/4=9−15+25/4
この両辺を因数分解すると
(2−5/2)2=(3−5/2)2
となり、
2−5/2=3−5/2
∴2=3
さて、この証明の誤りを見つけてください。
(2)「64=65である。」
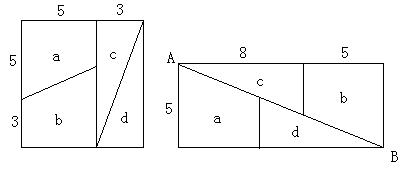
1辺が8の正方形を下の図のように4つの部分に切り、 これらの部分で長方形を作る。 この長方形の横の長さは13、縦の長さは5となる。
最初の正方形の面積は、8×8=64 であるのに、 これから作られた長方形の面積は 13×5=65 となる。
つまり、64=65である。これはどうしたことでしょうか?
問題の出典
「数学ふしぎ・ふしぎ」
矢野健太郎
新潮文庫
答えと解説
(1)回答・その1
(ペンネ−ム:凡人)
(2-5/2)2=(3-5/2)2となり、
2-5/2=3-5/2というところがあるが、
これは(2-5/2)2=a2、
(3-5/2)2=b2とおくと、
a2=b2のとき、a=bのときを考えているが、
-a=-bのときもあるので、
この場合も考えなければいけないので、ここが誤りだと思います。
(1)回答・その1・コメント
a=bと-a=-bは結局同じことです。
彼がいいたいのはaとbが同符号か異符号か両方の可能性があるということなのでしょうね。
(1)回答・その2
(ペンネ−ム:BABY MINNIE)
4-10と9-15はどちらも-6になる。
この各々に25/4を加えても等しい。
4-10+25/4=9-15+25/4を因数分解したら、
(2-5/2)2=(3-5/2)2になる。
しかし、この( )をいっぺんにははずせない。
例えば、2-5/2をxとおくと、x2=(3-5/2)2となる。
x2=4などの式を参考にすれば、x=±2である。
つまり、x2=(3-5/2)2は、x=±(3-5/2)ということになる。
この結果からもわかるようにxの値はこの方法でやると、+なのか−なのかわからない。
(1)回答・その3
(ペンネ−ム:MK142857 )
(2-5/2)の2乗=(3-5/2)の2乗から(2-5/2)=(3-5/2)を導き出したところが間違いです。
一般にAの2乗=Bの2乗 とA=Bは同値ではないからです。
(2)回答・その1
(ペンネ−ム:es)
面積が変わってしまうのは、aとdの斜辺の傾きが違うから。
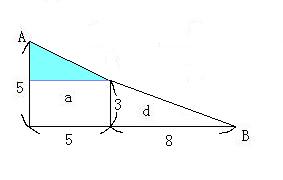
もし、正方形と長方形の面積が等しいなら、 ブル−の三角形とdの三角形は相似であるはず。
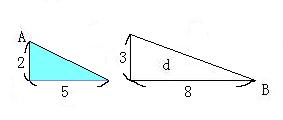
しかしながら辺の比が一方では2:5、もう一方は3:8となっているので、 相似ではない。
だから、aとdの斜辺の傾きが違う。
(2)回答・その2
(ペンネ−ム:コレクトコ−ルは106番!)
長方形に組み替えたあとも、
4つの部分の面積の合計は64である。
では、なぜ65になってしまうのか。
実は、長方形に組み替えるには、
少し内部にすきまができるためである。
すなわちすきまのない問題文の図は違うのである。
実際の図を示します。
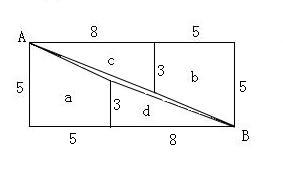
aとd、およびcとbの間に、すきまができている。
さて、4つの部分の面積をあらためて求めると、
- (aの面積)=(5+3)×5÷2=20
- (bの面積)=(5+3)×5÷2=20
- (cの面積)=3×8÷2=12
- (dの面積)=3×8÷2=12
(a、b、c、dの面積の合計)=20×2+12×2=64
(すきまの面積)=(長方形の面積)−(a、b、c、dの面積の合計)=65−64=1
と、いうわけで、64=65は誤りであり、64+1=65が正しい。(当たり前?)
P.S. この問題は、紙で実際に作ってみるまでわかりませんでした。
証拠としてその紙を同封します。いらなければ捨ててください。
(2)回答・その3
(ペンネ−ム:Ayako)
私は組み替えた時に、
長方形にならないんじゃないかと
考えました。
・・・で、実際にやってみると、
(コメント:折り紙で作ったものが張り付けてありました。)
う−ん・・・なるような、ならないような。
角Bがあやしいような・・・。
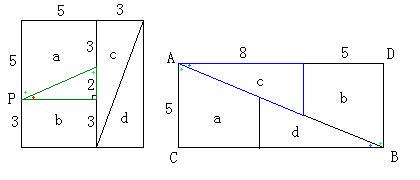
点Pから右の辺に垂線をひいて直角を作る。
右の図が長方形になる(角Bが直角になる)ということは、 赤い角と青い角が同じ角度であればよい。
そこで、緑の三角形と青の三角形の相似を考える。
辺の比が2:5≠3:8より、相似ではない。
従って、赤い角と青い角は同じ角にはならない。
(ちなみに私の作った図から考えると 赤い角よりも青い角の方が小さいのでは!?)
右の図の∠Aと∠Bは直角ではないので、 右の図は長方形にはならない。
13×5=65は成り立たない。
感想:あまりうまく説明できなかったけれど、
これってやりだすととまらないですね。
3時間も悩んでしまいました。
正解者(ペンネ−ム)
matheman
MK142857
しん
ちゃんた
BRAINMANIA
はなフムフム
BABY MINNIE
Ayako
Yoshimi
コレクトコ−ルは106番!
凡人
匿名希望
まとめ
- について
一般にx2=y2だからといって、 x=yとは限りません。x=-yの可能性もありますからね。
「x=yならば、x2=y2」は真(正しい)ですが、 逆、「x2=y2ならば、x=y」は必ずしも真ならず、です。
|x|=|y|も同様です。
- について
右の図形には(面積1ぶんの)すきま、 細長い平行四辺形、があるのです。

直角三角形cの斜辺の傾きは-3/8であるのに対し、 台形aの斜辺の傾きは-(5-3)/2=-2/5となり、
-2/5(-16/40)<-3/8(-15/40)
であることから、aとcの間にわずかながらすきまのあることがわかります。
さて、類題の作り方を紹介しましょう。
フィボナッチ数列というのを利用します。
1,1,2,3,5,8,13,21,34,・・・
というものです。
この数列は前の2つを足すことで3つ目の数ができています。
1+1=2、1+2=3、2+3=5、3+5=8、5+8=13・・・という具合です。
この数列において、隣り合った3つの数をa、b、cとすると、
b2=a×c±1
という性質を持っています。詳しい証明
今回の問題は、a=5、b=8、c=13として、
「82=5×13-1」を利用したものです。
a=8、b=13、c=21とすると、
「132=8×21+1」となります。
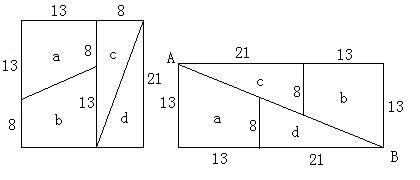
a=13、b=21、c=34として、
「212=13×34-1」を利用すると
次のような問題になります。
これを使って、「441=442?」で、誰かをだましてみましょう。
さて、今回の間違い探しはいかがでしたか?
もっともらしい説明にだまされないように、
常に疑いの目でみることも大切かもしれません。
そして、証明をみた最初に「何か変だ! どこかはわからないけれども、
でもどこかおかしい!」と感じる、その感覚が重要だと思います。
これは数学に限ったことでもないですね。

 戻る
戻る