５．カ−ドの問題
下の４枚のカ−ドから３枚を取って１列に並べ、 ３桁の整数を作ります。 この時、１とその数自身しか約数を持たない数（素数といいます。） をすべて求めよ。
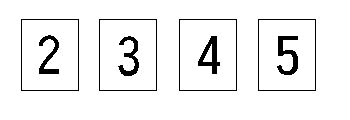
問題の出典
慶応義塾中等部'92入試
「パズルより面白い中学入試の算数」
ピ−タ−・フランクル
講談社
答えと解説
５．カ−ドの問題
下の４枚のカ−ドから３枚を取って１列に並べ、
３桁の整数を作ります。
この時、１とその数自身しか約数を持たない数（素数といいます。）
をすべて求めよ。
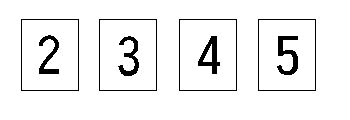
回答・その１
（ペンネ−ム：大地）
２、３、４、５の４枚のカ−ドを使ってできる３桁の数の中で、 １の位に２、４がくると２の倍数になってしまい、５だと５の倍数になってしまうので、 １の位は３でなければならない。
１の位が３の数は、２４３、２５３、４２３、４５３、５２３、５４３、 の６個。
その中で、各位の和が３の倍数だと３で割り切れてしまうので、
２４３、４２３、４５３、５４３はだめになるから、
２５３、５２３が残る。
２５３は１１で割り切れるので、素数は５２３。
回答・その２
（ペンネ−ム：はなフムフム）
下１桁が２の時、２を約数にもつので、×
下１桁が４の時、２を約数にもつので、×
下１桁が５の時、５を約数にもつので、×
よって、下１桁は、３となる。
３桁の数をａｂｃとおく。
ａｂｃの合計が３の倍数の時は、３の倍数なので、×
よって、ａｂの組み合わせは、(25)、(52)の２つ。
（２４３、４２３、４５３、５４３は３の倍数）
また、ａｂｃがａ＋ｃ＝ｂの時は１１の倍数なので×
したがって、２５３は２＋３＝５なので、×
よって、素数だと考えられる数字は５２３の１つ。
５２３に約数がないか、調べてみる。
13×11=143、 13×31=403
13×41=533、 17×19=323
17×29=493、 17×39=663
した１桁が３になる素数同志をかけてみたが、
５２３になるものはなかったので、５２３は素数。
回答・その２・コメント
５２３が素数であるという確認をしているところがいい！
正解者（ペンネ−ム）
Junji
Sin-ichi
ちゃんた
通りすがりの大学院生
ＢＲＡＩＮＭＡＮＩＡ
ＢＡＢＹ ＭＩＮＮＩＥ
サンジェルマン
石川ごえもん
コレクトコ−ルは１０６番！
くつ下
匿名希望
まとめ
次の数で割り切れるかどうかを判定する方法を示しましょう。
２・・・下１桁が偶数なら割れる
３・・・各桁の数字を足してみてそれが３で割り切れれば、割れる。
４・・・下２桁が４で割り切れれば割れる
５・・・下１桁が５か０なら割れる
６・・・２で割れて、３で割れれば、割れる
７・・・下から３桁ごとに区切り、奇数番目のものの和と、偶数番目のものの和の差が７の倍数なら割れる。
８・・・下３桁が８で割り切れれば割れる
９・・・各桁の数字を足してみてそれが９で割り切れれば、割れる。
１０・・・下１桁が０なら割れる(我ながらつまらないことかいてるなあ・・・)
１１・・・奇数桁の和と偶数桁の和の差が、１１の倍数なら割れる
１２・・・４で割れて、３で割れれば、割れる
１３・・・下から３桁ごとに区切り、奇数番目のものの和と、偶数番目のものの和の差が１３の倍数なら割れる。
これについての詳しい証明
以上をふまえると、２＋３＋４＝９、３＋４＋５＝１２より、
［２］［３］［４］、［３］［４］［５］の」組み合わせはどう並べても
必ず３の倍数になるからダメ！
［２］［４］［５］の組み合わせは下１桁が５だと５で割れるし、
２か４なら２で割れるからやはりダメ！
残りは、［２］［３］［５］の組み合わせしかない。
下１桁は５と２はだめだから３。
２５３か５２３。
２５３は１１で割れる。
５２３は割り切れる整数が見つからない。
よって素数は５２３ただ１つだけ。
寄せられたレポ−トでは、２５３＝１１×２３に気づかず、
これも素数と答えた人が多かったです。
最後に残った１つが素数かどうかもきちんと確認せず、
答えているレポ−トもちょっと気になります。
もしかしたら、「該当なし」が正解かもしれませんからね。
きちんと確認しましょう。
それでは、ある数Ｎが素数かどうか？ どうやって判定したらよいでしょうか。
詳しくはこちら
質問
しかし、大きな数が素数であることを確認する有効なチェック法はないのかなぁ？
お答えします
ありません。
たとえば、２以外の偶数は当然素数ではないわけだし、 何か１つでも素因数分解が見つかればそれは素数ではないことが判明します。
しかしながら、ある数が素数であることを示す方法は「これっ！」というものがありません。
「エラトステネスのふるい」にかけるしかないでしょうね。
これは２、３、５、７、１１、１３、１７・・・と素数で順番に割っていってＮの約数を探すのです。
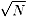まで探して見つからなければＮは素数です。
なぜ、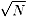まで探せば充分なのでしょうか？
約数は必ずペアがいるからです。もし、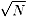を越えたところに約数がみつかったなら
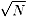実はそのパ−トナ−がより前にいたはずですよね。
だから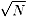までで充分なのです。
素数に関する話
１．素数は無限に存在する。
背理法（結論を否定して、矛盾を導き出す証明方法）による。
素数が有限個だとして、最大の素数をｐとする。
すべての素数の積に１をたしたものをＮとする。
Ｎ＝２・３・５・・・・ｐ＋１とおく。
Ｎ＞ｐより、Ｎは素数ではない。
ところがＮはどんな素数で割っても割り切れない。（余りが１）
従って、Ｎは素数である。これは矛盾。
ゆえに、素数は無限に存在する。
２．双子素数は無限に存在するだろうか？
双子素数・・・３と５、１０１と１０３の様に差が２である素数のペア。
私の手元にある資料によれば、知られている最大のペアは７６×３１３９−１と７６×３１３９＋１だそうです。
双子素数は無限に存在すると考えられてはいるが、まだ証明されてはいません。
３．すべての偶数（≧４）は、２つの素数の和として表せる。（ゴルドバッハの推測）
４＝２＋２
６＝３＋３
８＝３＋５
１０＝３＋７＝５＋５
１２＝５＋７
のように、３３×１０６以下の偶数については実際の計算によって確認されています。
しかしながら、すべての偶数について証明されているわけではありません。
４．ｘ以下の素数の個数をπ(ｘ)とすると、ｘが十分大きいとき、
π(ｘ)≒ｘ／ｌｏｇｘ（素数定理）
すべての素数を与える公式は存在せず、その配置はきわめて不規則です。
にも関わらず、素数の大きな区画を調べてみると、
素数の平均的な配置はきわめて規則的だということです。
これはすごいことだと思いません？
１９世紀初め、ガウスとラグランジェはπ(ｘ)とｘ／ｌｏｇｘの表をみて、大きいｘに対して
π(ｘ)／(ｘ／ｌｏｇｘ)の比がほぼ１に等しいとそれぞれ独立に考えたのだけれども、
証明はできませんでした。
１８５１年、ロシアの数学者チェビシェフは、極限値が存在するとすれば、
それは１であるということを証明したのだけれども、極限値の存在そのものは証明できませんでした。
最終的には１８９６年、J.HadamardとC.J.de la Vallee Poussinによってそれぞれ独立に
しかもほとんど同時に証明されました。
それにしても、こんなところに対数logが登場するというのも不思議ですねえ！
数学の神秘を感じます。
戻る